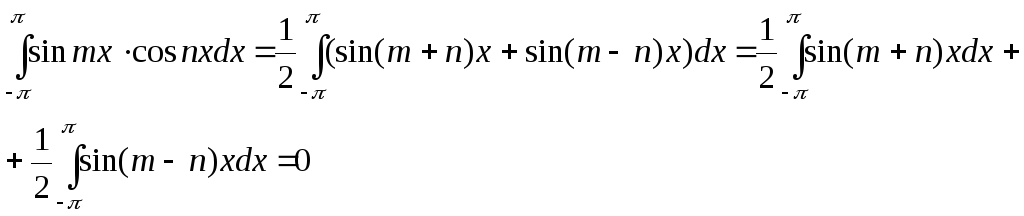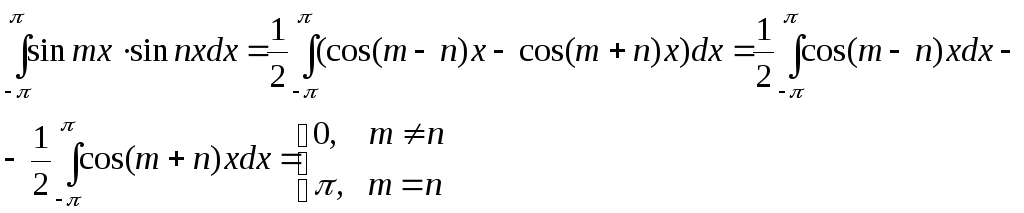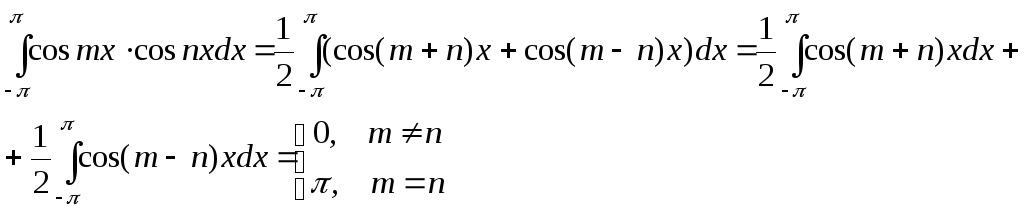5. Ряды фурье

5.1 Периодические функции и процессы

В различных технических процессах часто приходится рассматривать явления, которые периодически повторяются через определенный промежуток времени.

Процессы, которые повторяются через определенный промежуток времени называютсяпериодическими.Примерами периодических процессов могут служить движения шатуна и поршня в двигателях, явления, связанные с распространением электромагнитных колебаний и многие другие. Периодические процессы встречаются в радиотехнике, теории и практике автоматического регулирования, теории упругости и др.

Изучение периодических процессов математически описывается периодическими функциями, т.е. величины, характеризующие такой периодический процесс, являются периодическими функциями от времени f(t).

Определение. Периодической функциейназывается функцияf(x) , определенная на множествеD, и имеющая период, т.е. при каждомвыполняется равенство.

Для построения графика периодической функции с периодом Т достаточно построить его на любом отрезке длинойТи периодически продолжить его на всю область определения.

Основные свойства периодической функции:

1. Алгебраическая сумма периодических функций, имеющих один и тот же период Т, есть периодическая функция с периодомТ.

2. Если функция f(x) имеет периодТ, то функцияf(аx)имеет период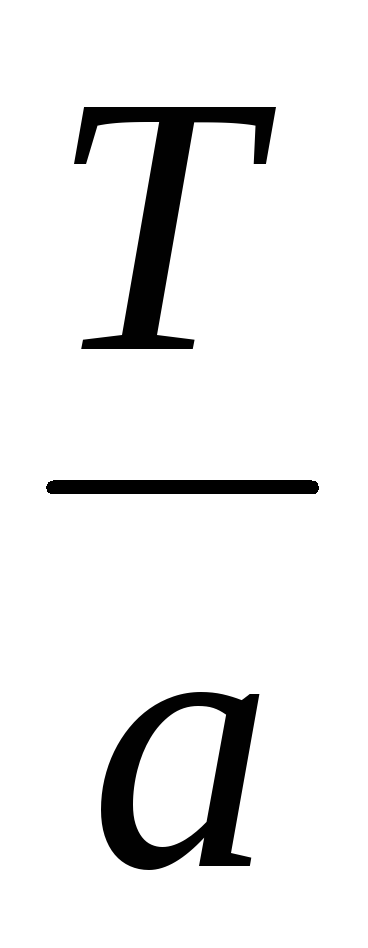; действительно.

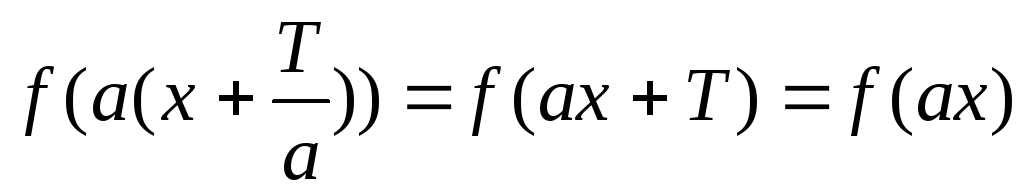3. Если функция f(x) имеет периодТи интегрируема на отрезке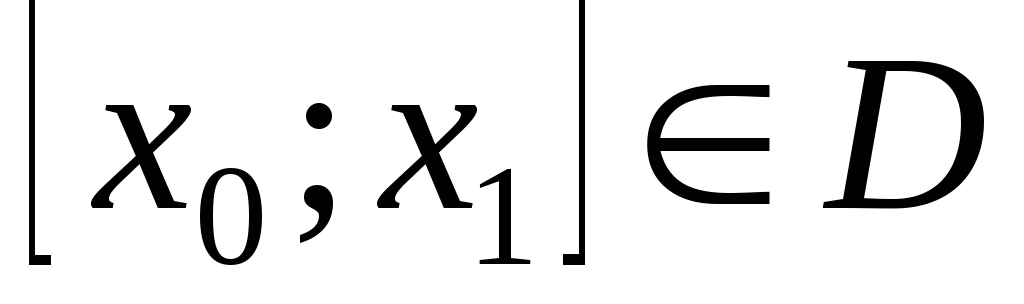, то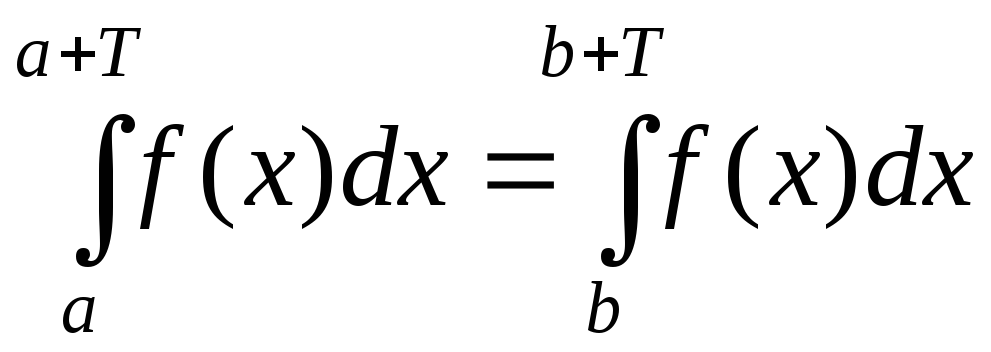при любыха иbпринадлежащих отрезку.

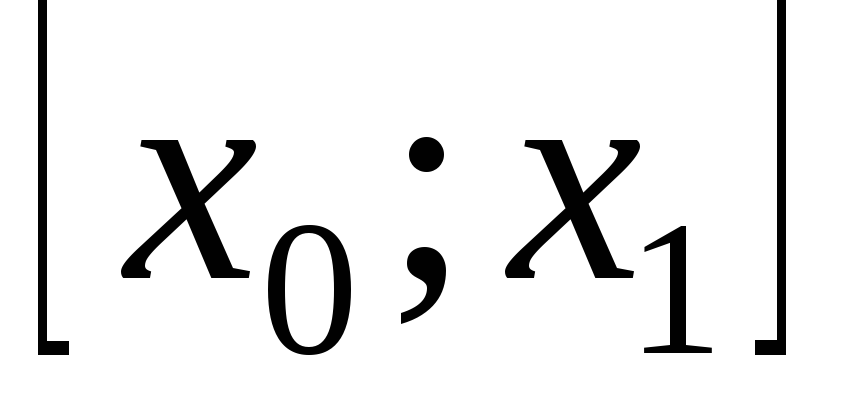Простейшими периодическими функциями являются тригонометрические функции и. Период этих функций равен.

Простейшим периодическим процессом является простое гармоническое колебание, описываемое функцией

(5.1.1)

, где А- амплитуда колебания,- круговая частота,- начальная фаза.

Функцию такого вида называют простой гармоникой. Период колебаний простой гармоники равен , т.е. одно полное колебание совершается за промежуток времени( ω показывает сколько колебаний совершает точка в течение 2π единиц времени).

Проведем преобразование функции для простого колебательного процесса: ,

где использованы обозначения .

Получили, что простое гармоническое колебание описывается периодическими функциямии.

В результате наложения конечного (или бесконечного) числа простых гармоник возникает сложное гармоническое колебание, также описываемое функциями вида и. Рассмотрим функцию

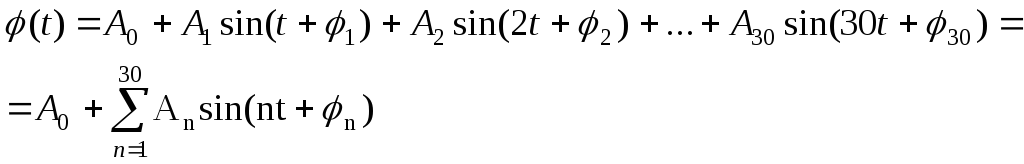
Эта функция состоит из суммы периодических функций, каждая из которых имеет период 2π/nи задает сложное гармоническое колебание с периодом2π.

Если какой-либо процесс имеет периодический характер, значит, описывающая его периодическая функция аналогична функции, представляющей собой сложное гармоническое колебание, состоящее из суммы простых гармоник.

Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник?

5.2 Тригонометрический ряд Фурье

Покажем, что практически любую периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники, с помощью, так называемого, тригонометрического ряда.

Определение. Тригонометрическим рядом называется функциональный ряд вида

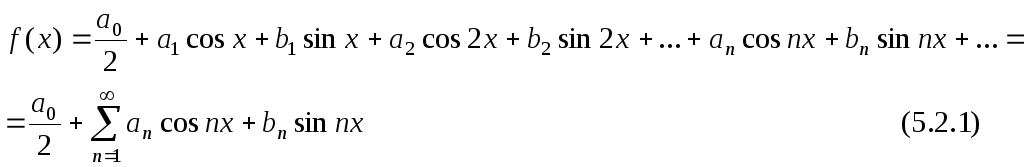
где действительные числа а₀,а_n,b_n называются коэффициентами ряда.

Свободный член ряда записан в виде для единообразия получающихся в дальнейшем формул.

Нужно решить два вопроса:

1. При каких условиях функция f(x) с периодом 2π может быть разложена в ряд (5.2.1)?

2. Как вычислить коэффициенты а₀,…а_n,b_n?

Начнем с решения второго вопроса. Пусть функция f(x) непрерывна на отрезкеи имеет периодТ=2π. Приведем формулы, которые понадобятся нам в дальнейшем.

1. 

При любом целом , так как функция четная.

2. 

При любом целом .

3. 

(mиnцелые числа)

4. 

5. 

При (mиnцелые числа) каждый из интегралов (III, IV, V) преобразуется в сумму интегралов (I) или ( II). Если же, то в формуле (IV) получаем:

_{Анологично доказывается равенство (V).}

Предположим теперь, что функция оказалась такой, что для неё нашлось разложение в сходящийся ряд Фурье, то есть

(5.2.2)

(Следует обратить внимание, что суммирование идёт по индексу n).

Если ряд сходится, то его сумму обозначим S(x).

Почленное интегрирование (законное в силу предположения о сходимости ряда) в пределах от додаёт

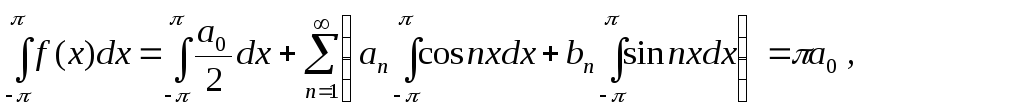
так как все слагаемые кроме первого равны нулю (соотношения I, II). Отсюда находим

_(5.2.3)

Умножая (5.2.2) на (m=1,2,…) и почленно интегрируя в пределах отдо, найдем коэффициентa_n.

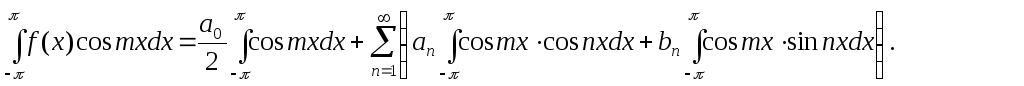_{В правой части равенства все слагаемые равны нулю, кроме одного m=n (соотношения IV, V), Отсюда получаем}

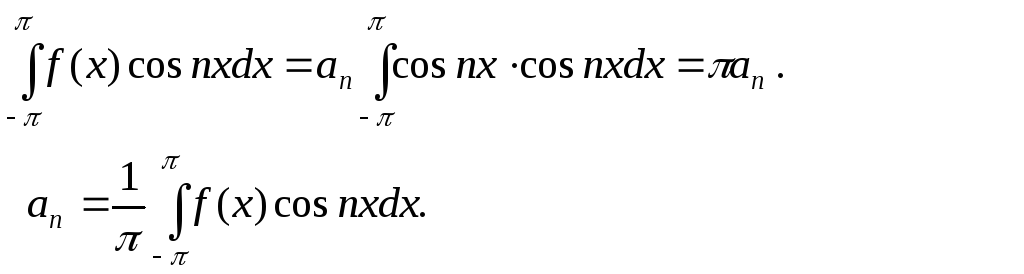_(5.2.4)

Умножая (5.2.2) на (m=1,2,…) и почленно интегрируя в пределах отдо,аналогичным образом находим коэффициентb_n

(5.2.5)

Значения - определяемые по формулам (5.2.3), (5.2.4), (5.2.5) называются коэффициентами Фурье, а тригонометрический ряд (5.2.2) – ряд Фурье для данной функцииf(x).

Итак, получили разложение функции f(x) в ряд Фурье

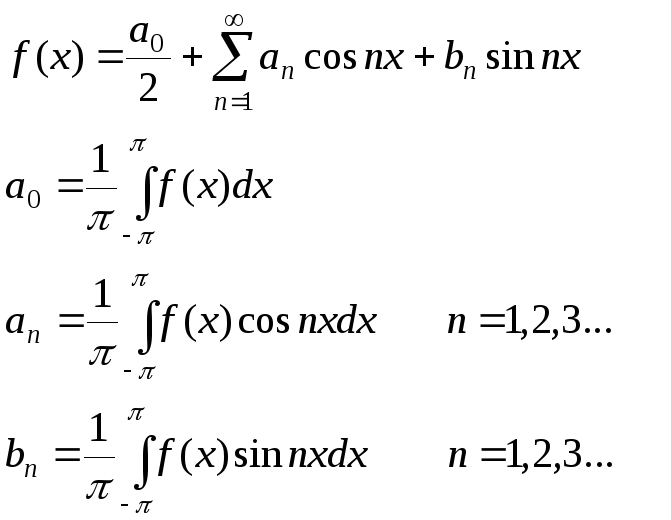
Вернемся к первому вопросу и выясним какими свойствами должна обладать функция f(x), чтобы построенный ряд Фурье был сходящимся, и сумма ряда равнялась бы именноf(x).

Определение. Функция f(x) называется кусочно-непрерывной, если она непрерывна или имеет конечное число точек разрыва I рода.

Определение. Функция f(x), заданная на отрезкеназываетсякусочно-монотонной, если отрезок можно разбить точкамина конечное число промежутков, в каждом из которых функция изменяется монотонно (возрастая или убывая).

Будем рассматривать функции f(x), имеющие периодТ=2π. Такие функции называются2π- периодическими.

Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.

Теорема Дирихле(примем без доказательства). Если2π-периодическая функцияf(x)на отрезке является кусочно-непрерывной и кусочно-монотонной, то соответствующий функции ряд Фурье сходится на этом отрезке и при этом:

1. В точках непрерывности функции сумма ряда совпадает с самой функцией S(x)=f(x);

2. В каждой точке х₀разрыва функцииf(x) сумма ряда равна,

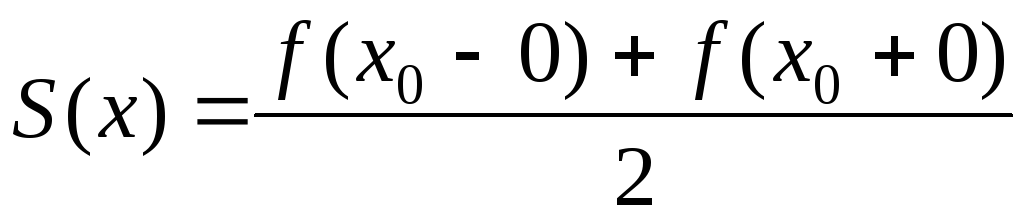т.е. среднему арифметическому пределов функции слева и справа от точки х₀;

3. В точках (на концах отрезка) сумма ряда Фурье равна,

т.е. среднему арифметическому предельных значений функции на концах отрезка, при стремлении аргумента к этим точкам изнутри промежутка.

Замечание: если функция f(x)с периодом 2π непрерывна и дифференцируема во всем промежутке и значения ее на концах промежутка равны, т.е., то ввиду периодичности эта функция непрерывна на всей числовой оси и при любомхсумма ее ряда Фурье совпадает сf(x).

Таким образом, если интегрируемая на отрезке функцияf(x)удовлетворяет условиям теоремы Дирихле, то на отрезкеимеет место равенство (разложение в ряд Фурье):

Коэффициенты вычисляются по формулам (5.2.3) - (5.2.5).

Условиям Дирихле удовлетворяет большинство функций, которые встречаются в математике и ее приложениях.

Ряды Фурье, как и степенные ряды, служат для приближенного вычисления значений функций. Если разложение функции f(x)в тригонометрический ряд имеет место, то всегда можно пользоваться приближенным равенством, заменяя данную функцию суммой нескольких гармоник, т.е. частичной суммой (2n+1) члена ряда Фурье.

Тригонометрические ряды широко используют в электротехнике, с их помощью решают многие задачи математической физики.

Пример .

Разложить в ряд Фурье функцию с периодом 2π, заданную на интервале (-π;π).

Решение. Найдем коэффициенты ряда Фурье:

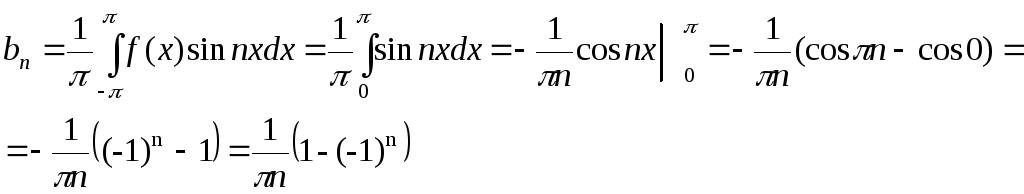
Получили разложение функции в ряд Фурье

В точках непрерывности сумма ряда Фурье равна значению функции f(x)=S(x), в точкех=0S(x)=1/2, в точкахх=π,2π,… S(x)=1/2.