6. Элементы операционного исчисления

Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.

6.1 Оригиналы и их изображение

Основными первоначальными понятиями операционного исчисления являются понятия функции – оригинала и функции-изображения.

Пусть f(t)– действительная функция действительного переменногоt(подtпонимается время или координата)

Определение. Функция f(t)называетсяоригиналом, если она удовлетворяет следующим условиям:

1. f (t) = 0 приt < 0

2. f (t)– кусочно-непрерывная приt 0

3. существуют такие числа M > 0иS₀ 0, что для всехtвыполняется неравенство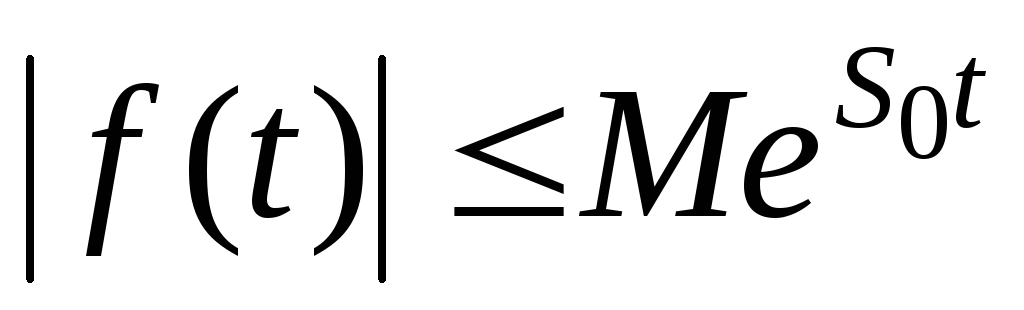, т. е. при возрастанииtфункцияf(t)может возрастать не быстрее некоторой показательной функции.

Число S₀ называется показателем ростаf(t).

Функция f(t)называется кусочно-непрерывной, если она непрерывна или имеет точки разрыва Iрода, причем на каждом конечном промежутке осиt лишь конечное число.

Условия (1-3) выполняются для большинства функций, описывающих различные физические процессы. Первое условие означает, что процесс начинается с некоторого времени; удобнее считать, что в момент t=0. Третьему условию удовлетворяют ограниченные функции (для нихS₀=0) , степенные (n > 0) и другие. Для функций вида, условие 3 не выполняется; не является оригиналом и функцияf(t)=-не выполняется 2-е условие.

Определение. Изображениеморигиналаf(t)называется функцияF(p)комплексного переменногор=,определяемая интегралом

.

Операцию перехода от оригинала f(t)к изображениюF(p) называютпреобразованием Лапласа. Соответствие между оригиналомf(t)и изображениемF(p)записывается в видеf(t)÷F(p). Принято оригиналы обозначать малыми буквами, а их изображения – соответствующими большими.

Пример 1.

Простейшим оригиналом является функция Хевисайда, определяемая следующим образом

Найдем изображение этой функции

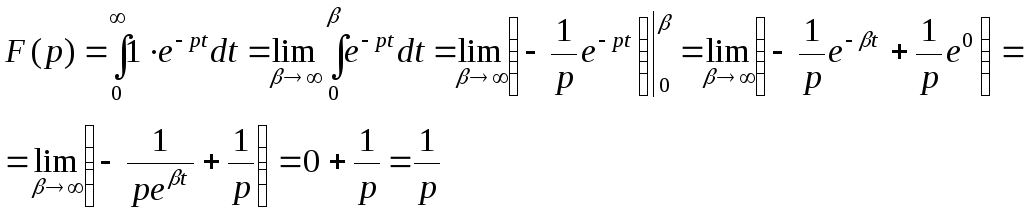
_, в символической записи.

Замечание: В дальнейшем функцию – оригинал будем коротко записывать в виде f(t), подразумевая, что.

Пример 2. Найти изображение функции ,а– любое число.

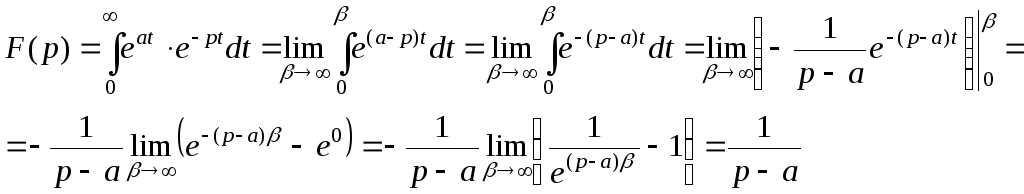
_{Получили .}

Пример 3. f(t) = t. Найти изображение. Пользуясь определением изображения составляем интеграл

_{(вычислить интеграл самостоятельно, применив формулу интегрирования по частям).}

6.2 Свойства преобразований Лапласа

Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа облегчают задачу нахождения изображений, а также задачу отыскания оригиналов по их изображениям.

Теорема(о единственности):

Если оригиналы f(t)иg(t)непрерывны и имеют одинаковое изображениеF(p), то эти функции совпадают.

Линейность: Линейной комбинации оригиналов соответствует такая же линейная комбинация изображения, т.е. если,с₁ ис₂ - постоянные числа, то

Пример: Найти изображения функций

1) f(t)=c -сonst

2) .Воспользуемся формулой

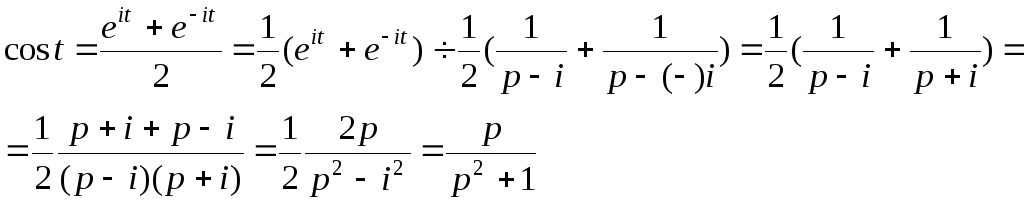
Для самостоятельной работы: найти изображения функций,используя формулы

; ;.

Подобие.

Если f(t)÷F(p),, то ,, т.е. умножение аргумента оригинала на положительное числоприводит к делению изображения и его аргумента на это число.

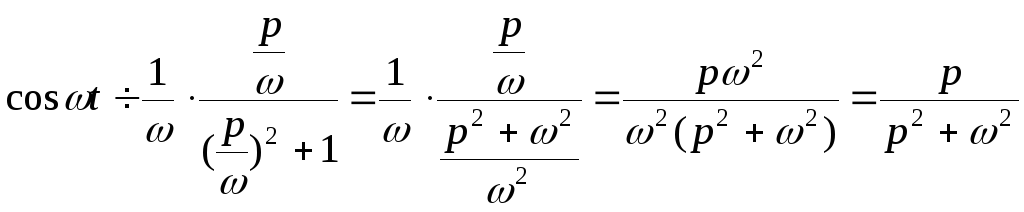
Смещение ( затухание ).

Если f(t)÷F(p),а =const, то, т.е. умножение оригинала на функциювлечет за собой смещение переменнойp.

Пример :

Запаздывание.

Если f(t) ÷ F(p),>0, то,т.е. запаздывание оригинала на положительную величинуприводит к умножению изображения оригинала без запаздывания на_.

Поясним термин «запаздывание».

Графики функций f(t)иf(t-λ) имеют одинаковый вид, но график функцииf(t-λ)сдвинут наединиц вправо.

Следовательно, функции f(t)иf(t-λ)описывают один и тот же процесс, но процесс описываемый функциейf(t-λ)начинается с опоздания на некоторое времяλ.

Функция называется обобщенной единичной функцией.

т.к. , то

Пример.

Дифференцирование оригинала.

Если f(t)÷F(p)и функцииявляются оригиналами, то

………………………………………………

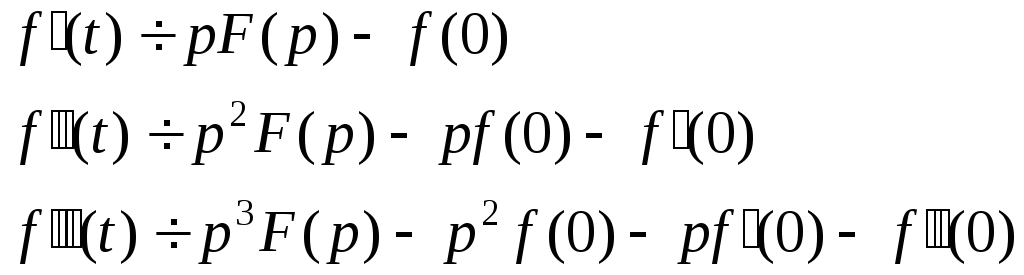
Дифференцирование изображения.

Если f(t)÷F(p), то

……………………………

Т.е.дифференцированию изображения соответствует умножение его оригинала на (-t).

Пример: т.к. , то имеем

Получили, что оригиналу t соответствует изображение.

Далее

Продолжая дифференцировать изображения далее, получим формулу

Интегрирование оригинала.

Если , то, т.е. интегрированию оригинала от 0 доt соответствует деление его изображения нар.

Интегрирование изображения.

Если и интегралсходится, то, т.е интегрированию изображения отрдосоответствует деление его оригинала наt.

Пример: Найти изображение функции

Т.к , то

Таблица оригиналов и изображений.

На основании вышеизложенных определений и свойств преобразования Лапласа составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).

Таблица оригиналов и изображений

№	Оригинал f(t)	Изображение	№	Оригинал f(t)	Изображение
1	1		11
2			12
3	t		13
4	(n-целое)		14
5			15
6			16
7			17
8			18
9			19
10

Примеры.

Используя таблицу изображений и свойство линейности найти изображения оригиналов:

1)

_{Найдем изображение каждого слагаемого, используя в таблице формулы 1, 4 и 15}

Используя свойство линейности , получаем:

2)

_{Данную функцию можно записать . Тогда по таблице (формула 2) получаем}

3) найти изображение оригинала

Используем формулу . Получаем

4)

Изображение гиперболического косинуса известно , применяя теорему смещения получаем.