1.8 Геометрические и физические приложения тройных интегралов

Объем тела.

Объем области выражается формулой

- в декартовых координатах,

- в цилиндрических координатах,

- в сферических координатах.

Масса тела.

Масса тела при заданной объемной плотности μ вычисляется с помощью тройного интеграла .

Статические моменты.

Моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz вычисляются по формулам

.

Центр тяжести тела.

Координаты центра тяжести тела V находятся по формулам

.

Моменты инерции тела

Моменты инерции тела относительно осей координат вычисляются по формулам

Моменты инерции тела относительно координатных плоскостей:

.

Момент инерции тела относительно начала координат.

.

В приведенных выше формулах μ(x;y;z) – функция плотности тела V.

Вопросы для самоконтроля.

1. Область интегрирования двойного интеграла. Изменение порядка интегрирования в двойном интеграле.

2. Вычисление двойных интегралов в декартовой системе координат..

3. Двойной интеграл в полярных координатах.

4. Геометрические приложения двойного интеграла.

5. Физические приложения двойного интеграла.

6. Вычисление тройного интеграла в прямоугольной системе координат.

7. Вычисление тройного интеграла в цилиндрической и сферической системе координат.

8. Вычисление объема цилиндрического тела с помощью тройного интеграла.

Литература: [5] стр. 160-210, [6] стр. 378-398, [7] стр. 445-459.

Примеры : [2] стр. 6-28, [3] стр. 4-95.

2. Криволинейные интегралы

2.1 Криволинейные интегралы второго рода. Основные понятия

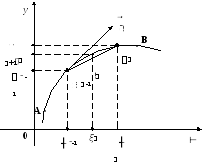Рассмотрим задачу: На материальную точку (x;y) действует переменная сила . Под действием этой силы точка перемещается по некоторой кривойАВ(от точкиАк точкеВ). Найти работу, которую производит сила на данном участке.

Решение.

Р

Рис. 22

азобьем кривуюАВнаn частей точкамиМ₀=А, М₁, …, М_i-1, M_i, …M_n=B. На каждой «элементарной дуге» возьмем произвольным образом точку (рис. 22). Заменим каждую дугу вектором , где . СилуF_iбудем считать постоянной на векторе перемещения и равной заданной силе в точкеС_i дуги , т.е. .

Работа есть скалярное произведение вектора силы и вектора перемещения.

- работа на i-ом участке. Работа на всей кривой будет равна сумме работ наi-ых участках, т.е. .

За точное значение работы Апримем предел полученной суммы

.

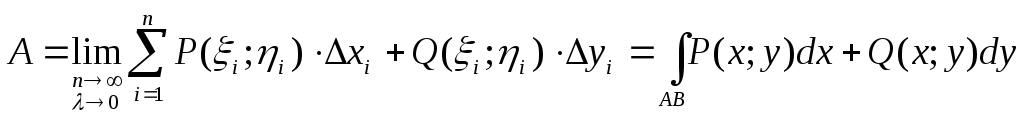Таким образом, работу можно вычислить, проинтегрировав вектор силы по дуге перемещения. Отвлекаясь от физического смысла интеграла, если при стремлении к нулю шага разбиения кривой АВинтегральные суммы имеют конечный предел, то этот предел называетсякриволинейным интегралом II рода (или интегралом по координатам) и обозначается

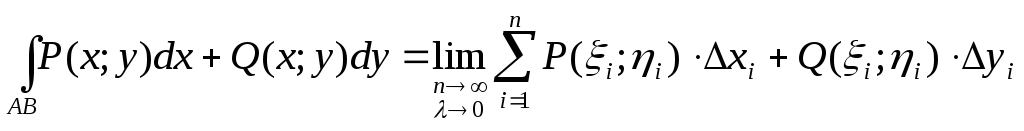
Аналогично определяется криволинейный интеграл по пространственной кривойL

Теорема. Если кривая АВ– кусочно-гладкая, а функцииP(x, y, z), Q(x, y, z)иR(x, y, z) – непрерывны на кривойАВ, то криволинейный интеграл II рода существует и не зависит от способа разбиения и выбора точки.

Свойства криволинейного интеграла второго рода.

1) Криволинейный интеграл при перемене направления пути интегрирования кривой меняет знак.

2) Если кривая АВ точкойСразбита на частиАС иСВ, то интеграл по всей кривой равен сумме интегралов по ее частям

3) Если кривая АВлежит в плоскости, перпендикулярной осиОх, то

Аналогичные соотношения справедливы при интегрировании для кривой, лежащей в плоскости, перпендикулярной оси Oyили осиOz ;

4) Криволинейный интеграл по замкнутой кривой Lне зависит от выбора начальной точки, а зависит только от направления обхода кривой (обозначается )

Направление обхода контураL задается дополнительно. ЕслиL– замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.