4.5 Ряды Тейлора и Маклорена

Формула Тейлора.

Наиболее простой функцией среди элементарных является многочлен. Он легко дифференцируется и интегрируется. Значения многочлена вычисляются так же значительно легче, чем других функций. В связи с этим встает вопрос, нельзя ли другие, более сложные функции заменить многочленами, не допуская при этом больших погрешностей. Этот вопрос положительно решен по отношению к некоторым функциям с помощью, так называемой формулы Тейлора.

Предположим, что функция f(x)имеет все производные до(n+1)-го порядка включительно, в некотором промежутке, содержащем точкух=а.

Найдем многочлен степени не вышеn, значение которого в точкех=аравняется значению функцииf(x)в этой точке, а значения его производных доn-го порядка в точкех=аравняются значениям соответствующих производных от функцииf(x)в этой точке, т.е. удовлетворяют условиям:

(4.5.1)

Будем искать этот многочлен в виде

(4.5.2)

Задача – определить коэффициенты .

Продифференцируем многочлен nраз

Подставим в формулу (4.5.2) и формулы (4.5.3) значение х=а, получим, используя условие (4.5.1)

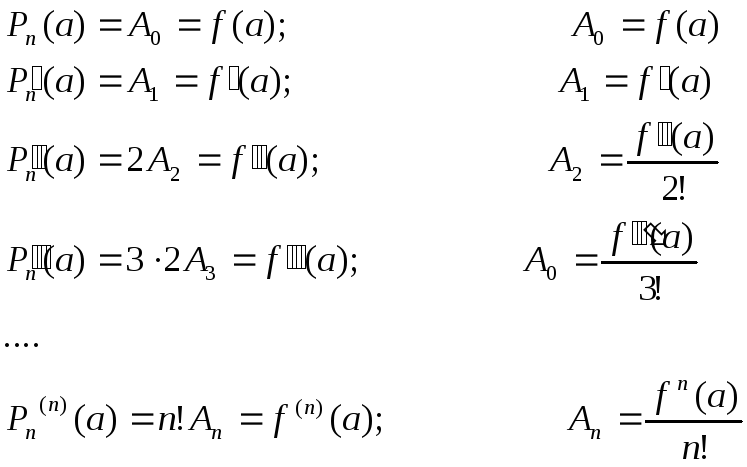
Получим искомый полином

Обозначим разность значений данной функции и построенного многочлена, т.е..

Получаем или

- ошибка, которую допускаем, заменяя данную функцию многочленом.называетсяостаточным членом. Для тех значенийх, при которых величинамала по сравнению с величиной, многочлен дает удовлетворительное “сближение” значенийи. Т.о., имеется возможность заменить функциюy=f(x) многочленомс соответствующей степенью точности, равной значению остаточного члена.

В полном курсе математического анализа доказывается, что остаточный член можно записать в форме Лагранжа:

В итоге получаем формулу Тейлора для функции

Если в формуле Тейлора положить a=0,то получаем частный случай формулы Тейлора –формулу Маклорена:

Обе формулы представляют собой степенные ряды, которые называются рядом Тейлора и рядом Маклорена.

Ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции в окрестности точки а,но отсюда ещё не следует, что он будет сходиться к данной функции. Ряд может оказаться расходящимся или сходящимся, но не к функции.

Теорема 1.Для того чтобы ряд Тейлора, функции, сходился к самой функции в точкех,необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при, т.е. чтобы

На практике пользуются ещё одной теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.

Теорема 2.Если модули всех производных функцииограничены в окрестности точких=аодним и тем же числом, то для любогох из этой окрестности ряд Тейлора функциисходится к функции, т.е. имеет место разложение

4.6 Разложение некоторых элементарных функций в ряд Маклорена

Для разложения функции в ряд Маклорена

нужно:

1. найти производные ,и т.д.;

2. вычислить значение производных в точке х=0;

3. написать ряд для заданной функции, найти его интервал сходимости;

4. найти интервал, в котором остаточный член ряда Маклорена при. Если такой интервал существует, то в нем функцияи сумма ряда Маклорена совпадают.

Выведем формулу разложения в ряд Маклорена для функции .

1)

2) при х=0

3)

4) Находим радиус сходимости

т.е. ряд сходится в интервале

5. Для всех имеемт.е. все производные в этом интервале ограничены одним и тем же числом, следовательно, по теореме 2

Т.о.

Пример: вычислить число е, взяв первые пять членов ряда и оценить ошибку

Пример: Вычислить с точностью 0,01.

Четвертое слагаемое 0,0083 меньше 0,01, поэтому для заданной точности достаточно сложить первые четыре члена ряда.

- число, которое показывает калькулятор.

Разложение в ряд Маклорена функции в точкех=0

1)

2) значение функции и производных в нуле

3)

4) интервал сходимости

5) любая производная функции по модулю не превосходит 1

следовательно

Имеет место разложение

6. Разложение для функции .

Воспользуемся свойством 3 степенных рядов.

Продифференцируем почленно ряд для , получим

Таблица разложения в ряд Маклорена некоторых элементарных функций.

1)

2)

3)

4)

(биноминальный ряд)

5)

6)

7)

8)

9)

10)

Примеры:

1) пользуясь таблицей получить разложение для функции . Воспользуемся биноминальным рядом

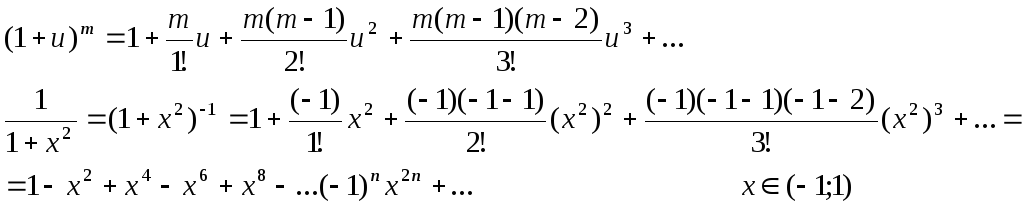
2) написать ряд Маклорена для функции

Воспользовавшись 4-м свойством степенных рядов, проинтегрируем ряд для функции , получим:

Можно показать, что ряд сходится и при и

При - лейбницевский ряд, сходится.

При - лейбницевский ряд , сходится .

Таким образом ряд для функции сходится для всех.