Практикум по ИО

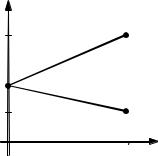
20. РАЦИОНАЛЬНАЯ СТОИМОСТЬ ОПЦИОНОВ

20.1. К р а т к и е т е о р е т и ч е с к и е с в е д е н и я и у к а з а н и я к в ы п о л н е н и ю з а д а н и й

Акция — это д о л е в о е обязательство: ее обладатель получает право долевого участия в управлении акционерной компанией, выпустившей эти акции (каждой акции соответствует определенное число голосов на ежегодном общем собрании акционеров — высшем органе управления компанией), в активах и прибылях (дивидендах) этой компании.

Рассмотрим ценообразование акций в рамках биномиальной модели

Кокса — Росса — Рубинштейна.

Предположим для простоты, что на рынке обращается о д н а акция, и ее стоимость в конце периода времени t составляет St.

Предположим также, что инвестор имеет возможность:

•размещать средства на банковском счете и брать с него в долг;

•покупать и продавать акции.

Будем считать, что проценты на банковский счет начисляются по схеме с л о ж н ы х п р о ц е н т о в с постоянной ставкой i(t) = i = const, так что в конце каждого года сумма на счете увеличивается в (1 + i) раз:

Bt = Bt–1(1+i).

Будем предполагать, что операционные издержки, связанные с пере% водом средств между активами, отсутствуют, а также что активы явля% ются безгранично делимыми, т. е. можно купить и продать любую часть акции, положить на счет и снять с него любую его часть.

Предположим, что в течение года времени стоимость акций может уве% личиться в u раз или увеличиться в d раз (уменьшиться в 1/d раз), причем d < 1 < 1 + i < u (рис. 20.1.1).

Рис. 20.1.1. Изменение цены акции за один год

Н а и д е а л ь н о м р ы н к е о т с у т с т в у ю т а р б и т р а ж н ы е в о з м о ж н о с т и, т. е. невозможно извлечь безрисковый доход, больший чем процент, начисляемый на банковский счет.

Предположение о том, что на рынке отсутствуют арбитражные воз5 можности, означает, что математическое ожидание цены акции на таком

181

рынке к концу года MS1 должно совпадать с суммой, которая оказалась бы на банковском счете к концу года, если бы сумма S0 была в начале года положена на банковский счет, т. е. с суммой S0(1 + i):

MS1 = S0(1 + i).

Истинные вероятности того, что в течение данного периода акция по% дорожает или подешевеет, нам неизвестны, но в предположении отсутст% вия арбитражных возможностей можно с помощью только что получен% ного условия вычислить так называемые вероятности, нейтральные к риску: пусть p — вероятность того, что в начале следующего периода це% на акции окажется равной S0u, тогда вероятность того, что цена акции бу% дет равна S0d, составит (1 – p); при этом

MS1 = S0up + S0d(1 – p).

Отсюда

S0up + S0d(1 – p) = S0(1 + i).

Разделим обе части этого равенства на S0:

up + d(1 – p) = 1 + i или (u – d)p + d = 1 + i,

Предположим теперь, что рассматриваемый промежуток времени [0; T] разбит на n периодов, в каждом из которых стоимость акции может уве% личиться в u или в d раз. Вероятность того, что стоимость акции увели% чится в u или в d раз, неизвестна, однако можно вновь воспользоваться принципом вероятности, нейтральной к риску.

При этом процентная ставка будет скорректирована. Рассчитаем про% центную ставку in, выплачиваемую за n%ю часть года в случае сложных процентов. За год сумма B0 увеличивается до B0(1 + i), с другой стороны, если n раз за этот год начислялся процент in по схеме сложных процентов, то к концу года сумма B0 должна превратиться в B0(1 + in)n. Таким обра% зом, заключаем, что

[индекс (n) здесь означает, что проведена коррекция годовой ставки с учетом того, что рассматриваемый отрезок времени [0; T] разбивается на n периодов].

182

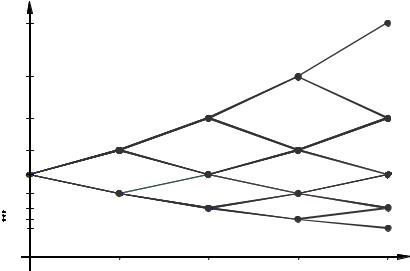
Теперь мы можем составить ряд распределения цены акции к концу чет% вертого периода: цена принимает значения

Банковский счет, акции и облигации называются основными финансо5 выми инструментами. На их базе могут быть построены более сложные финансовые инструменты — п р о и з в о д н ы е.

Наиболее распространенные типы производных финансовых инстру% ментов — форварды и опционы.

Опцион — это ценная бумага, представляющая собой договор, по кото% рому одна из сторон (продавец) продает опцион за определенную премию, а другая сторона (покупатель или владелец) при этом п о л у ч а е т п р а в о (но не обязанность) в течение срока, оговоренного в условиях оп% циона, либо купить определенный актив по фиксированной цене, опреде% ляемой в момент заключения договора и называемой терминальной стоимостью опциона (такой опцион называется опционом покупателя), либо продать актив по терминальной стоимости (такой опцион называет% ся опционом продавца).

По срокам исполнения опционы делятся на европейские и американ% ские. Американский опцион может быть предъявлен к исполнению в лю% бое время до истечения срока опциона, европейский опцион может быть использован только в день истечения его срока.

Рассмотрим ценообразование европейских опционов в рамках бино% миальной модели.

Рациональной считается такая стоимость финансового инструмента, которая исключает возможность арбитража без риска; иными словами, доходность безрискового финансового инструмента, имеющего рацио% нальную стоимость, должна совпадать с доходностью банковского счета.

Найдем рациональную стоимость T стандартного европейского оп% циона покупателя. Очевидно, рациональная стоимость опциона в момент его исполнения совпадает с прибылью, которую можно получить, испол% нив опцион. Данный опцион имеет смысл и с п о л н я т ь, т. е. пользовать% ся заложенным в нем правом покупки акции по цене X, лишь в том слу% чае, когда рыночная цена ST этой акции к моменту окончания срока дей% ствия опциона, т. е. к концу последнего периода, будет больше X . Если рыночная цена акции ST окажется больше X, держатель опциона, испол% нив его, получит доход (ST – X). Если же рыночная цена акции ST окажет% ся меньше X, держатель опциона просто не будет его исполнять и полу%

184

Справедлива

ТЕОРЕМА О ПАРИТЕТЕ ЕВРОПЕЙСКИХ ОПЦИОНОВ ПОКУПАТЕЛЯ И ПРОДАВЦА. Пусть одно5

временно заключаются два опционных контракта (опцион покупателя и опцион продавца) с одной и той же ценой исполнения X и одним и тем же сроком исполнения T на одну и ту же акцию, стоимость которой в началь5 ный момент равна S0, банковская (годовая) процентная ставка равна i. То5 гда рациональные стоимости этих опционов CT и PT связаны равенством

ПРИМЕР 20.1.3. Найти рациональную стоимость европейского опциона продавца с терминальной стоимостью X = 40 руб. и сроком исполнения 1 год, выписанного на акцию из условия примера 20.1.1.

Решение. По теореме о паритете опционов покупателя и продавца

откуда

P1 =2,24 −35 + 40 ≈3,60 , 1,11

т. е. рациональная стоимость такого опциона равна 3 руб. 60 коп.

Можно рациональную стоимость европейского опциона продавца найти и другим способом — по ряду распределения дохода от его исполнения

Находим математическое ожидание дохода от исполнения опциона:

MP1 =16,52 0,027 +11,33 0,158 +5,00 0,348 +0 0,467 =3,98.

и дисконтируем его на срок его действия:

(разница в две копейки образовалась из%за ошибок округления). Перейдем к рассмотрению ценообразования американских опционов. Оказывается, американский опцион покупателя может быть выгодно

исполнять только в последний момент срока его действия. Отсюда следует

ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ ЕВРОПЕЙСКИХ И АМЕРИКАНСКИХ ОПЦИОНОВ ПОКУПА2

ТЕЛЯ. Рациональная стоимость американского опциона покупателя сов5 падает с рациональной стоимостью аналогичного европейского опциона

мость может оказаться такой же, как у соответствующего европейского опциона (если досрочное исполнение окажется невыгодным) или выше (если будет выгоднее исполнить опцион досрочно).

186

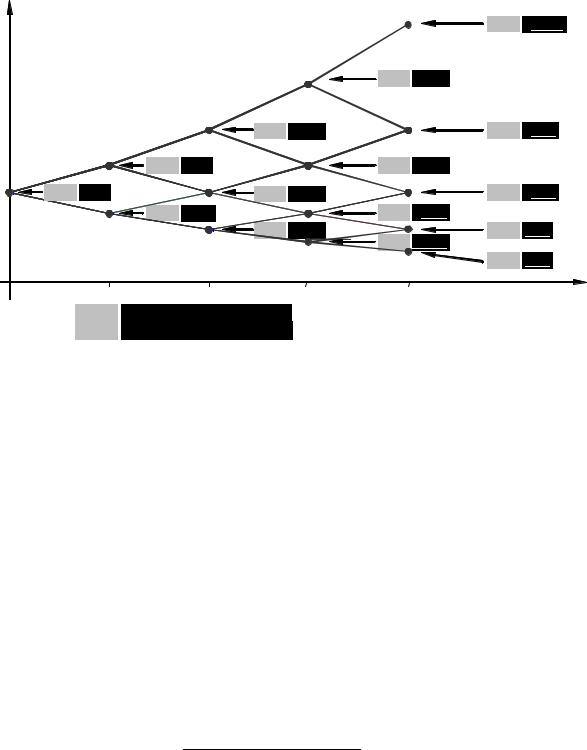
Рис. 20.1.3. Управление процессом владения американским опционом покупателя

Ожидаемый доход от исполнения опциона в будущем равен 12,18 0,595 +2,74 0,405 =8,36 .

Поскольку этот доход будут получен только через один период, дис% контируем его на четверть года — для сравнения с доходом от немедлен% ного исполнения опциона:

Аналогично вычислим ожидаемый доход от исполнения опциона во всех остальных вершинах дерева цен, двигаясь от конечного момента к начальному [см. рис. 20.1.3, на котором ожидаемые доходы от исполнения опциона в будущем изображены ч е р н ы м п о б е л о м у справа от (бе% ло%черных) доходов от немедленного исполнения опциона]. Выделим жирным и подчеркнем лучшее из двух: немедленное получение дохода или ожидание.

Окончательно получаем, что

C(амер.) = 3,48 0,595 +0,53 0,405 = . — 1 2,24 руб

1,024

действительно, оказалось невыгодно досрочное исполнение американского опциона покупателя, и его рациональная стоимость совпала с рациональ% ной стоимостью аналогичного европейского опциона покупателя.

В следующем примере разберем определение рациональной стоимости американского опциона продавца, который, как мы увидим, исполнять досрочно выгодно.

ПРИМЕР 20.1.5. Определить рациональную стоимость американского оп% циона продавца с терминальной стоимостью X = 40 руб. и сроком исполне% ния 1 год, выписанного на акцию из условия примера 20.1.1.

188

просто означает, что такой инструмент рациональному инвестору в прин% ципе покупать не следует.

Найти рациональные стоимости опционов европейских и американских покупателя и продавца с терминальной стоимостью X руб. и сроком испол% нения 1 год, выписанных на акцию, текущая цена которой равна S0 руб., если известно, что годовая безрисковая процентная ставка составляет i = 10%, а год разбивается на четыре периода, в каждом из которых акция может возрасти в цене или упасть в цене в u раз (параметры X, S0 и u