Практикум по ИО
.pdf
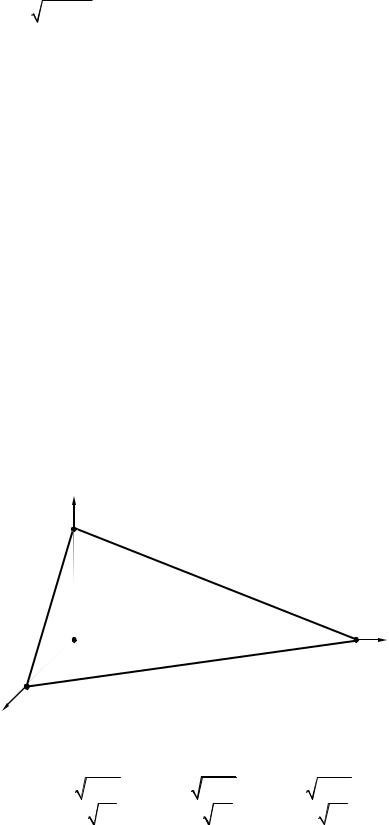
Из рис. 14.1.1 видно, что снижение полезности, вызванное уменьшением количества одного товара, можно, вообще говоря, к о м п е н с и р о в а т ь увеличением количества другого товара. Рассмотрим некоторый набор товаров
x10
x20
= x0
x0 i
x0j
xn0
и предположим, что количество i%го товара изменилось на величину dxi, количество j%го товара изменилось на dxj, а все остальные товары оста% лись в тех же количествах, что и раньше; новый набор товаров
|
|
|
|
x0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
+ dxi |
|
|
x |
xi |
|
||||
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+ dxj |
|
||
|
|
xj |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
x2
u(x1, x2) = u0 = const
grad u(x1, x2 ) |
x1
0
Рис. 14.1.1. Поверхность безразличия и градиент функции полезности
141
Чтобы старый и новый наборы товаров оказались на одной поверхности безразличия, необходимо выполнение условия (14.1.2). Учтем, что dxk = 0 при k ≠i, k ≠ j , тогда получим, что
|
|
|
∂u |
dxi + |
∂u |
dxj =0 , |
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
∂xi |
|
|
∂xj |
|
|
|
|
|
|||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxj |
=− |
∂u/∂xi |
. |
|
|
|||||||
|
|
|
|
dxi |
∂u/∂xj |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
= |
lim |
|
xj |
=− |
dxj |
= |
∂u/∂xi |
. |
|||||||
ri |
|
|
|
|
|
|||||||||||
− xi |
dxi |
∂u/∂xj |
||||||||||||||
|
|
u(x)=const |
|
|
|
|
|
|||||||||
|
|
xi →0, |
|
|
|
|
|
|
|
|
|
|
||||
называется предельной нормой замены i%го товара j%м; она показывает, на сколько е д и н и ц должно увеличиться количество j%го товара, чтобы к о м п е н с и р о в а т ь потерю единицы i%го товара (т. е. чтобы полез% ность набора товаров не изменилась).
Часто бывает удобно иметь дело не с абсолютными величинами, а с о т н о с и т е л ь н ы м и. Эластичность замены i%го товара j%м ( eij ) пока% зывает, на сколько п р о ц е н т о в должно увеличиться количество j%го товара, чтобы компенсировать уменьшение количества i%го товара на 1%:
j |
= lim |
|
xj |
/ xj |
=− |
xi |
lim |
xj |
= |
xi |
j |
= |
xi |
∂u/∂xi |
. |
ei |
|
|
|
|
|
|
ri |
|
|
||||||
− |
xi / xi |
|
xi |
xj |
xj |
∂u/∂xj |
|||||||||
|
xi →0, |
|
|
xi →0, |
|
|
|
|
|||||||
|
u(x)=const |
|
xj u(x)=const |
|
|
|
|
||||||||
Теперь сформулируем математически задачу потребителя: требует5 ся из бюджетного множества выбрать набор товаров, обладающий максимальной полезностью:
u(x) →max, x B.
Запишем эту задачу подробнее [с учетом (14.1.1)]:
|
u(x1, x2 |
,…, xn ) →max, |
|
||||||||
p x |
+ p x |
+ |
+ p x |
n |
I, |
(14.1.3) |
|||||
|
1 1 |
|
2 |
2 |
|
|
n |
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
x |
0, |
0, |
…, |
n |
|
0. |
|
||||
|
1 |
|
2 |
|
|
|
|||||
ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ЗАДАЧИ ПОТРЕБИТЕЛЯ. Решение
x1
x2
xn
142
задачи потребителя (14.1.3) существует и лежит на границе бюджет5 ного множества:
p x + p x + |
+ p x |
= I . |
(14.1.4) |
1 1 2 2 |
n n |
|
|
ТЕОРЕМА ЕДИНСТВЕННОСТИ РЕШЕНИЯ ЗАДАЧИ ПОТРЕБИТЕЛЯ. Если функция по5
лезности является строго выпуклой вверх, то решение задачи потре5 бителя (14.1.3) является единственным.
Сучетом (14.1.4) задачу потребителя можно переписать в виде к л а с %
си ч е с к о й з а д а ч и н а у с л о в н ы й э к с т р е м у м:
u(x1, x2,…, xn ) →max, (14.1.5) p1x1 +p2x2 + +pnxn = I.
Задачу (14.1.5) можно решить с помощью м е т о д а м н о ж и т е л е й Л а г р а н ж а: функция Лагранжа
L(x1, x2,…, xn , λ) = u(x1, x2,…, xn ) + λ(I −p1x1 −p2x2 − −pnxn ) ,
условный максимум в задаче (14.1.5) совпадает с безусловным максиму% мом функции Лагранжа, который удовлетворяет следующим условиям:
|
∂L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0, |
||
|
|
|
||
∂xi |
|
|
||
|
|
|
|
|
∂L |
=0 |
|||
|
|
|
||
|
|
|||
|
∂λ |
|
|
|
|
|
|
||
i |
= |
1, 2, |
… |
, n, |
|
|
|
|
||
|
|
∂u |
|
|
|
|||||
|
|
|
|
|
|
|
|
−λpi =0, |
i =1, 2,…, n, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
∂xi |
|
|||
|
|
|
|
|
|
|
|
− −pnxn =0 |
|
|
|
|
|
|
|
|
I −p1x1 −p2x2 |
|
|||
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= λpi , |
i =1, 2,…, n, |
|
|||
|
|
∂xi |
|
|||||||
|
|
|
(14.1.6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p1x1 +p2x2 + +pnxn = I. |
|
|||||||
Условия (14.1.6), определяющие оптимальное решение задачи потреби% теля, означают, в частности, что при ценах p1, p2, …, pn потребитель, обла% дающий богатством I, выбирает набор товаров, который соответствует полному использованию богатства I, причем вектор предельных полезно% стей товаров пропорционален вектору цен:
|
∂u |
: |
∂u |
:…: |
∂u |
= p1 : p2 :…: pn . |
|||||
|
|
|
|
||||||||
|
∂x |
∂x |
|
∂x |
n |
|
|||||
1 |
|
2 |
|
|
|
|
|||||
Отсюда следует, что в |
о п т и м а л ь н о й |
т о ч к е предельная норма |
|||||||||
замены i%го товара j%м равна отношению цен i%го и j%го товаров: |
|||||||||||
|
|
|
rij = |
∂u/∂xi = |
pi |
. |
(14.1.7) |
||||
|
|
|
|
||||||||
|
|
|
|
|
∂u/∂xj pj |
|
|||||
Равенство (14.1.7) можно содержательно интерпретировать в виде вто, рого закона Госсена: взаимозаменяемыми являются такие количества то% варов, которые имеют одинаковую стоимость.
143
Можно сделать еще один вывод из условий (14.1.6): у всех товаров в о п т и м а л ь н о й т о ч к е отношения предельных полезностей к ценам совпадают и равны λ :
∂u/∂x1 = ∂u/∂x2 = = ∂u/∂xn = λ . p1 p2 pn
Это дает ответ на вопрос об экономическом смысле множителя Ла,
гранжа λ : множитель |
Лагранжа равен п р е д е л ь н о й п о л е з н о % |
с т и о д н о й д е н е ж |
н о й е д и н и ц ы (поскольку в оптимальной точ% |
ке часть предельной полезности каждого товара, приходящаяся на еди% ницу его цены, равна λ ).
Если из условий (14.1.6) выразить x как функцию от цен и богатства, то получим функцию спроса данного потребителя: x = x (p1, p2,…, pn , I) .
Рассмотрим, как изменится спрос потребителя, если изменится цена одного из товаров (например, j%го).
Предположим вначале, что при изменении цены j%го товара на величи%
ну pj (при |
неизменных ценах остальных товаров) происходит к о м % |
п е н с а ц и я |
б о г а т с т в а на такую величину I , чтобы новая точка |
оптимального спроса осталась на той же поверхности безразличия, что и старая [иными словами, чтобы полезность набора товаров
|
|
x′= x (p1, p2,…, pj + pj ,…, pn , I + I), |
|
|
|
||||||
оптимального при векторе цен p =(p1 |
p2 |
pj + |
pj |
|
pn ) и богат% |
||||||
стве M + M , была бы равна полезности набора товаров |
|
|
|
||||||||
|
|
x = x (p1, p2,…, pj ,…, pn , I) , |
|
|
|
|
|||||
оптимального при векторе цен p =(p1 |
p2 |
pj |
pn ) |
и богатстве I |
|||||||
(рис. 14.1.2)]. |
|
|
|
|
|
|
|
|
|
||
Если теперь устремить pj |
к нулю и рассмотреть предел |
|
|
|
|||||||
|
|
|
xi |
|
|
xi′−xi |
|
|
|
|
|
|
|
lim |
= |
lim |
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
pj →0, |
pj |
pj →0, |
pj |
|
|
|
|
||
|
|
u(x′)=u(x ) |
|
u(x′)=u(x ) |
|
|
|
|
|
|
|
= |
|
xi (p1, p2,…, pj + pj ,…, pn , I + I)−xi (p1, p2,…, pj |
,…, pn , I) |
||||||||
lim |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
pj |
|
|
|
|
|
|||
|
pj →0, |
|
|
|
|
|
|
|
|
||
|
u(x′)=u(x ) |
|
|
|
|
|
|
|
|
|
|
то мы получим изменение спроса на i%й товар при изменении цены j%го товара на единицу и сопутствующем компенсирующем изменении богат%
ства; это изменение обозначается
∂xi
∂pj комп.
= lim |
xi . |
pj →0, |
pj |
u(x′)=u(x ) |
|
144

∂xi |
|
∂xi |
− |
∂xi |
|
|
i =1, 2,…, n, |
j =1, 2,…, n . |
|
||
|
|
|
|
|
|
j |
, |
(14.1.9) |
|||
∂p |
|
= |
∂p |
|
∂I |
x |
|||||
j |
|
|
|
|
|
|
|
|
|||
|
|
j комп. |
|
|
|
|
|
|
|
||
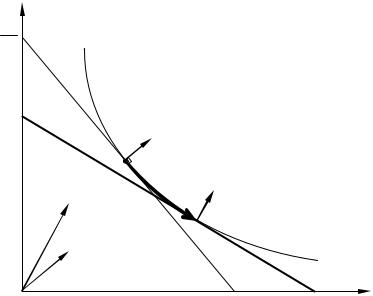
Уравнение (14.1.9), полученное в 1915 г. Е. Е. Слуцким, играет важней% шую роль в теории потребительского спроса. Вычитаемое в этом уравне% нии отражает э ф ф е к т д о х о д а, связанный с изменением потреби% тельской ценности единицы богатства. Фактически потребитель не оста% ется на той же поверхности безразличия, что и раньше, а переходит на другую поверхность безразличия, соответствующую другим количествам товаров, которые он может позволить себе приобрести при изменении це% ны j%го товара и неизменном богатстве и ценах остальных товаров. Эф% фект дохода и эффект замещения иллюстрируется рис. 14.1.3.
|
|
x2 |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
p2 |
u(x) = const |
|
|
|
|||
|
|
|
|
|
|
|||
I + |
I |
|
|
|
|
|
|
|
p2 + |
p2 |
x grad u(x ) p |
эффект |
|||||
I |
|
|
|
|
|
замещения |
||
p2 + |
p2 |
grad u(x′) p′ |
||||||
|
|
|
||||||
|
|
p′ |
x′ |
|
|
|
||
|
|
|
x′′ |
|
|
|
||
|
|
p |
эффект дохода |
|
|
x1 |
||
|
|
|
|
|
||||
|
0 |
|
I |
|
|
I + I |
|
|
|
|
|
|
p1 |
|
p1 |
||
Рис. 14.1.3. Эффект дохода и эффект замещения
Можно показать, что
∂x
i <0 , (14.1.10)
∂pi комп.
т. е. при увеличении цены (i%го) товара спрос на него падает даже в том случае, если увеличение цены сопровождается компенсирующим изме% нением богатства.
Товар с номером i называется ценным, если при увеличении богатства спрос на него растет, т. е. если
∂x
i >0 , (14.1.11)
∂I
и малоценным, если при увеличении богатства спрос на этот товар сни% жается:
146
• т о в а р ы Г и ф ф и н а, в качестве примера такого товара традиционно приводят картофель в Ирландии XIX в.: в то время большая часть потре% бительских расходов населения тратилась на приобретение картофеля, но по мере увеличения богатства потребители предпочитали покупать больше мяса и меньше картофеля; при увеличении цены картофеля ре% альный доход потребителя уменьшался настолько, что он уже не могли покупать столько же мяса, как и прежде, и потому был вынужден увели% чивать потребление картофеля.
Два товара с номерами i и j называются взаимозаменяемыми, если увеличение цены j%го товара при сопутствующем компенсирующем из% менении богатства приводит к увеличению спроса на i%й товар:
|
∂xi |
>0 ; |
|
|
|
|
|
|
∂p |
|
|
|
|
|
|
|
j комп. |
|
|
товары называются взаимодополняющими, если увеличение цены j%го товара при сопутствующем компенсирующем изменении богатства ведет к уменьшению спроса на i%й товар:
|
∂xi |
>0 . |
|
|
|
|
|
|
∂p |
|
|
|
|
|
|
|
j комп. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а 14.1.1 |
|
|
|
|
|
||||||||
|
|
Влияние изменения |
ценные товары: |
малоценные товары: |
||||||||
|
|
дохода |
|
|
|
|
|
|
|
|
|
|
Влияние |
|
|
|
|
|
|
|
|
|
∂xi >0 |
∂xi <0 |
|
|
|
|
|
|
|
|
|
|
∂I |
∂I |
||
изменения цены товара |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
нормальные товары: |
∂xi |
<0 |
|
|
|
|
|
пример: мясо |
пример: маргарин |
|||
|
|
∂pi |
|
|
|
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|
|
пример: картофель |
товары Гиффина: |
>0 |
|
|
|
|
|
|
|
— |
в середине XIX в. |
||
|
|
∂pi |
|
|
|
|
|
|
|
|
|
в Ирландии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Эти определения корректны, поскольку можно показать, что матрица |
||||||||||||
|
|
|
|
|
|
|
∂x |
|
|
n n |
|
|
|
|
|
|
|
|
= |
i |
|
|
× |
|
|
|
|
D = d |
ij |
|
|
|
|
|
||||
|
|
|
|
|
|
∂p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
комп. |
|
|
|
|
является с и м м е т р и ч н о й, |
т. е. |
|
|
|
|
|
|
|||||
|
∂xi |
|
∂xj |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
, |
i =1, 2,…, n, j =1, 2,…, n . |
|||||
|
|
|||||||||||
|
|
|
∂pi |
|
|
|
|
|
|
|
|
|
∂pj |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
комп. |
|
|
|
|
|
|
||
|
комп. |
|
|
|
|
|
|
|
|
|
|
|
Примерами пар взаимозаменяемых товаров являются яблоки и груши, чай и кофе, сыр и колбаса и т. п.; примерами пар взаимодополняющих то% варов являются компьютеры и компьютерные принтеры, автомобили и бензин, брюки и ремни и т. д.
148