Практикум по ИО

13. БИМАТРИЧНАЯ ИГРА

13.1. К р а т к и е т е о р е т и ч е с к и е с в е д е н и я и у к а з а н и я к в ы п о л н е н и ю з а д а н и й

Не все конфликтные ситуации можно представить как игры с нулевой суммой, потому что интересы участников таких конфликтов не всегда противоположны.

Обобщением игр с нулевой суммой на случай н е п р о т и в о п о л о ж % н ы х и н т е р е с о в участников являются игры с ненулевой суммой.

Первый игрок может выбрать одну из m своих стратегий, обозначен% ных номерами i = 1, 2, …, m, а второй игрок — одну из n своих стратегий, обозначенных номерами j = 1, 2, …, n, Если первый игрок выбрал свою i%ю стратегию, а второй игрок — свою j%ю стратегию, то в результате такого совместного выбора первый игрок получает выигрыш aij , а второй игрок

— выигрыш bij . При этом совершенно не обязательно, чтобы bij = −aij , как

в матричной игре.

Таким образом, игра с ненулевой суммой определяется двумя матри% цами

Конечная игра с ненулевой суммой полностью определяется этими двумя матрицами, поэтому называется биматричной.

Биматричная игра, как и матричная, происходит партиями. Цель каж% дого игрока — выиграть как можно большую сумму в результате большо% го числа партий. Аналогично матричным играм, вводятся понятия чистых и смешанных стратегий игроков в биматричной игре.

Если матричные игры являются играми со строгим соперничеством, по% скольку выигрыш одного игрока в точности равен проигрышу другого, то в биматричных играх интересы игроков могут быть в большей или мень% шей степени близки.

В зависимости от того, запрещено или разрешено сотрудничество иг% роков, различают некооперативные и кооперативные игры.

Анализ биматричной игры в некооперативном варианте сводится к поиску максиминных стратегий игроков, т. е. стратегий, которые обес% печивают игрокам получение максимально возможного гарантированного выигрыша вне зависимости от действий противника.

Множество всевозможных пар смешанных стратегий игроков обозначим

S ={(p, q): p S1, q S2},

где

131

Если два игрока выбрали с м е ш а н н ы е с т р а т е г и и

соответственно, то математические ожидания выигрышей игроков равны соответственно

Максиминные стратегии первого и второго игроков обеспечивают им гарантированные выигрыши

соответственно вне зависимости от поведения противника.

В некооперативном случае игрокам имеет смысл придерживаться сво% их осторожных стратегий (т. е. максиминных).

Обсудим теперь подходы к анализу биматричной игры в кооператив, ном варианте.

можные варианты пар выигрышей представляют собой выпуклую обо% лочку точек плоскости с координатами (aij , bij ), i =1, 2,…, m, j =1, 2,…, n ; эти точки соответствуют выигрышам игроков в случае выбора им своих ч и с т ы х с т р а т е г и й.

это означает, что при переходе от первой точки ко второй выигрыш каж% дого из игроков не уменьшится, и при этом хотя бы у одного из игроков выигрыш увеличится.

132

Максиминные стратегии игроков определяются из условий

Таким образом, максиминные стратегии первого и второго игрока рав% ны соответственно

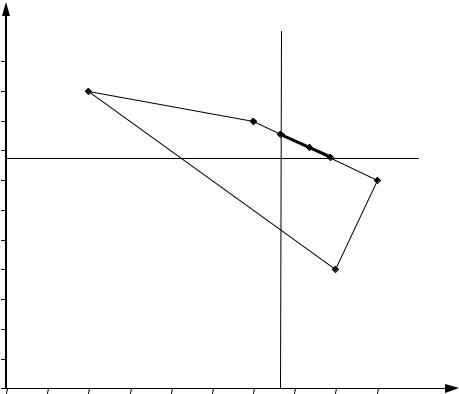
Множество всех возможных пар выигрышей игроков представлено че% тырехугольником ABCD на рис. 13.1.1. Очевидно, множество Парето соот% ветствует отрезку BC, а переговорное множество — отрезку EF.

Рис. 13.1.1. Множество ожидаемых выигрышей, множество Парето и переговорное множество

Прямая, проходящая через точки B(6; 9) и C(9; 7), задается уравнением M2 =13 −2M1 /3 , поэтому функция Нэша

134

14. МОДЕЛЬ ПОВЕДЕНИЯ ПОТРЕБИТЕЛЯ

14.1. К р а т к и е т е о р е т и ч е с к и е с в е д е н и я и у к а з а н и я к в ы п о л н е н и ю з а д а н и й

Рассмотрим рынок, на котором продаются товары n видов. Пусть p1, p2, …, pn — цены этих товаров, вектор

p =(p1 p2 pn )

естественно назвать вектором цен.

Пусть некоторый потребитель обладает богатством M ден. ед., и xi — это количество единиц i%го товара, которые данный потребитель приоб% ретает на рынке (i = 1, 2, …, n). Вектор

x1

x = x2 ,xn

координаты которого неотрицательны и соответствуют приобретаемым количествам товаров каждого вида, называется набором товаров, а мно% жество всех наборов товаров

называется пространством товаров (поскольку на наборы товаров не налагается ограничений целочисленности, здесь предполагается, что можно приобрести произвольное — целое или дробное — количество лю% бого товара, т. е. что все товары являются б е з г р а н и ч н о д е л и м ы % м и).

Стоимость набора товаров x равна, очевидно,

px = p1x1 + p2x2 + + pnxn .

Бюджетное множество B — это множество наборов товаров x C , ко% торые может себе позволить приобрести при данных ценах p1, p2, …, pn по% требитель, обладающий богатством I (при этом предполагается, что тра% тить в с е деньги необязательно).

С алгебраической точки зрения бюджетное множество описывается системой линейных неравенств

ТЕОРЕМА О БЮДЖЕТНОМ МНОЖЕСТВЕ. Бюджетное множество является выпуклым, ограниченным и замкнутым.

Потребитель р а з л и ч а е т наборы товаров: один набор товаров он может считать для себя б о л е е п р е д п о ч т и т е л ь н ы м, чем другой, два каких%то других набора товаров он может считать р а в н о ц е н н ы % м и. Запись x y означает, что потребитель считает набор товаров x н е

ху ж е набора товаров y.

Вкачестве первой аксиомы потребителя примем, что относительно любых двух наборов товаров x, y C потребитель может однозначно ска%

р а в н о ц е н н о с т ь наборов товаров x и y с точки зрения данного потре% бителя: x не хуже y, а y не хуже x;

и « »:

• отношения слабого предпочтения и равноценности являются рефлек5 сивными (т. е. для любого набора товаров x C верно, что x x и x x );

• отношения слабого предпочтения, равноценности и сильного предпоч% тения являются транзитивными (т. е. для любых наборов товаров x, y, z C из того, что x y , а y z , следует, что x z ; из того, что x y , а y z , следует, что x z ; из того, что x y , а y z , следует, что x z );

•отношение равноценности является симметричным (т. е. из того, что x y , следует, что y x ).

Третья аксиома потребителя говорит о том, что каждый товар являет% ся для потребителя желательным, т. е. если x y , то x y , а если x > y , то x y .

Рациональное поведение потребителя состоит в выборе наиболее пред% почтительного, с его точки зрения, набора товаров из бюджетного множе% ства. При постановке и решении задачи определения рационального по% ведения потребителя удобнее оценивать привлекательность различных наборов товаров не с помощью отношений предпочтения и равноценно% сти, а с помощью функции полезности, которая ставит в соответствие каждому набору товаров x C некоторое число u(x) — п о л е з н о с т ь данного набора товаров — и удовлетворяет двум условиям:

138

u(x) = u(x1, x2,…, xn ) = x1α1 x2α2 xnαn ,

где α1, α2,…, αn >0, α1 +α2 + +αn <1;

• логарифмическая:

n

u(x) = u(x1, x2,…, xn ) = ∑ai logd xi ,

i=1

где a1, a2,…, an >0 , d >1;

• квадратичная:

где матрица B =(bij ) должна быть отрицательно определенной;

• пропорциональная:

где k1, k2,…, kn >0 и др.

Множество р а в н о ц е н н ы х с точки зрения данного потребителя на% боров товаров называется поверхностью безразличия. Если u(x) — функ% ция полезности данного потребителя, то поверхность безразличия — это множество наборов товаров, обладающих одинаковой полезностью:

{x C | u(x) = u0 = const}.

С геометрической точки зрения поверхность безразличия в простран% стве n товаров представляет собой гиперповерхность (n – 1)%го порядка.

В дифференциальной форме условие u(x) = u0 = const записывается так:

Г р а д и е н т функции полезности равен вектору предельных полезно% стей:

∂∂u

∂x1

= ∂u

grad u x .

∂∂u2

xn

Условие (14.1.2) означает, что градиент функции полезности перпенди% кулярен касательной к поверхности безразличия (рис. 14.1.1).

140