Практикум по ИО

указано, какую долю рынка получит наше предприятие, если оно будет действовать согласно каждой из возможных трех стратегий, а основной конкурент — согласно каждой из своих возможных трех стратегий.

Решение. Данная игра имеет седловую точку. Действительно, нижняя цена игры

α = max min aij =max{0,1, 0,3, 0,1} =0,3

i=1,2,3 j=1,2,3

(соответствует второй стратегии первого игрока), а верхняя цена игры

β = min max aij =min{0,5, 0,3, 0,4} =0,3

j=1,2,3 i=1,2,3

(соответствует второй стратегии второго), поэтому игроки, действуя каж% дый по своей второй стратегии, могут гарантировать себе: первый — вы% игрыш не менее ν = α =β =0,3 =30% рынка, а второй — что первый игрок выиграет не более ν =30% рынка. Таким образом, оптимальная чистая стратегия первого игрока — вторая, второго игрока — вторая, а цена игры равна ν =0,3 .

Смешанной стратегией первого игрока называется вектор

m

где все pi 0 ( i =1, 2,…, m ), а ∑pi =1. При этом pi — вероятность, с кото%

i=1

рой первый игрок выбирает свою i%ю стратегию. Аналогично определяет% ся смешанная стратегия

q1 q = q2qn

второго игрока. Чистая стратегия также подпадает под определение сме% шанной — если все вероятности равны нулю, кроме одной, равной единице.

Если игроки играют своими смешанными стратегиями

соответственно, то математическое ожидание выигрыша первого игрока равно

m n

M(p,q) = ∑∑piqjaij

i=1 j=1

(и равно математическому ожиданию проигрыша второго игрока).

121

называются оптимальными смешанными стратегиями соответственно первого и второго игрока, если

M(p,q ) M(p ,q ) M(p ,q) .

Если у обоих игроков есть оптимальные смешанные стратегии, то пара (p ,q ) называется решением игры (или седловой точкой в смешанных стратегиях), а число ν = M(p ,q ) — ценой игры.

ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ ИГР. В любой матричной игре у игроков есть оптимальные смешанные стратегии.

Интересно отметить, что игры с полной информацией (когда игроки при каждом своем ходе знают результаты всех предыдущих ходов) имеют седловую точку, а значит, и решение в чистых стратегиях. В частности, играми с полной информацией являются шахматы, шашки, «крестики% нолики» и др. Оптимальные стратегии при игре в шахматы пока не най% дены ввиду слишком большого числа стратегий, однако прогресс в облас% ти компьютерной техники позволяет прогнозировать решение этой зада% чи в обозримом будущем.

ПРИМЕР 12.1.2. Правила игры таковы. Первый игрок прячет в кулаке од% ну из двух монет: 1 руб. или 5 руб., по своему выбору, а второй игрок пы% тается угадать, какая монета спрятана, и если угадывает, то получает эту монету, в противном случае платит первому игроку 3 руб.

Решение. Платежная матрица, очевидно, имеет вид

Прежде всего проверим, нет ли в игре седловой точки. Действительно, нижняя цена игры

α = max min aij =max{−1, −5} = −1,

i=1,2 j=1,2

а верхняя цена игры

β = min max aij =min{3, 3} =3 ,

j=1,2 i=1,2

т. е. α ≠β, и седловой точки (в чистых стратегиях) в игре нет. Пусть пер% вый игрок выбирает свою первую стратегию с вероятностью p, а вторую стратегию — соответственно с вероятностью (1 – p), т. е. первый игрок иг% рает со смешанной стратегией

122

p p = 1−p .

Обозначим νj (p) ожидаемый выигрыш первого игрока, если второй иг% рок при этом выберет свою j%ю стратегию. В нашем случае

ν1(p) =(−1)p +3(1−p) ,

ν2(p) =3p +(−5)(1−p) .

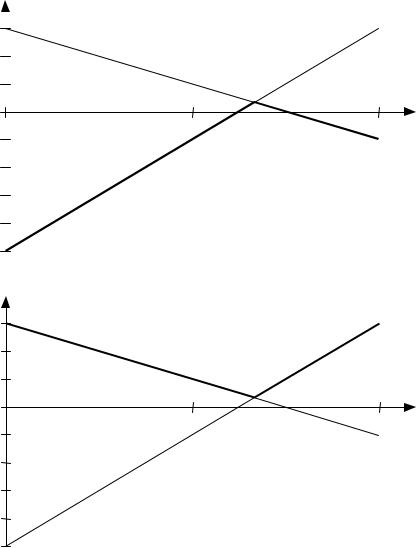
Построим графики этих функций на рис. 12.1.1, а.

–2

–3

–4

–5

б) верхняя граница проигрыша второго игрока в зависимости от его смешанной стратегии

Рис. 12.1.1. Гарантированный выигрыш первого игрока и верхняя граница проигрыша второго игрока в зависимости от смешанных стратегий

Второй игрок так выбирает свои стратегии, чтобы обеспечить первому минимальный выигрыш: ν(p) = min{ν1(p), ν2(p)} (эта функция отмечена на рис. 12.1.1, а жирной линией). Иными словами, второй игрок в любом слу%

123

α= max min aij =max{−2, −4} = −2 ,

i=1,2 j=1,2,3,4

а верхняя цена игры

β = min max aij =min{2, 3, 4, 1} =1,

j=1,2,3,4 i=1,2

т. е. α ≠β, значит, седловой точки (в чистых стратегиях) в игре нет. Пусть первый игрок выбирает свою первую стратегию с вероятностью p, а вто% рую стратегию — соответственно с вероятностью (1 – p), т. е. первый иг% рок играет со смешанной стратегией

Обозначим νj (p) ожидаемый выигрыш первого игрока, если второй иг% рок при этом выберет свою j%ю стратегию. В нашем случае

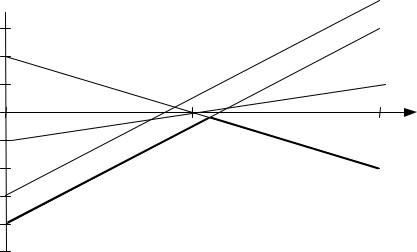
Графики этих функций построены на рис. 3.12.2.

Рис. 12.1.2. Гарантированный выигрыш первого игрока при различном выборе смешанной стратегии

Второй игрок так выбирает свои стратегии, чтобы обеспечить первому минимальный выигрыш: ν(p) = min{ν1(p), ν2(p),ν3 (p), ν4 (p)} (эта функция

отмечена на рис. 3.12.2 жирной линией). Иными словами, при p [0; p )

второй игрок будет выбирать свою вторую стратегию и первый игрок бу% дет выигрывать ν2 (p) , при p ( p ;1] второй игрок будет выбирать первую стратегию и первый игрок будет выигрывать ν1(p). Наилучший для пер%

вого игрока выбор при этом соответствует ν = max v(p) . В нашем случае

p [0;1]

оптимальной смешанной стратегией первого игрока является стратегия

125

При этом

Введем новые обозначения

xi = pi /ν, i =1, 2,…, m

и разделить все неравенства системы (12.1.2) на положительную цену иг% ры ν , то получим следующую систему:

При этом

Цель первого игрока — максимизировать цену игры, т. е. минимизиро%

m

вать величину 1/ν = ∑xi .

i=1

Таким образом, приходим к задаче линейного программирования для первого игрока:

Аналогичные рассуждения с позиции второго игрока приводят к задаче линейного программирования, двойственной к задаче для первого игрока:

Если оптимальные решения этих задач равны

127

то цена игры равна

Если же в платежной матрице есть отрицательные элементы или нули, то можно добавить ко всем элементам матрицы одно и тоже достаточно большое положительное число b, так чтобы все элементы матрицы стали положительными, затем поставить и решить пару двойственных задач линейного программирования, найти оптимальные смешанные стратегии игроков, а цену игры скорректировать путем вычитания из нее числа b.

ПРИМЕР 12.1.4. Решить матричную игру из примера 12.1.2 с помощью ее сведения к паре взаимно двойственных задач линейного программирования.

Решение. От платежной матрицы

путем добавления положительного числа b = 5 перейдем к матрице

все элементы которой положительны.

Пара двойственных задач линейного программирования такова:

Оптимальные решения этих задач равны

128

оптимальные смешанные стратегии игроков

а цена игры

12.2. З а д а н и е п р а к т и к у м а

Предприятие имеет две стратегии рыночного поведения, тогда как его конкурент имеет четыре таких стратегии. Прибыль (в млн. руб.), которую получит предприятие при условии, что оно изберет стратегию i (i = 1, 2), а его конкурент — стратегию j (j = 1, 2, 3, 4), равна aij. Платежная матрица Π для каждого варианта приведена в табл. 12.2.1.

Требуется двумя способами (графическим и с помощью сведения мат% ричной игры к паре взаимно двойственных задач линейного программи% рования) найти оптимальные смешанные стратегии предприятия и кон% курента, а также цену игры — оптимальную прибыль предприятия.

Т а б л и ц а 12.2.1

129