
Практикум по ИО
.pdfвыполняться лишь конечное число раз, поэтому указанный алгоритм обяза% тельно построит максимальный поток, и притом за конечное число шагов.
Следует обратить особое внимание на выполнение п. 3. Если по некото% рому пути μ мы пропустили поток величиной θ, то пропускные способности всех дуг этого пути следует уменьшить на θ, т. е. новая пропускная способ% ность дуги (Xi , Xj ) пути будет равна c′ij = cij −θ. Эта дуга может участво%
вать в последующем выборе нового пути, но с уменьшенной пропускной способностью. Поэтому вычисление новых пропускных способностей всех звеньев найденного пути совершенно необходимо. Кроме того, надо также учесть возможность существования вместо найденного пути другого, в ко% тором участвует некоторая дуга, симметричная одной из дуг предыдущего пути. Для этого пропускные способности всех дуг, симметричных дугам старого пути ν, следует увеличить на θ, т. е. пропускную способность дуги
(Xi , Xj ) , |
симметричной использованной в предшествующем пути дуге |
(Xi , Xj ) , |
надо считать равной c′ji = cji +θ. Это следует из того, что дуга |
(Xj , Xi ) |
не препятствует доставке в Xi количества cji вещества по новому |
пути с использованием этой дуги плюс количества θ по части старого пути от X0 до Xi без использования этой дуги (так как пропускная способность
всех дуг старого пути не меньше θ). Мы учитываем, что Xi теперь соеди% нена с X0 двумя путями, т. е. получается, что дуга (Xj , Xi ) как бы заменена новой дугой с увеличенной пропускной способностью c ji +θ.
Таким образом, процесс отыскания максимального потока в сети сво% дится к следующим действиям.
1.Построить произвольный путь μ из X0 в Xn , идущий по н е н а с ы %
ще н н ы м дугам.
2.Определить пропускную способность θμ найденного пути как наи% меньшую из пропускных способностей дуг этого пути
|
θμ = min{cμ |
}; |
(8.1.4) |
|
|
|
ij |
|
|
3. |
Вычислить новые пропускные способности всех дуг данного пути: |
|||
|
cμ |
= cμ −θμ |
; |
(8.1.5) |
|
ij |
ij |
|
|
4. |
Вычислить новые пропускные способности всех тех дуг, которые |
|||
симметричны дугам данного пути |
|
|
|
|
|
cμ |
= cμ +θμ |
; |
(8.1.6) |
|
ij |
ij |
|
|
5. |
Процесс, описанный в пп. 2—4, продолжается до тех пор, пока удается |
|||
построить путь из X0 в Xn , идущий по ненасыщенным дугам. Если такой путь построить нельзя, то это означает, что из источника X0 в сток Xn про% пущен максимальный поток. Затем следует вычесть пропускную способ% ность соответствующей дуги исходной сети. П о л о ж и т е л ь н ы е значе% ния найденных разностей определяют величины потоков по дугам в макси% мальном потоке данной сети, а величина максимального потока в сети равна
91
n |
n−1 |
w = ∑zoj |
= ∑zin . |
j=1 |
i=0 |
В заключение подчеркнем еще раз, что процесс преобразований пре% кращается, как только будет получена сеть, в которой нельзя построить ни одного пути из X0 в Xn , идущего по ненасыщенным дугам.
Покажем, что полученный таким образом поток является максималь% ным. Для этого построим в последней сети сечение (P,Q) следующим обра% зом. Ко множеству P отнесем источник X0 и все те вершины, которые дос% тижимы из X0 по какому%нибудь пути, составленному из ненасыщенных дуг, а все остальные вершины сети (недостижимые) отнесем к множеству Q. Очевидно, Xn Q, так как не существует никакого ненасыщенного пути
из X0 в Xn .
Все дуги сечения (P,Q) , направленные из P в Q, загружены полно% стью до пропускных способностей [т. е. для величины потока zij по дуге
(Xi , Xj ) при Xi P, Xj Q имеем zij |
= cij ], а дуги (Xj , Xi ) противоположного |
|
направления, идущие из Q в P , в построенном потоке не используются |
||
(т. е. zji =0 при Xj Q, Xi P ), так что величина потока равна |
||
w = ∑ zij − ∑ zji = ∑ cij =C(P,Q) , |
||
Xi P |
Xi P |
Xi P |
Xj Q |
Xj Q |
Xj Q |
т. е. построенный поток максимален, а (P,Q) — сечение с минимальной пропускной способностью (минимальное сечение).
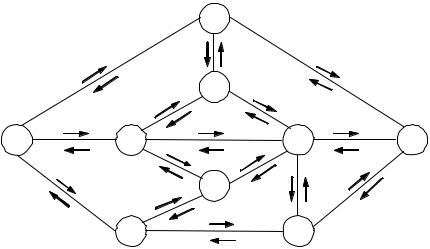
ПРИМЕР 8.1.1. Требуется определить максимальный поток в сети, изо% браженной на рис. 8.1.1, из вершины X0 в вершину X8 , где числа на дугах, снабженные стрелками, означают пропускные способности этих дуг в указанных направлениях.
Решение. В качестве начального возьмем нулевой поток, когда все
zij =0 .
Найдем какой%нибудь путь из X 0 в X8 , например, μ1 ={X0, X5, X8 } . По этому пути можно пропустить поток величиной не более
θ1 = min{c05, c58 } = min{5, 2} =2 .
Предположим, что поток такой величины 2 по указанному пути мы пропустили. Получили новый поток {z′ij } . При этом пропускные способно%
сти дуг пути и симметричных им дуг изменяются. Согласно (8.1.5) и (8.1.6) пропускные способности дуг пути уменьшаются на 2 единицы:
′ |
= c05 −θ1 =5 −2 =3, |
′ |
= c58 −θ1 =2 −2 =0 , |
c05 |
c58 |
т. е. дуга (X5, X8 ) становится насыщенной, а пропускные способности дуг, симметричных дугам пути, увеличиваются на 2 единицы:
c50′ = c50 +θ1 =4 +2 =6, c85′ = c85 +θ1 =2 +2 =0 .
92
X5
|
|
3 |
|
3 |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
X4 |
|
2 |
|
|
|
|
1 |
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
1 |
6 |
|
|
|
|
||||
|
|
|
|
|||
X0 |
X1 |
1 |
|
2 |
X6 |
X8 |
|
0 |
|
|
2 |
||
|
|
|
|
3 |
|
|
4 |
|
0 |
|
3 |
|
2 |
|
|
X3 |
2 |
2 |
2 |
|
|
|
|
|
|||
0 |
2 |
0 |
|
|
|
|
|
X2 |
3 |
|
|
X7 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
Рис. 8.1.1. Сеть в примере 8.1.1 |
|||||
Сеть с новыми |
пропускными |
способностями |
дуг приведена на |
|||
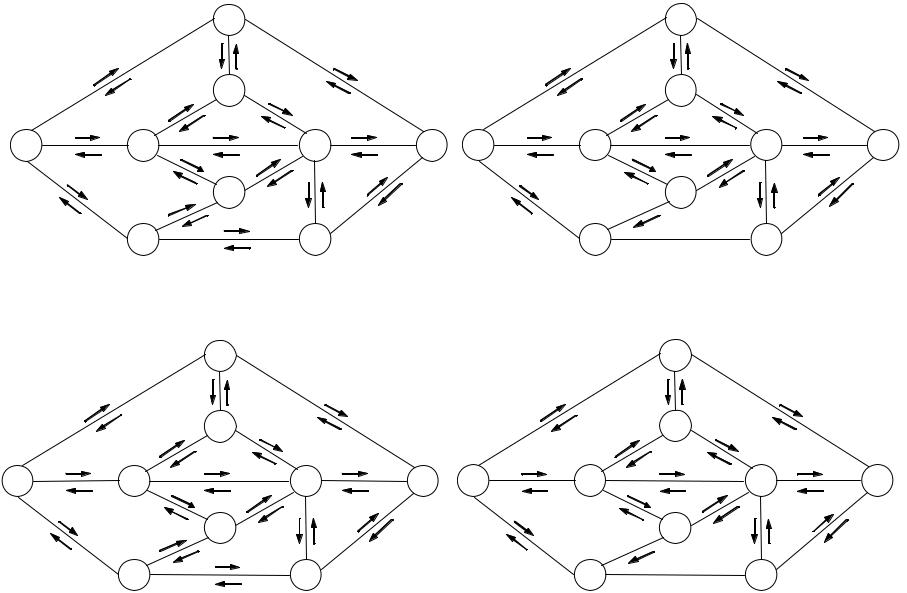
рис. 8.1.2, а. |
|
|
|
|
|
|
Теперь находим новый путь из X0 |
в X8 , проходящий по ненасыщенным |
|||||
дугам, например, μ2 ={X0, X5, X4, X6, X8 } , определяем |
|
|||||
θ2 = min{c05, c54, c46, c68 } = min{3, 3,1, 6} =1
и пропускаем по этому пути поток величиной в одну единицу. Меняем пропускные способности дуг этого пути и симметричных им дуг:
c05′′ = c05′ −θ2 =3 −1 =2, c50′′ = c50′ +θ2 =6 +1 =7, c54′′ = c54′ −θ2 =3 −1 =2, c45′′ = c45′ +θ2 =3 +1 = 4, c46′′ = c46′ −θ2 =1−1 =0, c64′′ = c64′ +θ2 =1+1 =2, c68′′ = c68′ −θ2 =6 −1 =5, c86′′ = c86′ +θ2 =2 +1 =3.
Дуга (X4, X6 ) становится насыщенной. Сеть с измененными пропускны% ми способностями приведена на рис. 8.1.2, б.
Далее последовательно находим пути μ3,μ4,μ5,μ6 и по ним пропускаем
потоки величиной θ3,θ4,θ5,θ6 |
соответственно: |
|
||
μ3 ={X0, X5, X4, X1, X6, X8 }, |
θ3 = min{2, 2, 1, 2, 5} =1 (рис. 8.1.2, в), |
|||
μ4 ={X0, X1, X6 |
, X8 |
}, |
θ4 = min{1, 1, 4} =1 |
(рис. 8.1.2, г), |
μ5 ={X0, X2, X7 |
, X8 |
}, θ5 = min{4, 3, 2} =2 |
(рис. 8.1.2, д), |
|
μ6 ={X0, X2, X3, X6, X8 }, |
θ6 = min{2, 2, 3, 3} =2 (рис. 8.1.2, е). |
|||
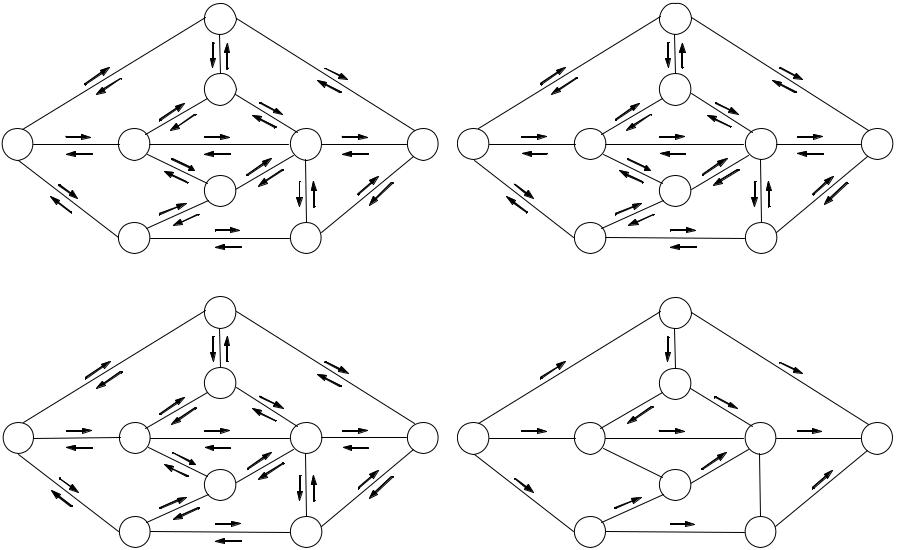
На указанных в скобках рисунках приведены сети, полученные после соответствующих преобразований на каждом шаге. В сети, изображенной на рис. 8.1.2, е, уже нельзя указать ни одного пути, идущего из X0 в X8 по ненасыщенным дугам. Следовательно, процесс преобразований закончен.
Чтобы определить максимальный поток, вычитаем от пропускных спо% собностей дуг исходной сети (рис. 8.1.1) измененные пропускные способ% ности тех же дуг последней сети (рис. 8.1.2, е). Результат приведен на рис. 8.1.2, ж.
93
94
X5
|
|
|
3 |
|
3 |
|
|
|
|
6 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
X4 |
|
|
4 |
|
|
|
|
1 |
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
1 |
|
6 |
|
|
|
|
||||
|
X1 |
|
|
X6 |
|||
X0 |
0 |
1 |
|
2 |
X8 |
||
|
|
|
|
2 |
|||
|
|
|
|
|
3 |
|
|
|
4 |
|
0 |
X3 |
3 |
|
2 |
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|||
|
0 |
2 |
0 |
|
|
|
|
|
|
X2 |
|
3 |
|
X7 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
а)
X5
|
|
|
2 |
|
4 |
|
|
|
|
7 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
X4 |
|
|
4 |
|
|
|
|
0 |
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
2 |
|
5 |
|
|
|
|
||||
|
|
|
|
|
|||
X0 |
0 |
X1 |
1 |
|
2 |
X6 |
X8 |
|
|
|
|
3 |
|||
|
|
|
|
|
3 |
|
|
|
4 |
|
0 |
X3 |
3 |
|
2 |
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|||
|
0 |
2 |
0 |
|
|
|
|
|
|
X2 |
|
3 |
|
X7 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
б)
|
|
|
X5 |
|
|
|
1 |
|
5 |
|
|
8 |
|
|
|
1 |
|
X4 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
0 |
|
|
X0 |
1 |
X1 |
|
4 |
|
1 |
|
||
|
2 |
0 |
X3 |
3 |
|
|
|
|
22  0
0
1 
X2
 4
4
д)
|
|
|
X5 |
|
|
|
1 |
|
5 |
|
|
8 |
|
|
|
1 |
|
X4 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
0 |
|
|
X0 |
1 |
X1 |
|
4 |
|
1 |
|
||
|
0 |
0 |
X3 |
1 |
|
|
|
|
40 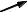 2
2
1 
X2
 4
4
е)
|
0 |
|
|
|
4 |
2 |
|
3 |
|
|
|
|
X6 |
X8 |
|
|
5 |
3 |
|
|
|
|
4 |
2 |
2 |
0 |
X7
|
0 |
|
|
|
4 |
2 |
|
1 |
|
|
|
|
X6 |
X8 |
|
|
7 |
5 |
|
|
|
|
4 |
2 |
2 |
0 |
X7
X5
15
|
|
8 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
X4 |
|
|
4 |
|
(+4) |
|
|
|
0 |
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
4 |
|
(+1) |
|
|
|
|
|||||
|
|
|
|
X0 |
||||
X0 |
0 |
X1 |
|
3 |
X6 |
X8 |
(–1) |
|
|
1 |
|
|
4 |
|
|||
|
|
|
|
3 |
|
|
|
|
|
4 |
0 |
X3 |
3 |
|
2 |
|
(+4) |
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||
|
0 |
2 |
0 |
|
|
|
|
(–4) |
|
|
X2 |
3 |
|
X7 |
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
в)
X5
15
|
|
8 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
X4 |
|
|
4 |
4 |
|
|
|
0 |
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
0 |
2 |
|
3 |
1 |
|
|
|
|||||
|
|
|
|
||||
X0 |
1 |
X1 |
|
4 |
X6 |
X8 |
X0 |
|
1 |
|
|
5 |
|
||
|
|
|
|
3 |
|
|
|
|
4 |
0 |
X3 |
3 |
|
2 |
4 |
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|||
|
0 |
2 |
0 |
|
|
|
|
|
|
X2 |
3 |
|
X7 |
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
X5
(+2) (–2)
(+2)
(–4)
|
|
X4 |
(+1) |
|
(–2) |
|
|
(+1) |
|
||||
|
|
|
|
|
||
(–1) |
(+2) |
|
|
(–1) |
(+5) |
|
|
|
|
||||
X2 |
|
|
(–2) |
|
X6 |
X8 |
0 |
|
|
|
|
(–5) |
|
|
|
|
(+2) |
(–2) |
(–2) |
|
|
0 |
X3 |
|
|
|
|
|
|
|
0 |
0 |
(+2) |
|
|
|
|
|
|||
(+2) |
(–2) |
|
|
|
|
|
X1 |
(+2) |
|
|
|
X7 |
|
|
|
(–2) |
|
|
||
|
|
|
|
|
|
|
|
|
ж) |
|
|
|
|
|
|
X5 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
X4 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
X1 |
|
|
|
|
X6 |
X8 |
|
|
|
2 |
|
|
|
|
|
X3 |
|
|
2 |
|
2 |
|
|
|
|
|
|
X2 |
2 |
|
|
|
X7 |
|
|
|
|
|
|
||
г) |
з) |
Рис. 8.1.2. Определение максимального потока в сети
95

Положительные значения найденных разностей дают нам величины zij
потоков по соответствующим дугам (Xi , Xj ) в максимальном потоке из ис% точника X0 в сток X8 . Искомый максимальной поток приведен на рис. 8.1.2, з, где числа, стоящие у каждой дуги, показывают величину по% тока по данной дуге, а стрелки — направление потока по этой дуге. Вели% чина максимального потока равна
wmax = θ1 +θ2 +θ3 +θ4 +θ5 +θ6 =2 +1+1+1+2 +2 =9
или, как видно из рис. 8.1.2, з,
wmax = z05 + z01 + z02 =4 +1+4 =9, wmax = z58 + z68 + z78 =2 +5 +2 =9.
Обычно процесс решения задачи записывают в виде последовательно% сти матриц изменяющихся пропускных способностей дуг сети. Чтобы не писать нулевые элементы этих матриц, удобно для каждого шага чертить соответствующую таблицу, оставляя пустыми те клетки, где должны стоять нули. Для исходной сети, приведенной на рис. 8.1.1, матрица про% пускных способностей дуг будет иметь вид табл. 8.1.1.
Т а б л и ц а 8.1.1 |
Т а б л и ц а 8.1.2 |
|
Xj |
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
Xi |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
|
|
1 |
4 |
|
|
5– |
|
|
|
X1 |
|
|
|
|
1 |
1 |
|
2 |
|
|
X2 |
|
|
|
|
2 |
|
|
|
3 |
|
X3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
X4 |
|
|
1 |
|
|
|
3 |
1 |
|
|
X5 |
|
4+ |
|
|
|
3 |
|
|
|
2– |
X6 |
|
|
2 |
|
3 |
1 |
|
|
2 |
6 |
|
|
|
|
|
||||||
X7 |
|
|
|
2 |
|
|
|
2 |
|
2 |
X8 |
|
|
|
|
|
|
2+ |
2 |
2 |
|
Xj |
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
Xi |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
X0 |
|
1 |
4 |
|
|
3– |
|
|
|
|
X1 |
|
|
|
1 |
1 |
|
2 |
|
|
|
X2 |
|
|
|
2 |
|
|
|
3 |
|
|
X3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
X4 |
|
|
|
|
|
3+ |
1– |
|
|
|
X5 |
6+ |
|
|
|
3– |
|
|
|
|
|
X6 |
|
2 |
|
3 |
1+ |
|
|
2 |
6– |
|
|
|
|
|
|||||||
X7 |
|
|
2 |
|
|
|
2 |
|
2 |
|
X8 |
|
|
|
|
|
4 |
2+ |
2 |
|
Чтобы по таблице пропускных способностей дуг сети, не имея рисунка сети, найти какой%нибудь путь из источника в сток, идущий по ненасы% щенным дугам, можно поступить следующим образом.
В нулевой строке таблицы выберем какой%нибудь элемент c0j, отличный от нуля, например, c05, стоящий в пятом столбце. Из вершины X0 можно перейти в X5. Для наглядности дугу (X0, X5) проведем прямо в нулевой строке таблицы из нулевого столбца в пятый, выделив начало дуги кру% жочком, конец — стрелкой. Теперь мы находимся в вершине X5. Чтобы зафиксировать это, сместимся по пятому столбцу до строки с тем же пя% тым номером и отметим эту клетку кружочком, а переход по вертикали
— пунктиром. В пятой строке имеются три ненулевых элемента соответ% ственно в нулевом, четвертом и восьмом столбцах. Это означает, что из X5 можно перейти или в X0 или в X4 или в X8. Возвращаться в X0 нет смысла,
96
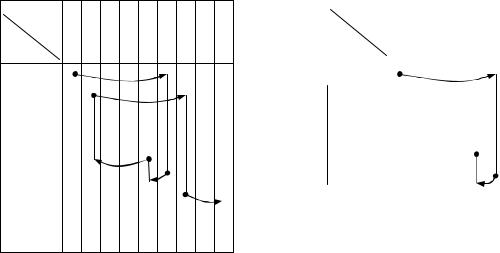
лучше всего идти в сток X8. Этот переход изображен стрелкой в пятой строке с началом в пятом столбце и концом — в восьмом.
Таким образом, по таблице мы нашли путь, ведущий по ненасыщенным дугам из источника в сток:
X0 → X5 → X6 .
Теперь по таблице надо указать пропускную способность найденного пути и изменить пропускные способности дуг этого пути и симметричных им дуг. Для этого отмечаем знаком «минус» числа в тех клетках, где нахо% дятся концы дуг, а числа в клетках, симметричных указанным относи% тельно главной диагонали, отмечаем знаком «плюс».
Пропускная способность найденного пути равна, очевидно, наимень% шему среди чисел, отмеченных знаком «минус»:
θ = min{cij− }.
В данном случае θ1 =2 .
Чтобы вычислить новые пропускные способности дуг найденного пути и симметричных им дуг, достаточно, согласно (8.1.5) и (8.1.6), из всех чисел, отмеченных знаком «минус», вычесть наименьшую пропускную способ% ность θ1 , а ко всем числам, отмеченным знаком «плюс», прибавить θ1 . Полу% чаем табл. 8.1.2 с измененными пропускными способностями дуг сети. Она соответствует рис. 8.1.1, а. По таблице находим путь
X0 → X5 → X4 → X6 → X8 ,
отмечаем знаком «минус» пропускные способности дуг этого пути (они записаны в клетках на концах стрелок), знаком «плюс» — пропускные способности симметричных дуг. Находим θ2 как наименьшее среди cij− .
Прибавляя θ2 к cij+ и вычитая из cij− , переходим к табл. 8.1.3 и т. д.
Т а б л и ц а 8.1.3 |
Т а б л и ц а 8.1.4 |
Xj X0 X1 X2 X3 X4 X5 X6 X7 X8
Xi
X0 |
|
1 4 |
|
|
|
2– |
|
|
||
X1 |
|
|
|
1 |
1+ 2– |
|
|
|||
X2 |
|
|
|
2 |
|
|
|
|
3 |
|
X3 |
|
|
|
|
3 |
|
|
|||
X4 |
|
1– |
|
|
4 |
|
|
|
||
X5 |
7+ |
|
|
|
2– |
|
|
|
|
|
X6 |
2+ |
|
3 |
2 |
|
|
|
2 |
5– |
|
X7 |
2 |
|
2 |
|
2 |
|||||
X8 |
|
|
|
|
4 3+ |
2 |
|
|||
|
Xj |
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
Xi |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
|
|
|
|
|
|
1 |
|
|
|
X1 |
|
1 |
|
|
1 |
2 |
|
|
|
|
X2 |
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
X3 |
|
|
|
2 |
|
|
|
1 |
|
|
X4 |
|
|
|
|
|
|
5 |
|
|
|
X5 |
|
8 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
X6 |
|
|
4 |
|
5 |
2 |
|
|
2 |
1 |
X7 |
|
|
|
4 |
|
|
|
2 |
|
|
X8 |
|
|
|
|
|
|
4 |
7 |
4 |
|
|
|
|
|
|
|
|
Выполнив еще четыре шага, придем к табл. 8.1.4. Из этой таблицы вид% но, что не существует ни одного пути из источника в сток. Действительно, из X0 можно перейти в X5. Далее, так как в пятой строке только два нену% левых элемента c50 и c54, можно перейти либо в X0 (вернуться, что бес%
97

смысленно), либо в X4. Но в четвертой строке только один элемент c45, от% личный от нуля. Поэтому из вершины X4 можно перейти только в X5, т. е. опять появляется контур. Никаких других возможностей нет. Следова% тельно, увеличить поток нельзя.
Для определения полученного максимального потока вычитаем из эле% ментов первой таблицы (см. табл. 8.1.1) соответствующие элементы по% следней (см. табл. 8.1.4). Записывая только положительные из найденных разностей, получаем табл. 8.1.5, указывающую максимальный поток в за% данной сети с величиной
w* = z58 + z68 + z78 =2 +5 +2 =9 .
Т а б л и ц а 8.1.5
Xj |
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
Xi |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
X0 |
|
1 |
4 |
|
|
4 |
|
|
|
|
X1 |
|
|
|
|
|
|
2 |
|
|
|
X2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
X3 |
|
|
|
|
|
|
2 |
|
|
|
X4 |
|
1 |
|
|
|
|
1 |
|
|
|
X5 |
|
|
|
|
2 |
|
|
|
2% |
|
|
|
|
|
|
|
|
||||
X6 |
|
|
|
|
|
|
|
|
5 |
|
X7 |
|
|
|
|
|
|
|
|
2 |
|
X8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть дан граф Γ(X, U) . Каждой дуге графа поставим в соответствие положительное число l(u). Это число можно назвать длиной дуги. Тогда за длину пути μ принимается сумма дуг, входящих в μ,
L(μ) = ∑l(u).
uμ
В задаче о кратчайшем пути требуется на графе Г найти кратчайший путь —путь наименьшей длины из вершины X0 в вершину Xn.
АЛГОРИТМ ОПРЕДЕЛЕНИЯ КРАТЧАЙШЕГО ПУТИ (АЛГОРИТМ ДЕЙКСТРЫ).
1. |
Присвоить каждой вершине Xi метку λi так, чтобы λ0 = 0, λi = +∞ |
(i > 0). |
|
2. |
Найти дугу u = uij = (Xi, Xj), для которой выполняется неравенство |
λj – λi > l(uij) (полагая, что ∞ – ∞ = 0). Заменить метку вершины xj на но% вую, меньшую метку λj = λi + l(uij).
3. П. 2 применять до тех пор, пока для каждой дуги uij не станет спра% ведливым неравенство λj −λi l(uij ) .
4. Найти вершину Xk, из которой выходит дуга, приходящая в Xn, и для которой λn = λk + l(ukn), затем вершину Xm, из которой выходит дуга, при% ходящая в Xk, и для которой λk = λm + l(umk) и т. д. На некотором шаге Xp
98
совпадет с вершиной X0. Путь μ = (Xp, …, Xm, Xk, Xn) будет кратчайшим, а его длина будет равна λn.
Внекоторых моделях возникает задача о нахождении не самого корот% кого, а наоборот, самого длинного пути между двумя заданными верши% нами графа.
Взадаче о критическом пути требуется на графе Г найти критиче5
ский путь — путь наибольшей длины из вершины X0 в вершину Xn.
Если рассмотреть сетевой график, дуги которого соответствуют работам, запланированным по некоторому проекту, а метка каждой дуги равна за% планированному времени выполнения соответствующей работы, то крити% ческий путь состоит из работ, замедление каждой из которых влияет на время выполнение всего проекта. Менеджер проекта должен особое внима% ние обращать на своевременное выполнение работ критического пути.
Предлагаем студенту самостоятельно построить алгоритм определения критического пути по аналогии с алгоритмом определения кратчайшего пути.
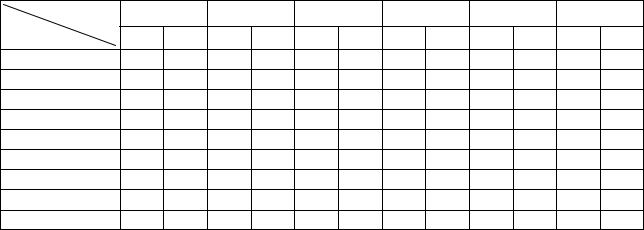
ПРИМЕР 8.1.2. Требуется определить кратчайший путь из вершины X0 в
вершину X8 в графе, изображенном на рис. 8.1.3, а, где числа на дугах озна% чают длины этих дуг.
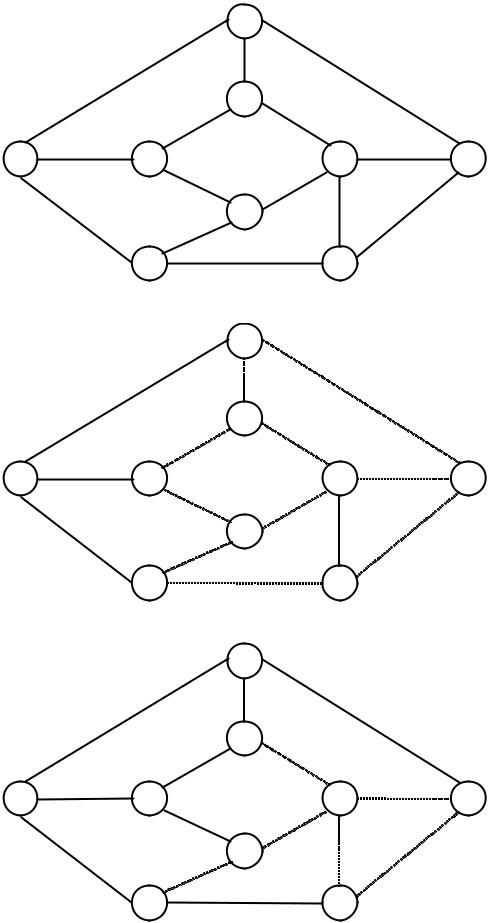
Решение. Решение задачи по приведенному алгоритму иллюстрируется табл. 8.1.6 и рис. 8.1.3, б — е.
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
8.1.6 |
||
Шаг |
1 |
|
2 |
|
|
3 |
|
4 |
5 |
|
|
6 |
Вершина |
λ |
Xi – 1 |
λ |
Xi – 1 |
λ |
Xi – 1 |
λ |
Xi – 1 |
λ |
Xi – 1 |
λ |
Xi – 1 |
X0 |
0 |
X0 |
0 |
X0 |
0 |
X0 |
0 |
X0 |
0 |
X0 |
0 |
X0 |
X1 |
+ |
— |
1 |
X0 |
1 |
X0 |
1 |
X0 |
1 |
X0 |
1 |
X0 |
X2 |
+ |
— |
4 |
X0 |
4 |
X0 |
4 |
X0 |
4 |
X0 |
4 |
X0 |
X3 |
+ — + — 2 X1 |
2 |
X1 |
2 |
X1 |
2 |
X1 |
|||||
X4 |
+ — + — 2 X1 |
2 |
X1 |
2 |
X1 |
2 |
X1 |
|||||
X5 |
+ |
— |
5 |
X0 |
5 |
X0 |
5 |
X0 |
5 |
X0 |
5 |
X0 |
X6 |
+ — + — + — 3 X3 |
3 |
X3 |
3 |
X3 |
|||||||
X7 |
+ — + — 7 X2 |
7 |
X2 |
5 |
X6 |
5 |
X6 |
|||||
X8 |
+ — + — 8 X5 |
8 |
X5 |
8 |
X5 |
7 |
X7 |
|||||
На этих рисунках пунктиром отмечены проверенные, но не перспектив% ные пути (имеющие длину большую, чем кратчайший путь из вершины X0
в данную вершину, а рядом с дугами, приходящими в вершины, написаны метки соответствующих вершин (т. е. длины самых кротких путей из X0 в
данную вершину).
На последнем шаге (рис. 8.1.3, е) получены кратчайшие пути из вершины X0 во все остальные, в том числе, и кратчайший путь из X0 в X8 :
X0 → X1→ X4 → X6 → X7 → X8 .
Длина этого пути равна
1 + 1 + 1 + 2 + 2 = 7.
99
X5
3
|
5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
X4 |
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
6 |
|
|
|
|
|
||
X0 |
X1 |
|
|
X6 |
X8 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
4 |
|
X3 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
||
|
|
|
2 |
|
|
|
X2 |
|
3 |
X7 |
|
|
|
|
|
||
|
|
|
а) |
|
|
|
|
|
X5 |
|
|
|
5 |
|
|
|
|
|
|
|
X4 |
|
|
|
1 |
|
|
|
|
X0 |
X1 |
|
|
X6 |
X8 |
|
4 |
|
X3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
X2 |
|
|
X7 |
|
|
|
|
б) |
|
|
|
|
|
X5 |
|
|
|
5 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
X4 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
X0 |
X1 |
|
|
X6 |
X8 |
2
4
X3
X2 |
7 |
X7 |
в)
Рис. 8.1.3. Определение кратчайшего пути
100
