
Практикум по ИО
.pdf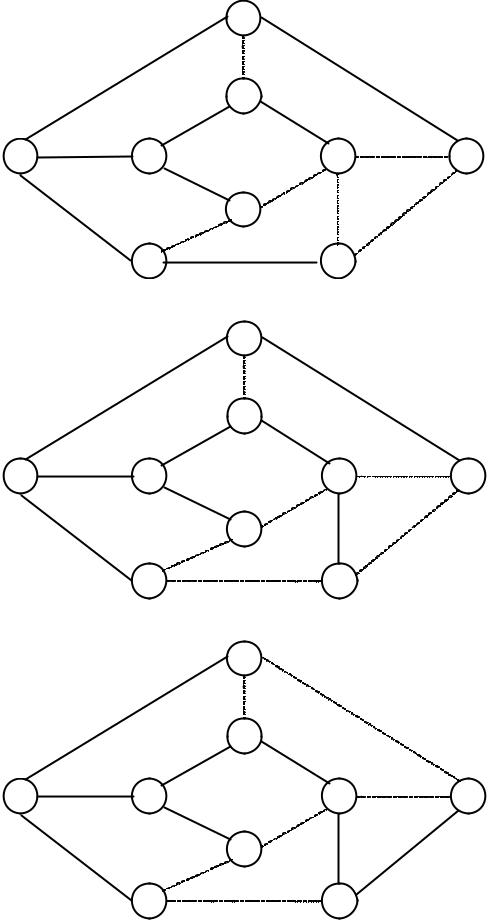
X5
|
5 |
|
8 |
|
|
|
|
|
X4 |
|
|
|
2 |
3 |
|
|
|
|
|
|
1 |
|
|
X0 |
X1 |
X6 |
X8 |
|
2 |
|
|
|
4 |
|
|
|
X3 |
|
|
|
2 |
|
|
|
7 |
X7 |
|
|
X2 |
|
|
|
г) |
|
|
|
X5 |
|
|
|
5 |
|
8 |
|
|
|
|
|
X4 |
|
|
|
2 |
3 |
|
|
|
|
|
|
1 |
|
|
X0 |
X1 |
X6 |
X8 |
|
2 |
|
|
|
4 |
5 |
|
|
X3 |
|
|
|
2 |
|
|
|
X2 |
X7 |
|
|
д) |
|
|
|
X5 |
|
|
|
5 |
|
|
|
X4 |
|
|
|
2 |
3 |
|
|
|
|
|
|
1 |
|
|
X0 |
X1 |
X6 |
X8 |
|
2 |
|
|
|
4 |
|
|
|
X3 |
5 |
7 |
|
2 |
|
|
|
X2 |
X7 |
|
е)
101
8.2.З а д а н и я п р а к т и к у м а
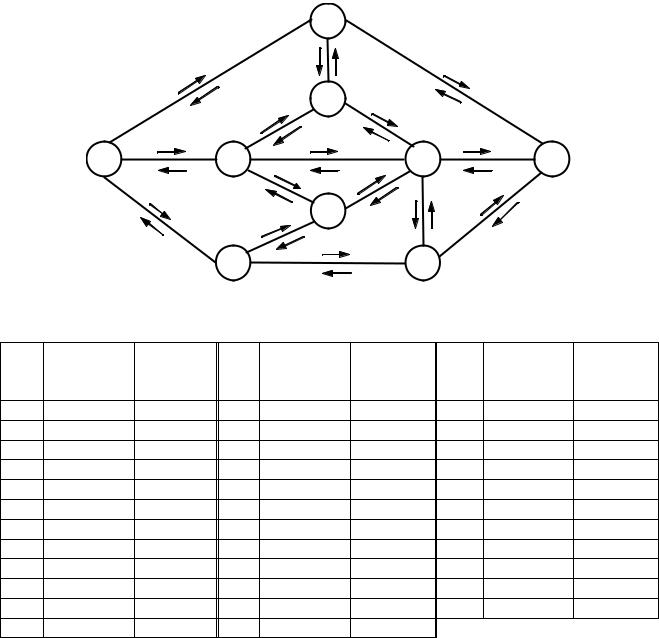
1.ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ В СЕТИ. Требуется определить макси%
мальный поток в сети, приведенной на рис. 8.2.1, из вершины Xi в вершину Xj, где числа на дугах, снабженные стрелками, означают пропускные спо% собности этих дуг в указанных направлениях. Номера вершин i и j для каждого варианта приведены в табл. 8.2.1.
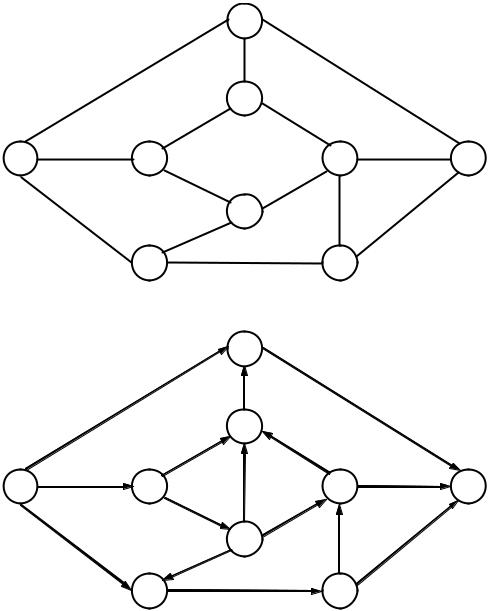
2.ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ. Требуется определить кратчайший путь из
вершины Xi в вершину Xj в графе, приведенном на рис. 8.2.2, где числа на дугах означают длины этих дуг. Номера вершин i и j для каждого варианта приведены в табл. 8.2.1.
3.ЗАДАЧА О КРИТИЧЕСКОМ ПУТИ. Требуется определить критический путь
из вершины Xi в вершину Xj в сетевом графике, приведенном на рис. 8.2.3, где числа на дугах равны продолжительностям соответствующих этим ду% гам работ инвестиционного проекта. Номера вершин i и j для каждого ва% рианта приведены в табл. 8.2.1.
X5
33
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
X4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
X0 |
X1 |
|
X6 |
|
X8 |
|
|
|||
|
5 |
3 |
2 |
|
|
|
|
||||
|
|
|
3 |
|
|
4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
3 |
|
|
|
1 |
|
|
|
|
|
|
X3 |
|
3 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
X2 |
3 |
|
X7 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.2.1. Сеть для определения максимального потока |
|
|
||||||||
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
8.2.1 |
|
№ |
Начальная |
Конечная |
№ |
Начальная |
Конечная |
|
№ |
Начальная |
Конечная |
||
|
|
вершина |
|||||||||
вар. |
вершина i |
вершина j |
вар. |
вершина i |
|
вершина j |
|
вар. |
вершина i |
|
|
|
|
|
j |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
2 |
13 |
1 |
|
7 |
|
25 |
4 |
|
8 |
2 |
0 |
3 |
14 |
1 |
|
8 |
|
26 |
6 |
|
5 |
3 |
0 |
4 |
15 |
2 |
|
4 |
|
27 |
6 |
|
8 |
4 |
0 |
5 |
16 |
2 |
|
5 |
|
28 |
7 |
|
4 |
5 |
0 |
6 |
17 |
2 |
|
6 |
|
29 |
7 |
|
5 |
6 |
0 |
7 |
18 |
2 |
|
7 |
|
30 |
7 |
|
8 |
7 |
0 |
8 |
19 |
2 |
|
8 |
|
31 |
7 |
|
6 |
8 |
1 |
2 |
20 |
3 |
|
2 |
|
32 |
3 |
|
6 |
9 |
1 |
3 |
21 |
3 |
|
4 |
|
33 |
4 |
|
5 |
10 |
1 |
4 |
22 |
3 |
|
5 |
|
34 |
6 |
|
4 |
11 |
1 |
5 |
23 |
3 |
|
7 |
|
35 |
7 |
|
6 |
12 |
1 |
6 |
24 |
3 |
|
8 |
|
|
|
|
|
102
X5
3
|
5 |
|
|
3 |
|
|
|
|
|
|
|
X4 |
|
|
|
|
2 |
2 |
|
|
1 |
|
5 |
|
|
|
|
||
X0 |
X1 |
|
X6 |
X8 |
|
|
3 |
1 |
|
|
|
|
|
|
|
3 |
X3 |
|
|
|
|
2 |
3 |
|
|
|
|
||
|
|
4 |
|
|
|
X2 |
4 |
X7 |
|
|
|
|
||
|
Рис. 8.2.2. Граф для определения кратчайшего пути |
|||
|
|
X5 |
|
|
|
|
3 |
|
|
|
5 |
|
|
3 |
|
|
|
|
|
|
|
X4 |
|
|
|
|
2 |
2 |
|
|
1 |
|
5 |
|
|
|
|
||
X0 |
X1 |
2 |
X6 |
X8 |
|
|
3 |
1 |
|
|
|
|
|
|
|
3 |
X3 |
|
|
|
|
2 |
3 |
|
|
|
|
||
|
|
4 |
|
|
|
X2 |
4 |
X7 |
|
|
|
|
||
Рис. 8.2.2. Сетевой график для определения критического пути
103

9. ОПТИМАЛЬНОСТЬ ПО ПАРЕТО
9.1. К р а т к и е т е о р е т и ч е с к и е с в е д е н и я и у к а з а н и я к в ы п о л н е н и ю з а д а н и й
Обозначим буквой E некоторую обобщенную характеристику произ% вольной инвестиционной операции, которую назовем эффективностью операции (в качестве E можно взять доход, доходность в процентах от вложенной суммы, доходность в процентах годовых, внутреннюю норму доходности и т. п.). Часто невозможно заранее точно предсказать эффек% тивность той или иной операции, и такие операции рассматривают как с л у ч а й н ы е в е л и ч и н ы. При этом в качестве ожидаемой эффек5 тивности такой инвестиционной операции используют м а т е м а т и % ч е с к о е о ж и д а н и е ME случайной величины E.
Под риском инвестиционных операций мы понимаем отклонение ре% альных значений эффективности инвестиционной операции от прогнози% руемой эффективности (как в меньшую сторону, так и в бόльшую).
Если E — случайная эффективность инвестиционной операции, и в ка% честве ожидаемой эффективности операции мы выбрали математическое ожидание ME случайной величины E, то в качестве измерителя риска
операции естественно взять |
с р е д н е е к в а д р а т и ч н о е о т к л о % |
н е н и е |
|
|
σE = DE |
(здесь DE — д и с п е р с и я |
случайной величины E). |
Знание только математических ожиданий и средних квадратичных от% клонений случайных величин довольно%таки важно при анализе группы случайных величин, оно помогает выбрать из множества случайных ве% личин оптимальные по Парето, отбросив заведомо «плохие».
Пусть на финансовом рынке существует возможность осуществить не% сколько инвестиционных операций, ожидаемые эффективности и риски которых известны и равны соответственно ME1, ME2, … , MEn и σ1, σ2, … , σn. Говорят, что i%я операция доминирует j%ю, если
|
|
MEj , |
|
>MEj , |
MEi |
MEi |
|||
|
< σj |
|
или |
σj . |
σi |
|
σi |
||
|
|
|
|
|
Операция называется оптимальной по Парето, если не существует операций, которые бы ее доминировали.
ПРИМЕР 9.1.1. Инвестор рассматривает четыре инвестиционные опера% ции со случайными эффективностями, описываемыми случайными вели% чинами E1, E2, E3, E4 с рядами распределения
E1 |
2 |
5 |
8 |
4 |
, |
E2 |
2 |
3 |
4 12 |
, |
|
p |
1/6 |
1/2 |
1/6 |
1/6 |
|
p |
1/2 |
1/6 |
1/6 1/6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
104
E3 |
3 |
5 |
8 10 |
, |
E4 |
1 |
2 |
4 |
8 |
. |
|
p |
1/6 |
1/6 |
1/2 1/6 |
|
p |
1/2 |
1/6 |
1/6 |
1/6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Требуется определить, какие из этих операций оптимальны по Парето. Решение. Ожидаемые эффективности и риски равны соответственно
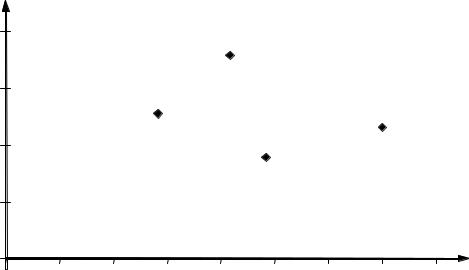
ME1 = 4,81, σ1 = 1,77, ME2 = 4,16, σ2 = 3,57, ME3 = 7,00, σ3 = 2,30, ME4 = 2,81, σ4 = 2,54. Нанесем точки (MEi; σi) на единый график (рис. 9.1.1). i%я опера%
ция доминирует j%ю, если точка, соответствующая i%й операции, нахо% дится на графике правее и ниже точки, соответствующей j%й операции.
Видно, что первая операция доминирует вторую и четвертую, третья операция также доминирует вторую и четвертую. При этом первая опе% рация не доминирует третью, а третья не доминирует первую. Первая и третья операции, таким образом, оптимальны по Парето.
Отметим, что операции, оптимальные по Парето, не обязательно явля% ются «самыми лучшими» (и даже просто «хорошими») — эти операции н е я в л я ю т с я х у д ш и м и. Выбор операций среди оптимальных по Парето осуществляется на основе склонности лица, принимающего соот% ветствующее решение, к риску.
σi
4
|
|
|
|
2 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MEi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Рис. 9.1.1. График «риск — доходность» |
|
|||||
В некоторых ситуациях предпочтительной оказывается операция, в которой ожидаемая эффективность вообще отрицательна. Например, если перед нами стоит выбор из двух операций:
•потерять 1 руб.;
•с вероятностью 0,5 получить 1 000 000 руб. и с вероятностью 0,5 поте% рять 100 000 руб.,
то обе эти операции окажутся оптимальными по Парето (ME1 = –1, σ1 = 0, ME2 = 550 000, σ2 = 450 000), но, скорее всего, мы склонимся к выбору первой операции, несмотря на то, что ожидаемый доход по ней составляет отрицательное число (–1 руб.), тогда как ожидаемый доход от исполнения второй операции составляет 550 000 руб. — слишком велик риск у второй операции, слишком велика вероятность потерь.
105
Рассмотренный подход может быть применен и при анализе других задач многокритериальной оптимизации.
В произвольной задаче выбора операции по нескольким критериям операция i доминирует операцию j, если операция i по каждому из кри% териев н е х у ж е операции j и хотя бы по одному из критериев — с т р о г о л у ч ш е.
Операция i называется оптимальной по Парето, если не существует операций, которые бы ее доминировали.
Например, в ситуации с частичной неопределенностью можно рассмотреть в качестве критериев ожидаемый доход MQ (операция i не хуже операции j по этому критерию, если MQi MQj, и лучше операции j по этому критерию, если MQi > MQj) и ожидаемые сожаления MR (операция i не хуже операции j по этому критерию, если MRi MRj, и лучше операции j по этому критерию, если MRi < MRj).
9.2. З а д а н и е п р а к т и к у м а
Инвестор рассматривает четыре инвестиционные операции со случай% ными эффективностями, описываемыми случайными величинами En, En + 1, E n + 2 и E n + 3 (где n —номер варианта) с рядами распределения, приведен% ными в табл. 9.2.1. Требуется определить, какие из этих операций опти% мальны по Парето.
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
9.2.1 |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
№ операции |
|
Ряд распределения |
№ операции |
|
Ряд распределения |
|
||||||||
|
|
|
эффективности |
|
|
|
эффективности |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
E1 |
|
0 |
2 |
4 |
16 |
12 |
E12 |
|
2 |
4 |
6 |
18 |
|
|
p |
|
1/2 |
1/4 |
1/8 |
1/8 |
p |
|
1/2 |
1/4 |
1/8 |
1/8 |
|
||
|
|
|
|
|
|
||||||||||
|
2 |
E2 |
|
0 |
4 |
6 |
12 |
13 |
E13 |
|
2 |
6 |
8 |
14 |
|
|
p |
|
1/4 |
1/4 |
1/3 |
1/6 |
p |
|
1/4 |
1/4 |
1/3 |
1/6 |
|
||
|
|
|
|
|
|
||||||||||
|
3 |
E3 |
|
0 |
1 |
2 |
8 |
14 |
E14 |
|
2 |
3 |
4 |
10 |
|
|
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
||
|
|
|
|
|
|
||||||||||
|
4 |
E4 |
|
0 |
4 |
6 |
10 |
15 |
E15 |
|
2 |
6 |
8 |
12 |
|
|
p |
|
1/5 |
1/5 |
1/5 |
2/5 |
p |
|
1/5 |
1/5 |
1/5 |
2/5 |
|
||
|
|
|
|
|
|
||||||||||
|
5 |
E5 |
|
0 |
1 |
5 |
14 |
16 |
E16 |
|
2 |
4 |
6 |
18 |
|
|
p |
|
1/5 |
2/5 |
1/5 |
1/5 |
p |
|
1/5 |
2/5 |
1/5 |
1/5 |
|
||
|
|
|
|
|
|
||||||||||
|
6 |
E6 |
|
0 |
8 |
16 |
20 |
17 |
E17 |
|
2 |
12 |
18 |
22 |
|
|
p |
|
1/2 |
1/8 |
1/8 |
1/4 |
p |
|
1/2 |
1/8 |
1/8 |
1/4 |
|
||
|
|
|
|
|
|
||||||||||
|
7 |
E7 |
|
0 |
4 |
10 |
14 |
18 |
E18 |
|
2 |
6 |
12 |
20 |
|
|
p |
|
1/4 |
1/4 |
1/4 |
1/4 |
p |
|
1/4 |
1/4 |
1/4 |
1/4 |
|
||
|
|
|
|
|
|
||||||||||
|
8 |
E8 |
|
0 |
4 |
5 |
20 |
19 |
E19 |
|
2 |
6 |
8 |
12 |
|
|
p |
|
1/2 |
1/4 |
1/5 |
1/20 |
p |
|
1/2 |
1/4 |
1/5 |
1/20 |
|
||
|
|
|
|
|
|
||||||||||
|
9 |
E9 |
|
0 |
4 |
8 |
32 |
20 |
E20 |
|
–6 |
–4 |
–2 |
10 |
|
|
p |
|
1/2 |
1/4 |
1/8 |
1/8 |
p |
|
1/2 |
1/4 |
1/8 |
1/8 |
|
||
|
|
|
|
|
|
||||||||||
|
10 |
E10 |
|
0 |
8 |
12 |
24 |
21 |
E21 |
|
–6 |
–2 |
0 |
–6 |
|
|
p |
|
1/4 |
1/4 |
1/3 |
1/6 |
p |
|
1/4 |
1/4 |
1/3 |
1/6 |
|
||
|
|
|
|
|
|
||||||||||
|
11 |
E11 |
|
0 |
2 |
4 |
16 |
22 |
E22 |
|
–6 |
–5 |
–4 |
3 |
|
|
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
||
|
|
|
|
|
|
||||||||||
106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

О к о н ч а н и е т а б л. 9.2.1
№ операции |
|
Ряд распределения |
||||
|
|
эффективности |
|
|||
|
|
|
|
|||
23 |
E23 |
|
0 |
8 |
12 |
20 |
p |
|
1/5 |
1/5 |
1/5 |
2/5 |
|
|
|
|||||
24 |
E24 |
|
0 |
2 |
10 |
28 |
p |
|
1/5 |
2/5 |
1/5 |
1/5 |
|
|
|
|||||
25 |
E25 |
|
0 |
16 |
32 |
40 |
p |
|
1/2 |
1/8 |
1/8 |
1/4 |
|
|
|
|||||
26 |
E4 |
|
0 |
8 |
20 |
28 |
p |
|
1/4 |
1/4 |
1/4 |
1/4 |
|
|
|
|||||
27 |
E26 |
|
0 |
8 |
10 |
40 |
p |
|
1/2 |
1/4 |
1/5 |
1/20 |
|
|
|
|||||
28 |
E27 |
|
0 |
2 |
4 |
16 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
|
|
|||||
29 |
E28 |
|
0 |
8 |
12 |
20 |
p |
|
1/5 |
1/5 |
1/5 |
2/5 |
|
|
|
|||||
30 |
E29 |
|
0 |
3 |
6 |
12 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
|
|
|||||
31 |
E30 |
|
0 |
8 |
15 |
20 |
p |
|
1/2 |
1/4 |
1/5 |
1/20 |
|
|
|
|||||
№ операции |
|
Ряд распределения |
||||
|
|
эффективности |
|
|||
|
|
|
|
|||
31 |
E31 |
|
–6 |
–2 |
0 |
4 |
p |
|
1/5 |
1/5 |
1/5 |
2/5 |
|
|
|
|||||
32 |
E32 |
|
–6 |
–5 |
–1 |
8 |
p |
|
1/5 |
2/5 |
1/5 |
1/5 |
|
|
|
|||||
33 |
E33 |
|
–6 |
2 |
10 |
14 |
p |
|
1/2 |
1/8 |
1/8 |
1/4 |
|
|
|
|||||
34 |
E34 |
|
–6 |
–2 |
4 |
8 |
p |
|
1/4 |
1/4 |
1/4 |
1/4 |
|
|
|
|||||
35 |
E35 |
|
–6 |
–2 |
–1 |
14 |
p |
|
1/2 |
1/4 |
1/5 |
1/20 |
|
|
|
|||||
36 |
E36 |
|
–6 |
–5 |
–4 |
3 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
|
|
|||||
37 |
E37 |
|
–6 |
–4 |
–2 |
10 |
p |
|
1/2 |
1/4 |
1/8 |
1/8 |
|
|
|
|||||
38 |
E38 |
|
–6 |
–3 |
–2 |
6 |
p |
|
1/3 |
1/3 |
1/6 |
1/6 |
|
|
|
|||||
|
|
|
|
|
|
|
107
10. МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ
10.1. К р а т к и е т е о р е т и ч е с к и е с в е д е н и я и у к а з а н и я к в ы п о л н е н и ю з а д а н и й
Задачи многокритериальной, или векторной, оптимизации возника% ют в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость, надежность и т. п.). Требуется найти точку области допустимых решений, которая миними% зирует или максимизирует все эти критерии. Обозначим i%й частный критерий через zi (x), а область допустимых решений через Q. Учтем, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации, и наоборот, мы можем сформулировать кратко за% дачу векторной оптимизации следующим образом:
z (x) |
|
|
|
z1 (x) |
|
→max , |
(10.1.1) |
z(x) = 2 |
|
||
|
|
|
|
zm (x) |
|
|
|
x Q . |
(10.1.2) |
||
В идеальном случае в задаче (10.1.1)—(10.1.2) можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных ре% шений всех однокритериальных задач. Но указанное пересечение обычно оказывается пустым множеством, и потому приходится рассматривать пе5 реговорное множество — множество допустимых решений [т. е. удовле% творяющих требованию (10.1.2)], оптимальных по Парето.
Метод последовательных уступок решения многокритериальных за% дач применяется в случае, когда частные критерии могут быть упорядо% чены в порядке убывающей важности. Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение z1* , первого по важности критерия в об% ласти допустимых решений, решив задачу
z1(x) →max, x Q.
Затем назначается, исходя из практических соображений и принятой точ% ности, величина допустимого отклонения δ1 >0 (экономически оправданной уступки) критерия z1 и отыскивается максимальное значение второго крите% рия z2 при условии, что значение первого должно отклоняться от максималь% ного не более чем на величину допустимой уступки, т. е. решается задача
z2(x) →max,
z (x) |
z* |
−δ |
, |
1 |
1 |
1 |
|
x Q.
108
Снова назначается величина уступки δ2 >0 по второму критерию, ко% торая вместе с первой используется при нахождении условного экстре% мума третьего частного критерия, и т. д. Наконец, выявляется экстре% мальное значение последнего по важности критерия z2 при условии, что значение каждого из первых m – 1 частных критериев отличается от экс% тремального не более чем на величину допустимой уступки. Получаемое на последнем этапе решение считается о п т и м а л ь н ы м. Остается за% метить, что этот метод не всегда приводит к эффективному решению.
ПРИМЕР 3.10.1. Дана задача векторной оптимизации:
z1 |
= −x1 +2x2 →max , |
|
||
z2 =2x1 + x2 →max , |
(10.1.3) |
|||
z1 |
= −x1 +2x2 →max , |
(10.1.4) |
||
|
x + x |
6, |
|
|
|
1 |
2 |
3, |
(10.1.5) |
|
1 |
x1 |
||
|
|
x2 |
4. |
|
|
1 |
|
||
Требуется определить переговорное множество, а затем решить дан% ную задачу методом последовательных уступок (допустимые уступки по первым двум критериям принять равными δ1 =3 и δ2 =5/3 ).
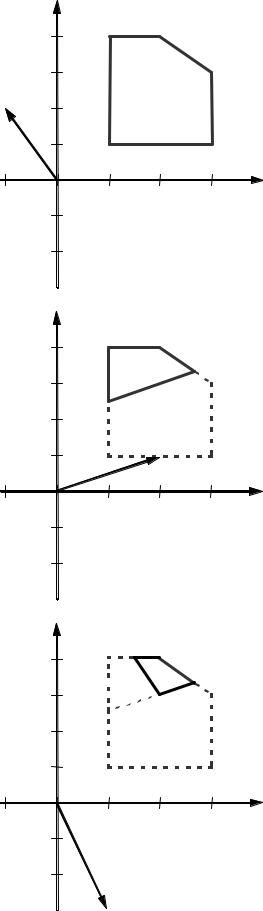
Решение. Очевидно, в данной задаче переговорное множество совпадает с областью допустимых решений (т. е. точек, удовлетворяющих условиям (10.1.5), они соответствуют пятиугольнику ABCDE на рис. 10.1.1, а). Дейст% вительно, возьмем любую точку множества допустимых решений. Если мы от нее сдвинемся вправо, то значения критериев z2 и z3 увеличатся, но значение критерия z1 уменьшится. Если мы сдвинемся левее, то значения критериев z2 и z3 уменьшатся, но значение критерия z1 увеличится. Если мы сдвинемся ниже, то значения критериев z1 и z2 увеличатся, но значе% ние критерия z3 уменьшится. Если мы сдвинемся выше, то значения кри% териев z1 и z2 уменьшатся, но значение критерия z3 увеличится. Таким об% разом, ни одна из точек множества допустимs[ решений не доминируется другими, т. е. все допустимые точки оптимальны по Парето.
Максимизируем функцию z1 при условиях (10.1.5). Это легко сделать графически (рис. 10.1.1, а). Получаем:
|
1 |
|
z1* = z1max = z1(A) =7 . |
x(1) = |
4 |
, |
|
|
|
|
Переходим к максимизации функции z2 при условиях (10.1.5) и допол% нительном ограничении, позволяющем учесть, что по критерию z1 нельзя уступать более чем на δ1 . Так как z1* −δ1 =4 , то дополнительное ограниче% ние будет иметь вид
−x1 +2x2 4 . |
(10.1.6) |
109
4 |
x2 |
A |
B |
|
|
|
|
|
|
3 |
|
|
|
C |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
E |
|
D |
grad z1 |
|
|
|
x1 |
–1 |
0 |
1 |
2 |
3 |
–1 |
|
|
|
|
–2 |
|
|
|
|
4
3
2
1
–1
–1
–2
4
3
2
1
–1
–1
–2
а)
x2
grad z2 |
|
x1 |
|
|
|
|
|
0 |
1 |
2 |
3 |
б)
x2
x1
0 |
1 |
2 |
3 |
grad z3
в)
Рис. 10.1.1. Графическое решение задачи векторной оптимизации
110
