Физика / 14.________ ______ ________ ____

вакансій з концентрацією Np нам потрібно було б розглядати рух великого числа електронів по ним. Щоб усунути ці труднощі в теорії введені р- квазічастинки - ‘дірки’, за допомогою яких розглядається рух валентних електронів по вакансіям.

Діркам приписується додатній заряд, рівний по величині заряду електрона, та ефективна маса mp*, яка визначається положенням вакансій у валентній зоні. Дірки та електрони під дією зовнішнього електричного поля мають відповідні, залежні від напруженості поля E, середні швидкості направленого руху Vp та Ve. Ці швидкості, у першому наближенні, пропорційні величині напруженості поля E

Vp=upE , Ve=ueE , (1)

де коефіцієнти пропорціональності up та ue називаються рухливістю дірок та електронів відповідно. У чистому напівпровіднику дірки валентної зони та електрони зони провідності створюють власну провідність із густиною струму

j = neeVe + npeVp = neeueE + npeupE = σE (2)

де ne , ue - концентрація та рухливість електронів, а np , up - дірок.

Поклавши

σe = neeue , σp = npeup ,

власну провідність напівпровідника можна записати так

σ = σe + σp = e(neue + npup ) . (3)

Розрахунки квантової статистики для концентрацій ne електронів у зоні провідності та концентрації np дірок такі залежності від температури

У цих виразах µe та µp -хімічні потенціали електронів та дірок. При Т=0 K хімічні потенціали можна визначити через ширину забороненої ∆E зони,яка розділяє валентну зону та зону провідності

Справді, при переході електрона з валентної зони в зону провідності виникають два носії струму: електрон та дірка і на їх створення потрібна енергія рівна енергії активації ∆E. При цьому на один носій струму припадає

енергія ∆2E , що й визначає величину хімічного потенціалу. Вираз (5)

показує, що рівень Фермі EF розташований посередині забороненої зони. З підвищенням Т цей рівень трошки зміщується ближче до зони провідності

§ 85. Домішкова провідність напівпровідників

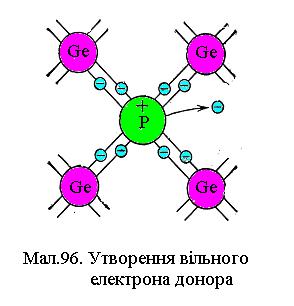
Якщо у деякі вузли кристалічної решітки чистого н/провідника помістити хімічні елементи з одним некомпенсованим зв'язком, або одним зайвим валентним електроном, то у н/провідника з'явиться домішкова провідність. Зайвий валентний електрон домішки тепловим збудженням легко відривається від атома і стає вільним носієм струму, наприклад, 5-ти валентний фосфор P у кристалі кремнію Sі. Таку домішку називають донором (див.на Мал.96).

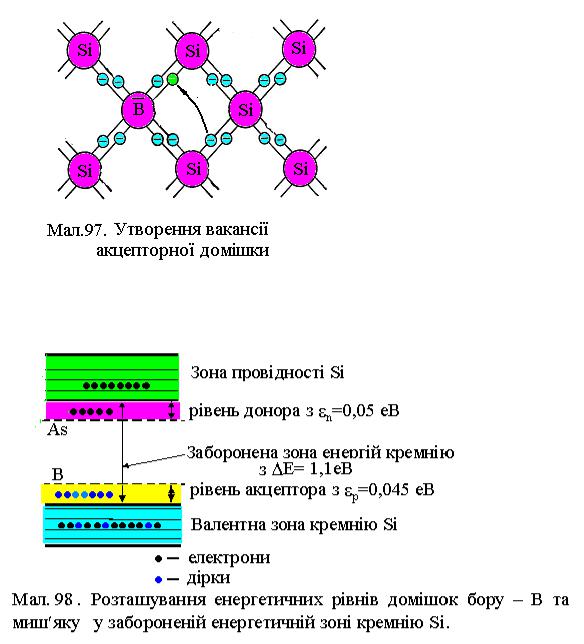
Якщо у домішки недостє електрона у зв’язку, то під дією зовнішнього електричного поля електрони основного елемента кристала

легко переміщуються по незаповненим зв’язкам (вакансіям) домішки, тобто створюють струм. Такі домішки називаються акцепторними, наприклад, домішки 3-х валентного бора (див.на Мал.97).

Для ілюстрації на на Мал.98 приведена схема розміщення енергетичних рівнів донора - As та акцептора - В у кристалі кремнію - Sі, а в Таб.2 приведені деякі характеристики кремнію та германія.

Якщо до певної температури Т0 концентрація домішок більше концентрації основних носіїв струму напівпровідника, то домішкова провідність стає основною. У цьому випадку кристали з донорною домішкою мають електронну провідність і їх називаються н/п n-типу, а акцепторні домішки дають діркову провідність і н/п називаються н/п р-типу. Для температур більше ніж деяка температура T0 концентрація основних носіїв стає більшою ніж концентрації домішок. При

цьому зникають властивості електронних приладів, набутих за рахунок

домішок.

З точки зору зонної теорії, розміщення у кристалі домішок призводить до додаткової взаємодії між атомами кристала та домішок, яка деформує основну структуру валентних та заборонених зон: з’являються донорний та акцепторний рівні енергії (див.Мал.98). Перший розташований під зоною провідності на відстані εn , а донорний над валентною зоною на відстані εp .

Добираються такі домішки, щоб εn,p були значно меншими ширини забороненої зони ∆Е

εn,p << ∆E .

Таблиця 2. Деякі характеристики кремнію та германія.

Як видно з таблиці, енергії відриву електронів донорних домішок досить малі у той же час енергія іонізації атомів цих домішок досить значна і становить для фосфору Р 10.3 еВ, для миш'яку As – 9.4 еВ, для сурьми Sb – 8.5 еВ. Це явище пояснюється впливом кристалічного поля напівпровідника на атоми донорних домішок.

§ 86. Контактні явища у металах

а). Робота виходу. Метал являє собою кристалічну решітку. При утворенні кристала атоми зближаються на такі відстані, що відбувається перекриття зовнішніх ( валентних ) та внутрішніх електронних орбіталей. При цьому перекриття валентних орбіталей настільки значне, що валентні електрони одного атома охоплюють сусідні атоми і таким чином вони сколективізуються у газ ‘вільних’ електронів: кожен із них належить усім атомам одночасно і вони можуть вільно переміщуватися в межах кристала. У вузлах кристалічної решітки розміщуються іонізовані таким чином атоми, які знаходяться у тепловому коливальному русі. Вільні електрони можуть рухатися у періодичному полі кристала під дією зовнішнього електричного поля, створюючи електричний струм. Вільні електрони мають ще назву електронів провідності. При Т> 0 К, за рахунок теплової енергії кТ (кінетична енергія), вільні електрони мають можливість виходити за поверхню кристала і повертатися у кристал за рахунок кулонівських сил тяжіння до іонів. При цьому кінетична енергія електрона переходить у потенціальну енергію кулонівської взаїмодії і навпаки.

За деякий час установлюється динамічна рівновага між кількістю електронів, що вийшли за поверхню кристала, і кількістю електронів, що повернулися у кристал. Така рівновага підтримує над поверхнею кристала електронну хмарку із середнім зарядом q− та потенціалом ϕ− (див. Мал.99).

Одночасно на поверхні кристала індукується некомпенсований додатній заряд та потенціал іонів кристалічної решітки тої ж величини, що й в електронної хмарки − q+ , ϕ+ . Таким чином над поверхнею кристала

створюється подвійний потенціальний бар’єр. Для того щоб електрон вийшов за поверхню кристала, необхідно виконати роботу проти кулонівських сил тяжіння F+, яка викликана поверхневим зарядом q+ та сили відштовхування F− , яка створюється зарядом електронної хмарки q − . Ця робота дорівнює

A = e∆ϕ, ∆ϕ = ϕ+ − ϕ− ,

де ∆ϕ − поверхнева різниця потенціалів.

б). Закони Вольта для контактної різниці потенціалів. Для сполучених провідників Вольт установив такі закони:

1. При сполученні двох провідників, виготовлених із різнорідних металів, між точками поблизу їх поверхонь (точки В і С) виникає зовнішня контактна різниця потенціалів, величина якої залежить виключно від їх хімічної природи та температури.

2. Різниця потенціалів між точками поблизу поверхонь кінців ланцюга, створеного з′єднанням різнорідних провідників, що мають однакову температуру, не залежить від хімічного складу проміжних провідників і дорівнює зовнішній контактній різниці потенціалів, що виникає при безпосередньому

з’єднанні крайніх провідників.

Першопричиною виникнення контактної різниці потенціалів є власні неоднакові роботи виходу металів. При з’єднанні таких провідників у місці контакту відбуваються переходи частини електронів із металу з меншою роботою виходу A2 у метал із більшою роботою виходу A1 (глибшою

потенціальною ямою). При цьому метал з A1 заряджається негативно, а метал з A2 - позитивно (див. Мал.100). Цей процес триває до вирівнювання роботи виходу обох металів. При цьому різниця потенціалів визначається так

Різниця потенціалів (1) називається зовнішньою контактною різницею потенціалів. Вона створюєr між вільними кінцями провідників електричне

поле напруженістю Eз .

Крім того, різні метали мають різні концентрації nі, а тому і різні енергії Фермі. При n2 > n1 електрони з другого металу дифундують у

перший. Цей процес продовжується до вирівнювання концентрацій електронів на границі контакту в обох металах. Розрахунки внутрішньої контактної різниці потенціалів за класичною теорією можна провести у такий спосіб.

При утворенні контакту двох металів з різними концентраціями вільних електронів, через їх границю починається дифузія електронів. Через деякий час концентрації електронів при границі вирівняються а метали будуть мати потенціали ϕ1,ϕ2 . З класичної точки зору концентрацію

електронів у потенціальному електричному полі з відповідним потенціалом при поверхні розділу двох металів за Больцманом можна записати у виді

Внутрішня контактна різниця потенціалів тепер запишеться так

З квантової точки зору, переміщення електронів у прошарку контакту змінює положення рівнів Фермі EF1 та EF2 в провідниках. У провідникові,

концентрацій електронів, від значення яких залежить величина енергії Фермі. Розглянутий процес спричиняє виникнення внутрішньої різниці потенціалів

а підстановка цього виразу у (3) дає

З останнього виразу видно, що внутрішня контактна різниця потенціалів залежить від температури квадратично, але залишається досить малою величиною.

Потрібно зауважити, що у зоні контакту шириною 10−10 м метали, внаслідок дифузії електронів, заряджуються різнойменно. Однак це не створює потенціального бар’єру для проходження струму у зоні контакту, як це є у напівпровіднику, тому що концентрація вільних електронів практично не змінюється.

Вираз (1) дає пояснення суті першого закону Вольта, а для пояснення другого закону розглянемо потенціали на границях металів, з'єднаних у ланцюг, як це представлено на Мал.101. Різницю потенціалів між крайніми

металами при їх поверхнях (точки В і С) можна записати у вигляді

∆ϕ17 = (ϕ1 − ϕ2 ) + (ϕ2 − ϕ3 ) + (ϕ3 − ϕ4 ) + (ϕ4 − ϕ5 ) + (ϕ5 − ϕ6 ) + (ϕ6 − ϕ7 )

і тепер ∆ϕ = ϕ1 − ϕ7 ) , що й пояснює другий закон Вольта.

§87. Термоелектрорушійна сила

У1821 році Зеебек виявив, що у замкненому колі з двох різнорідних провідників, контакти яких знаходяться при різних температурах (див. Мал.102) виникає електрорушійна сила, яку назвали термоелектрорушійною

-ТЕРС. Основними процесами, що створюють ТЕРС , є такі:

1.Дифузія електронів. В околиці контакту з більшою (меншою) температурою виникають електрони з енергіями більшими (меншими) ніж енергія Фермі. Це створює градієнт концентрації і потік гарячих електронів

унапрямку холодного контакту ( потік холодних електронів у напрямку гарячого контакту).

2.Зміна рівнів Фермі від температури. Внутрішня контактна різниця потенціалів, що визначається рівнями Фермі, різна у гарячого й холодного контактів і їх різниця, що не дорівнює нулю, як це було б при однакових температурах, дає відповідний вклад у ТЕРС.

3.Утягування електронів потоком фононів. Теплові коливання кристалічної решітки більш інтенсивні біля гарячого контакту, що створює потік фононів у напрямку холодного контакту. Останні, взаємодіючи з електронами, надають їм відповідного направленого руху. Відбувається накопичення електронів біля холодного і збіднення їх біля гарячого контакту.

Таким чином створюється стороннє силове поле не електричного походження, яке направлене назустріч градієнту температури, тобто від гарячого до холодного контакту. Такого ж роду процеси відбуваються у замкненому колі з n- та р-напівпровідників. У першому випадку напруженість силового поля направлена, як і у випадку металів, по градієнту поля, а в другому випадку - у протилежному напрямку.

Розрахунки показують, що величина термоелектрорушійної сили ε у замкненому колі визначається різницями потенціалів на контактах 1 та 2

ε = (∆ϕ1' ,2 − ∆ϕ'2,1) + (∆ϕ1'',2 − ∆ϕ'2' ,1) = (∆ϕ1'',2 − ∆ϕ'2' ,1)

і за формулою (5) можна записати

Величина α- коефіцієнт термоелектрорушійної сили, характерний для кожної з пар металів. Цей класичний результат збігається з квантово-механічним для малих різниць температур спаїв ∆T . Однак із більшенням ∆T ТЕРС перестає лінійно залежати від ∆T , а змінюється доволі складним чином аж до зміни полярності. Характерним є спай залізо-мідь. Якщо один спай підтримувати

при t = 0o C , то при температурі другого спаю при t = 540o C, ТЕРС

становиться рівною 0. При температурі меншій 540o C полярність має один знак, а при більшій – інший.

Коефіцієнт корисної дії (ККД) термопар із металів складає ~ 0.1% у той час як термопари з напівпровідників мають ККД ~ 15% і у принципі

може бути підвищеним. Проте цей ефект знайшов широке застосування у приладах, що вимірюють температуру.

§ 88. Напівпровідниковий діод

При утворенні контакту р- та n-напівпровідників через нього виникає дифузія та рекомбінація носіїв струму в обох областях. Дифузія виникає внаслідок різної концентрації електронів та дірок у сполучених р- та n-областях.

При дифузії вільного електрона з n- області там залишається додатній іон

донорної домішки Q+n (від нього саме

відірвався цей електрон) і в р-області він займає вакансію зв’язку акцепторної домішки, перетворюючи її у від’ємний іон

Q−p . Такий процес називається

рекомбінацією електрона та дірки. Слід окремо зауважити, що під час рекомбінації у контактному прошарку зникають носії струму. Під

рекомбінацією дірки у n-області слід розуміти виникнення вакансії зв'язку між атомами у ній і зайняття її електроном донора. Це означає зникнення електрона й дірки, як носіїв струму, й утворення знову ж таки додатного іона донорної домішки в n-області й від’ємного іона акцепторної домішки в p-області.

Таким чином, границя n- і р-області збіднюється носіями струму, а зарядами іонів домішок створюється внутрішнє електричне поле з