
Физика / 14.________ ______ ________ ____
.pdfВ.М.Клименко. Елементи фізики твердого тіла |
141 |
|
|
Елементи квантової статистики та фізики твердого тіла
§ 73. Статистичні методи у квантовій механіці
Як відомо, із квантової механіки, динаміку елементарних частинок, які знаходяться у силовому потенціальному полі, визначають за допомогою ψ-функцій Шредінгера. Фізичний зміст цих функцій полягає у тому, що перебування частинки у певному стані задається ймовірністю, густина якої дорівнює квадратові модуля ψ-функції. Можна ввести 6-вимірний простір із 3-х просторових координат x,y,z та 3-х проекцій імпульсу pr на них - pх,pу,pz,
який називається фазовим. Кожній точці цього простору відповідає певний
стан частинки. Імовірність стану визначається виразом |
|
dW = f (q, p ) dФ. |
( 1 ) |
У (1) через q та р умовно позначені просторові координати та проекції імпульсу відповідно, dΦ = dpdq - елемент об'єму фазового простору, а
dq = dx dy dz, dp = dpx dpy dpz .
Функція f(p,q) - густина ймовірності того, що частинка знаходиться в одиничному фазовому об'ємі з координатами q та р. Фазовий простір системи з n частинок є 6n-вимірним.
Кожна точка фазового простору повинна була б відповідати одному визначеному станові, як це є у класичній фізиці, але у квантовій механіці де координати та імпульс мають невизначеність за Гейзенбергом
dx dpx ≥ h, dy dp y ≥ h, dz dpz ≥ h |
(2) |
стану частинки відповідає деякий фазовий об'єм dФ=dqdp. Виходячи з (2) можна визначити мінімальний фазовий об'єм, що відповідає одному станові частинки
min(dq dp) = min(dx dy dz dpx dpy dpz ) = h3 .
Якщо деяка функція координат та імпульсу F(p,q) визначена на
фазовому просторі системи частинок, то її середнє |
значення < L(q,p) > |
обчислюється за правилом: |
|
< L(q,p) >= ∫ L(q,p) dW = ∫ L(q,p) f (q,p) dqdp |
(3) |
ФФ
В(3) інтегрування проводиться по усьому фазовому об'єму системи Ф.
Уведення фазового простору (q,p) та густини розподілу f(q,p) є одним із методів опису динаміки системи елементарних частинок через неперервні змінні q та p. Існують також інші методи опису динаміки стану елементарних частинок. Один із них ґрунтується на визначенні стану системи через дискретну змінну величину, якою може бути, наприклад, енергія системи. У цьому випадку функція розподілу f(q,p) визначається на множині дискретних значень енергії Еn, де n - сукупність усіх дискретних квантових
В.М.Клименко. Елементи фізики твердого тіла |
142 |
|
|
чисел, що визначають стан системи. У найбільш загальному вигляді функцію розподілу запропонував Гібсс
f(En ) = Ae |
− |
En |
|
|
|
|
|
|
|||
kT . |
|
|
|
|
(4) |
||||||
|
|
|
|
|
|||||||
Стала А визначається з умови нормування |
|
||||||||||
∞ |
− |
En |
|
|
|
|
∞ |
− |
En |
−1 |
|
kT =1, |
|
|
(5) |
||||||||
∑ Ae |
|
|
A = |
∑ e |
|
kT . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
n=0 |
|
|
|
|
|
§ 74. Розподіл Бозе-Ейнштейна та Фермі-Дірака
За типом просторової симетрії псі-функції системи квантових частинок поділяються на два види. Системи частинок, які описуються симетричними відносно перестановки координат псі-функціями, мають цілий спін і називаються бозонами, а при антисиметричних із напівцілим спіном - ферміонами. Відповідно до цього, у квантовій статистиці розглядаються дві статистики з функціями розподілу Фермі-Дірака (ферміони) та БозеЕйнштейна (бозони). Вони визначають середнє число частинок системи, що мають енергію En при температурі Т і їх можна записати у вигляді
f(En ) = |
1 |
|
, |
(6) |
||
En −µ |
|
|||||
|
e |
kT |
|
+ δ |
|
|
де δ = 1 для ферміонів, δ = −1 для бозонів. Величина µ називається хімічним потенціалом. Вона визначається величиною зміни внутрішньої енергії системи при зміні числа її частинок на одиницю. У випадку ферміонів, якими є електрони у металі, µ дорівнює енергії Фермі EF −енергії найвищого
заповненого енергетичного рівня. Для фотонів та фононів δ = −1, µ=0.
Звизначення (6) випливає, що
∑f(En ) = N,
n
де N - число частинок системи, а рівність називається умовою нормування функції розподілу f(En).
Вираз (6) можна представити у вигляді
|
|
|
µ |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
f (En ) = |
|
|
kT |
. |
||||
En |
µ |
|||||||
|
e |
kT |
+ δe |
kT |
|
|
||
При достатньо високих температурах, коли виконується нерівність
|
En |
µ |
|
|
|
|
|
||
e |
kT |
>> e |
kT |
, |
|
|
|
||
обидві статистики переходять у класичну |
|
|
|
||||||
|
|
|
−En |
µ |
|
|
|||
f(En ) = Ae |
|
kT |
, A = e |
kT |
. |
(7) |
|||
В.М.Клименко. Елементи фізики твердого тіла |
143 |
|
|
Перехід від (6) до (7) має температурну межу, що називається температурою виродження Tв системи
T = µ . |
(8) |
|
в |
k |
|
При Т < Tв система визначається однією з двох квантових статистик, а |
||
при Т > Tв - класичною статистикою (перехід від (6) до (7)). Для вільних |
||
електронів у металі середня енергія Фермі EF ≈ 2,15 еВ |
і Tв ≈ 25000 К. Це |
|
означає, що за звичайних умов електронний газ у металі потрібно розглядати як квантову систему аж до температур порядку 25000 К. Як показують розрахунки, енергія Фермі пропорційна концентрації носіїв струму у степені
2/ 3. Якщо концентрація n |
електронів у металі складає n ≈1029 м−3 , |
то у |
|||||||||
напівпровіднику |
носії струму мають |
n ≈1019 |
÷1025 м−3 . Таким чином |
||||||||
температура |
виродження |
Tвн |
для |
|
напівпровідника |
складає |
|||||
T ≈ (1025 /1029 )2 / 3 * 25000 ≈ 50 K , |
тобто |
електронний |
газ |
у |
|||||||
вн |
|
|
|
|
|
|
|
|
|
|
|
напівпровідниках завжди невироджений. |
|
|
|
|
|
||||||
§ 75. Властивості функції розподілу для металів |
|
|
|||||||||
Функція розподілу електронів у металі має вид |
|
|
|
||||||||
|
|
f (En ) = |
|
|
1 |
|
|
|
|
|
|
|
|
|
En −EF |
|
|
|
|
|
|
||
|
|
|
e |
|
kT |
+1 |
|
|
|
||
і при температурі T →0 К |
для електронів з енергією En < EF |
її величина |
|||
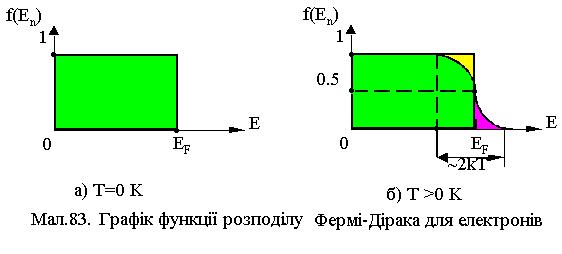
дорівнює 1 (див.Мал.83,а)). |
При температурі Т > 0 величина |
f(En) мало |
|||
змінюється в інтервалі енергій ( EF -kT, EF + kT), що |
для |
кімнатних |
|||
температур становить лише 0,025 еВ (див.Мал.83,б)). Дійсно, |
введемо заміну |
||||
змінної x = |
E n − E F |
, де х - змінна величина в одиницях kT, |
що відраховує |
||
|
|||||
|
kT |
|
|
|
|
В.М.Клименко. Елементи фізики твердого тіла |
144 |
|
|
енергію від EF , а En |
= E F + xkT . |
Тепер |
функція розподілу |
f(x) |
набуває |
||||||
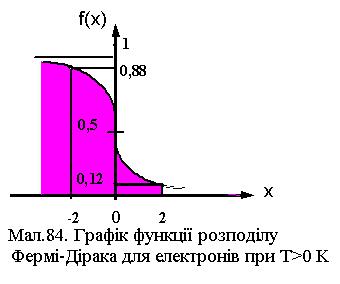
вигляду f (x) =1/(ex +1) , а таблиця значень функції буде такою |
|
||||||||||
x |
-3 |
-2,5 |
-2 |
-1 |
-0.5 |
0 |
0.5 |
1 |
2 |
2,5 |
3 |
f(x) |
0,95 |
0,92 |
0,88 |
0,73 |
0,62 |
0,5 |
0,38 |
0,27 |
0,12 |
0,08 |
0,05 |
Видно, що при зміні x від -2 до 2 значення функції розподілу Фермі - Дірака змінюється від 0,88 до 0,12. Це означає, що найбільша зміна f(E) відбувається в інтервалі енергій від EF − 2kT до
EF + 2kT . Для En = EF , f( EF ) = 0,5. Зазначимо, що величина кТ для Т=300 К має значення рівне
≈ 2.6 10−2 eB .
§ 76. Теплоємність кристалів
Розглянемо застосування квантової статистики на прикладі розгляду теплоємності твердого тіла. Класична теорія теплоємності виходить із теореми Больцмана про рівнорозподіл енергії за ступенями свободи. Згідно її положень, тверде тіло уявляється однією великою молекулою з 3N ступенями свободи, серед яких 3N-6 коливальних, 3 поступальні та 3 обертові. Так як N>>6, то можна прийняти, що усі ступені свободи є коливальними, причому кожна з них має теплову енергію kT. Повна внутрішня енергія моля такої речовини Uµ = 3NA kT =3RT . При нагріванні
кристала теплота іде на приріст внутрішньої енергії dUµ = 3RdT та на роботу по тепловому розширенню dV = V0 (1 + αdT) . Звертаючи увагу на те, що теплове розширення твердого тіла незначне ( коефіцієнт температурного
розширення α ≈10−6 ÷10−5 K-1 ), можна знехтувати роботою на розширення і вважати, що молярні теплоємності кристала при сталому тискові Сpµ та при
сталому об’ємові СVµ рівні за величиною Cpµ = Cv µ = Cµ і
|
Cµ = |
dUµ |
|
|
|
|
dT |
|
|||
|
|
|
|||
Тепер теплоємність моля твердого тіла дорівнює |
|||||
Cµ = 3R = 25 |
Дж |
|
. |
(1) |
|
моль К |
|||||
Цей результат дослідним шляхом установили Дюлонг та Пті і він |
|||||
відомий як правило Дюлонга-Пті: молярна |
теплоємність хімічно простих |
||||

В.М.Клименко. Елементи фізики твердого тіла |
145 |
|
|
речовин у кристалічному стані не залежить від температури та рівна 3R. Насправді це правило виконується лише у випадку високих температур. Для
низьких температур теплоємність твердого тіла пропорційна T3 і цей результат має лише квантово-механічне обґрунтування, тобто тверде тіло при низьких температурах необхідно розглядати як квантову систему.
Досить близькі до експерименту значення теплоємності дає теорія теплоємності хімічно простих кристалів Дебая. Його ідея полягає в тому, що найбільший внесок у теплоємність дають теплові коливання вузлів кристалічної решітки з низькими акустичними частотами ω, які мають довжини хвиль λ, більші за період d. Як і у класичній теорії вважається, що N частинок кристала мають 3N коливальних ступенів свободи. Цим ступеням свободи відповідають 3N узагальнених координат, які можна звести до 3N нормальних координат. Останні описують 3N гармонічних коливань
частинок. Такі коливання називають |
осциляторами. |
З квантової механіки |
відомо, що енергія осцилятора має дискретні значення |
|
|
En = (1/ 2 + n) hω, |
(n=0,1,2,3....). |
(2) |
По аналогії з фотонним газом, кожному з таких акустичних коливань зпівставляється квазічастинка, яку називають фононом. Вони існують лише у межах кристала. Для них виконується закон збереження енергії. Квазіімпульс фонона дорівнює
|
r |
r r |
r ω |
|
p = hk, k = n u , |
||
де kr - хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в |
|||
напрямку nr |
, ω - частота коливання осцилятора. При взаємодії фононів закон |
||
збереження імпульсу не виконується: імпульс взаємодіючих фононів може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних коливань у кристалах.
Розрахуємо число квантових станів для фононів, що мають імпульс в інтервалі від p до p+dp в об'ємі кристала V. Фазовий простір таких коливань визначається різницею об'ємів сфер імпульсу з радіусами p та р+dp і об'ємом кристала V
dΦ = 43π V [(p +dp)3 −p3 ] = 4πVp2 dp .
Як відомо, мінімальний об'єм комірки фазового простору, що
відповідає одному, певному станові системи становить h3 , тому число станів dГ в об'ємі dФ буде дорівнювати
dΓ = |
3 dΦ |
= |
3ω2dω |
V . |
(3) |
||
h3 |
2π2u3 |
|
|||||
|
|
|
|
||||
У цьому виразі коефіцієнт |
3 |
уведено з урахуванням того, що у |
|||||
кристалі можуть одночасно існувати дві поперечні хвилі (зсув кристалу) та одна повздовжня хвиля (стиснення кристалу) . З міркувань граничних умов

В.М.Клименко. Елементи фізики твердого тіла |
146 |
|
|
для стоячих хвиль, довжина акустичної хвилі λ, породженої коливаннями вузлів кристалічної решітки, не може бути меншою двох періодів кристала - 2d. Такій довжині хвилі відповідає максимальна частота коливань Ω. Повне число коливань визначається числом ступенів свободи для системи з N частинок, що рівне 3N і це дає можливість обчислити швидкість фононів u через частоту Ω
Ω 3ω2dω |
|
Ω3 |
|
|
||||
3N = ∫ dГ = ∫ |
2 |
|
3 |
V = |
|
|
|
V |
u |
2 |
u |
3 |
|||||
0 |
2π |
|
|
2π |
|
|
||
Звідси одержимо
u3 = Ω3 V 6π2 N
і після підстановки у (3), шукане число станів визнвчиться так
|
dГ = 9N |
ω2 dω |
(4) |
||||
|
|
Ω3 |
|||||
|
|
|
|
|
|
|
|
Розподіл осциляторів на можливих енергетичних рівнях (2) |
|||||||
визначається розподілом Больцмана, |
а тому середня енергія фононів < ε > |
||||||
на частоті ω обчислюється так як і у випадку фотонів (формула Планка) |
|||||||
< ε >= |
1 hω + |
|
hω |
. |
|
(5) |
|
|
|
|
|||||
|
2 |
|
hω |
|
|
|
|
|
|
|
|
|
|
|
|
|
ekT −1 |
|
|
||||
|
|
|
|
||||
Використовуючи (4-5), обчислимо внутрішню енергію Е поля фононів
кристала для моля речовини (N=NА) у такий спосіб |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
9N |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
hω |
|
|
|||||||
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Eµ = ∫ < ε > dn = |
|
|
|
|
A |
∫ |
|
|
|
|
|
hω+ |
|
|
|
|
|
ω2dω |
||||||||||||||
|
|
Ω |
3 |
2 |
|
|
|
|
hω |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e kT −1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h Ω ω3 dω |
|
|
|
|
||||||||||||||
|
|
9N |
A |
|
|
|
|
9N |
|
|
|
|
|
|||||||||||||||||||
Eµ = |
|
|
|
|
hΩ + |
|
|
|
|
A |
|
|
∫ |
|
hω |
|
|
|
|
, |
|
(6) |
||||||||||
8 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 ekT |
−1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При високих температурах, |
коли теплова енергія значно більша енергії |
|||||||||||||||||||||||||||||||
фонона kТ >> ħω, в (6) можна покласти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
hω |
|
|
|
|
|
|
|
|
hω |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
e |
|
|
|
≈ 1+ |
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|||||
При цьому інтеграл у (6) обчислюється так |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Ω |
ω3 dω |
|
|
Ω |
|
ω3 |
dω |
|
|
|
|
|
kTΩ3 |
|
|
|||||||||||||||||
∫ |
|
|
hω |
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
hω |
|
|
|
|
|
3h |
|
||||||||||||||||
|
|
|
|
|
|
|
0 1+ |
− |
1 |
|
|
|
|
|
||||||||||||||||||
0 ekT |
−1 |
|
|
|
|
|
||||||||||||||||||||||||||
kT |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В цьому наближенні одержимо
В.М.Клименко. Елементи фізики твердого тіла |
147 |
|
|
Eµ = |
9NA |
hΩ + 3NAkT |
(7) |
|
8 |
||||
|
|
|
Диференціюючи (7) по Т отримаємо теплоємність, що відповідає правилу Дюлонга-Пті
Cµ = dEdTµ = 3R .
У випадку, коли енергія фонона більша теплової енергії ħω > kT,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hω |
|
|
||
|
|
|
|
dEµ |
|
|
9N |
|
h2 Ω |
ω4e |
|
|
dω |
|
|
|||||||
Cµ = |
= |
A |
kT |
. |
(8) |
|||||||||||||||||
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|||||||||
dT |
Ω3 |
|
|
hω |
|
|
|
|||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(e kT −1)2 kT |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уведемо у (8) заміну змінної, поклавши |
|
|
||||||||||||||||||||
x |
= |
hω |
|
, θ = |
hΩ |
, xmax |
= |
hΩ |
. |
|
(9) |
|||||||||||
kT |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
kT |
|
|
||||||
Тепер інтеграл у (8) приводиться до такого вигляду |
||||||||||||||||||||||
Cµ |
|
|
|
|
T 3 |
xmax |
x 4ex dx |
. |
|
|
|
(10) |
||||||||||
= 9R |
|
|
|
∫0 |
|
(ex |
−1)2 |
|
|
|
||||||||||||
|
|
|
|
|
ϑ |
|
|
|
|
|
|
|
||||||||||
Величина ϑ носить назву характеристичної температури Дебая і визначає граничну температуру кристала, нижче якої теплоємність потрібно визначати на основі квантування
акустичного |
|
поля. |
У випадку |
||
низьких |
|
температур, |
коли |
||
T << ϑ верхня границя інтеграла |
|||||
в (10) |
xmax → ∞, а сам інтеграл |
||||
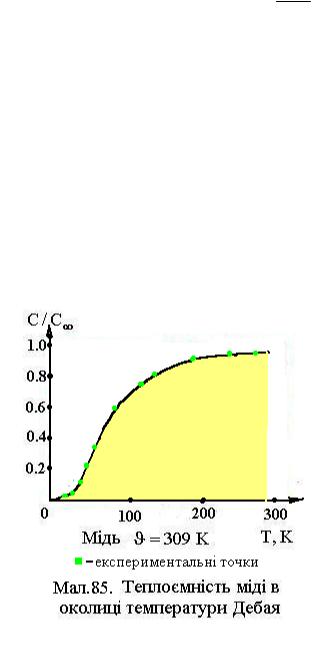
буде деяким числом. При цьому |
|||||
теплоємність |
|
буде |
пропорційна |
||
Т3, |
що |
відповідає |
даним |
||
експерименту |
|
(див.Мал.85). |
|||
Досліди показують, що одержана |
|||||
залежність |
|
теплоємності |
від |
||
температури |
|
добре |
виконується |
||
для багатьох хімічно простих речовин, а саме співвідношення відоме, як закон Дебая.
§ 77. Утворення кристалів
У процесі кристалізації (перехід речовини з рідини у тверде тіло) із розплаву чи розчину атоми речовини зближуються і між ними виникає сила

В.М.Клименко. Елементи фізики твердого тіла |
148 |
|
|
взаємодії, завдяки якій утворюється стійка кристалічна структура з певними елементами симетрії. З точки зору провідності електричного струму кристали поділяються на провідники, напівпровідники та діелектрики.
Упровідників атоми зближуються настільки, що валентні (зовнішні) електрони, рухаючись по орбітах, охоплюють сусідні атоми. При тотожності електронів (їх нерозрізнюваності), це явище робить валентні електрони cколективізованими, «вільними»:-вони можуть вільно переміщуватися у межах кристала від одного атома до іншого. Досить прикласти до провідника невелику напругу і в ньому потече електричний струм.
Унапівпровідника та діелектрика електронні оболонки валентних
(зовнішніх) електронів перекриваються між собою, не охоплюючи сусідні атоми. Таке перекриття створює силовий зв’язок між атомами, а сили взаємодії, які виникають при цьому, носять квантовий характер і називаються обмінними силами. Їх величина залежить від величини перекриття оболонок. При температурі близько 0 К валентні електрони напівпровідників та діелектриків знаходяться при атомах, а енергія, необхідна для відриву
валентного електрона від атома, становить Ea і називається енергією
активації. Ця енергія мало змінюється з температурою і практично її можна вважати сталою. У напівпровідників Ea < 5 еВ, а у діелектриків Ea ≥ 5 еВ.
Такі значення енергії Ea у напівпровідників зумовлюють можливість відриву
валентних електронів від атомів за рахунок теплової енергії kT при кімнатних температурах. У діелектриків, при таких температурах, теплової енергії, для утворення достатньої концентрації вільних електронів замало і вони практично не проводять електричний струм при напрузі меншій ніж напруга іонізації.
§ 78. Квантова теорія зонної структури кристалів
Рівняння Шредінгера у випадку періодичних граничних умов, що мають місце для руху електрона у кристалічному полі, можна представити як
− |
h2 |
|
∆ψ + Uψ = Eψ. |
(1) |
|
2m |
|||||
|
|
|
|||
В.М.Клименко. Елементи фізики твердого тіла |
149 |
|
|
У цьому виразі ψ (x,y,z) - хвильова функція, U(x,y,z) - потенційна енергія електрона у кристалічному полі, Е - енергія електрона, ∆ - оператор Лапласа
∆ = |
∂2 |
+ |
∂2 |
+ |
∂2 |
. |
|
∂x 2 |
∂y2 |
∂z2 |
|||||
|
|
|
|
Потенціальна енергія U та псі-функція ψ(x,y,z) електрона є періодичними
функціями змінних x, y, z з граничними умовами |
|
U(x+L,y,z) = U(x,y+L,z) = U(x,y,z+L) = U(x,y,z), |
|
ψ(x+L,y,z) = ψ(x,y+L,z) = ψ(x,y,z+L) = ψ(x,y,z), |
(2) |
а). Вільні електрони у періодичній просторовій структурі.
Для прикладу розглянемо кристал із кубічною симетрію, який має період решітки L. Розглянемо спочатку вільні електрони, поклавши у (1) потенціальну енергію U рівною нулю. Тепер (1) можна привести до вигляду
|
∆ψ+k2 ψ= 0 , |
|
|
k 2 |
= |
2mE |
. |
|
(3) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
r |
r |
r |
|
В (3) k - хвильове число, що задає імпульс електрона p |
= hk , де k − |
||||||||||||||||||||||||||||
хвильовий вектор. Розв'язок рівняння (3) шукаємо у вигляді |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rr |
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ(x, y, z) = Aeikr . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||
Для визначення компонент вектора k , застосуємо до (4) умови періодичності |
|||||||||||||||||||||||||||||
(2). За цих умов маємо |
|
|
eikxL |
|
= 1, |
тобто eik x L = e2iπnx , |
або |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
kx = |
2π |
nx , |
|
nx |
= 0,±1,±2,±3,... |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
ky та kz |
|
|
|
|
Аналогічно можна знайти вирази для |
|
|
|
||||||||||||||||||||||||||
|
ky = |
2π |
ny , kz |
= |
2π |
|
nz , |
|
n y,z = 0,±1,±2,±3,.... |
|
|
||||||||||||||||||
|
|
|
|
L |
|
|
|
||||||||||||||||||||||
Тепер можна записати |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
2π |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
2 |
2 |
|
|
|
||||||||
k n |
= |
|
|
|
|
|
|
n |
|
, n |
|
= (n x |
+ n y |
+ n z ) |
|
(5) |
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
З (3) визначимо енергію електрона |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2k2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
En = |
|
|
n |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|||
і, підставивши у цей вираз значення k n2 |
з (5), одержимо дискретний спектр |
||||||||||||||||||||||||||||
енергій електрона у періодичній просторовій структурі у вигляді |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h2 |
|
2π |
|
2 |
n |
2 |
|
|
|
|
|
|
|
||||||||
|
En = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, n = 0,±1,±2,.... |
(6) |
|
|
||||||||||
|
|
|
2m |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для визначення сталої А скористуємось умовою нормування |
|
||||||||||||||||||||||||||||
|
|
|
|
∫ |
|
ψ |
|
2dV = 1 |
|
|
|
|
|
|
(7) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
V
В.М.Клименко. Елементи фізики твердого тіла |
150 |
|
|
Підставимо (4) у (7) і, проінтегрувавши, одержимо
A = 1 . (8)
 L3
L3
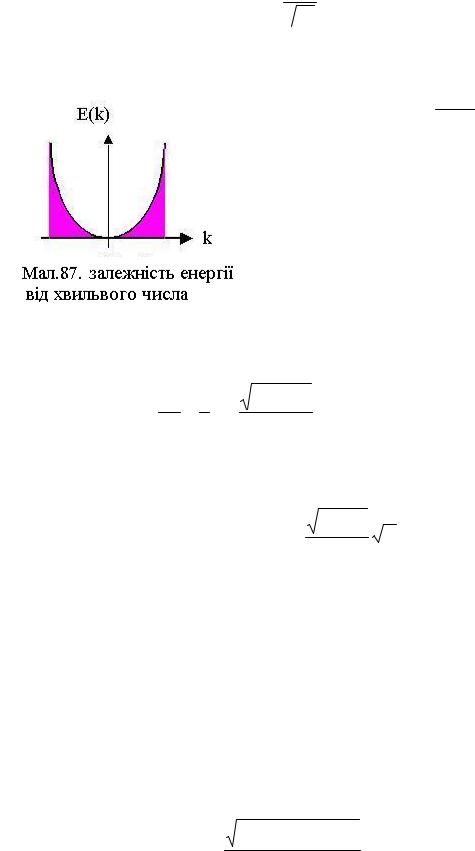
Залежність E від k має пораболічний вигляд (див.Мал.87): дискретні значення енергій En лежать на параболі
E = h2k2 . 2m
Визначимо число можливих енергетичних станів у кристалі, якщо імпульс електронів не перевищує p = hkn . Відповідний
фазовий об'єм, що припадає на такі
електрони становить |
|
|||
Φ = 2 |
4 |
πp3 |
V . |
(9) |
|
3 |
|
|
|
В (9) V- об'єм кристала, а коефіцієнт 2 враховує, що спін електрона може мати два протилежних напрямки. На один енергетичний стан приходиться
фазовий об'єм h3 , а шукане число станів
Γ = Φ |
= 8 |
πV (2mE)3 . |
(10) |
||||
e |
h3 |
3 |
|
h3 |
|
|
|
|
|
|
|
||||
Знайдемо тепер число електронів, що мають енергію від E до E+dE |
|||||||
|
dΓe = η(E) dE . |
|
(11) |
||||
В (11) множник |
|
|
|
|
|
|
|
|
|
|
η(E) = 4πV |
(2m)3 |
|||
|
|
|
h3 |
E |
|||
є густиною числа станів з енергіями Е |
|
||||||
|
|
||||||
|
|
η(E) = |
dΓe |
. |
|
(12) |
|
|
|
|
|
||||
|
|
|
|
dE |
|
|
|
Згідно принципу Паулі при температурі 0 K всі електрони розмістяться |
|||||||
по одному на кожному |
з енергетичних |
рівнів від 0 до Е. Найвищий |
|||||
заповнений енергетичний рівень енергії називається рівнем Фермі, а його енергія - енергією Фермі EF . Відповідна їй ізоенергетична поверхня у
просторі імпульсів називається поверхнею Фермі.
Вираз (10) дає можливість визначити величину енергії Фермі EF при
Т=0 К. При цій умові, число зайнятих енергетичних рівнів співпадає з числом електронів у кристалі Γe = Ne , а тому
Ne = nV = |
8 |
|
πV |
(2mEF (T = 0))3 |
, |
(13) |
|
3 |
h3 |
||||||
|
|
|
|
||||
де n - концентрація електронів.
