Физика / 12.________ _______ ______ __ _________ ________

В.М.Клименко. Елементи атомної фізики та квантової механіки 86

Елементи атомної фізики та квантової механіки.

§ 40. Борівська теорія атома водню та її обмеженість

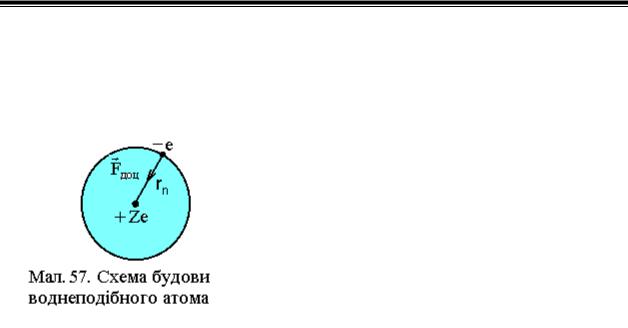
Результати дослідів по розсіюванню α −частинок на атомах дали можливість Резерфорду створити їх планетарну модель, згідно якої у центрі атома знаходиться позитивно заряджене ядро розміром ~10-15 м, а навколо нього у сфері діаметром ~10-10 м по замкнених орбітах рухаються електрони (див.Мал.57). З точки зору класичної теорії обертовий рух електрона є прискореним рухом і, як заряджена частинка, він повинен випромінювати електромагнітні хвилі суцільного спектра. При цьому повинна зменшуватися його енергія і, зрештою, він повинен упасти на ядро. Проте, усупереч цьому, атоми є стійкими утвореннями, їх спектр випромінювання є лінійним, а не суцільним.

Перша спроба побудови не класичної моделі атома, відповідно до планетарної моделі Резерфорда, була зроблена Н.Бором відносно водне подібних атомів в 1913 році. Основними положеннями якої є наступне.

1. Постулат стаціонарних станів: існують стаціонарні стани атома, знаходячись на яких, електрон не випромінює і не поглинає енергію.

2. Правило квантування орбіти: у стаціонарному стані електрон

3. Правило частот: перехід атома з одного стаціонарного стану з енергією Em у збуджений стан з більшою енергією En , cупроводжується

поглинанням енергії ∆Enm = En −Em . Перехід атома із збудженого стану в

основний супроводжується випромінюванням електромагнітної хвилі з частотою, яка визначається рівнянням

Атом поглинає електромагнітні хвилі лише коли їх частота ω задовольняє умові

Експеримент показує, що перехід електрона з одного стаціонарного стану на

інший триває коло 10−8 с.

Розрахунок орбіт та енергій воднеподібних атомів. За постулатами Бора можна розрахувати спектр енергії та радіуси стаціонарних орбіт воднеподібних атомів (атомів з одним електроном на зовнішній орбіті). З правила квантування орбіт (1) знайдемо

В.М.Клименко. Елементи атомної фізики та квантової механіки 87

n mrn

Бор вважав, що електрон у воднеподібній системі рухається по колу під дією

Підставляючи (6) у (9) одержимо вираз для енергії електрона на n-ій орбіті

В.М.Клименко. Елементи атомної фізики та квантової механіки 88

Значення величини енергії основного стану атома водню E0 і борівського радіуса орбіти основного стану rБ наведені у таблиці

швидкість електрона на першій стаціонарній орбіті атома водню. Використовуючи правило частот, можна записати

Вираз для оберненої довжини хвилі 1/ λ = ω/ 2πc випромінювання має вид

катода, прискорюються різницею потенціалів катод-сітка Uc , величина якої регулюється потенціометром R1 . Потенціометром R 2 установлюється

В.М.Клименко. Елементи атомної фізики та квантової механіки 89

різниця потенціалів Uа анод-сітка, що створює затримуюче поле для термоелектронів у просторі сітка-анод. Анодний струм I, що тече через гальванометр G виникає лише тоді, коли термоелектрони, що пройшли через сітку, мають енергію достатню, для подолання гальмівного поля. У просторі катод-сітка прискорені електрони співударяються з атомами газу. При невеликих енергіях, пружні співударяння електронів із газом змінюють лише їх імпульс і електрони, долаючи електричне поле анод-сітка, створюють анодний струм. Якщо енергія електронів досягає величини енергії збудження атомів газу ε, то співударяння носять не пружний характер, а залишкової

енергії термоелектронів недостатньо для подолання гальмівного поля сітка-анод. У цей момент анодний струм різко падає, досягаючи мінімуму.

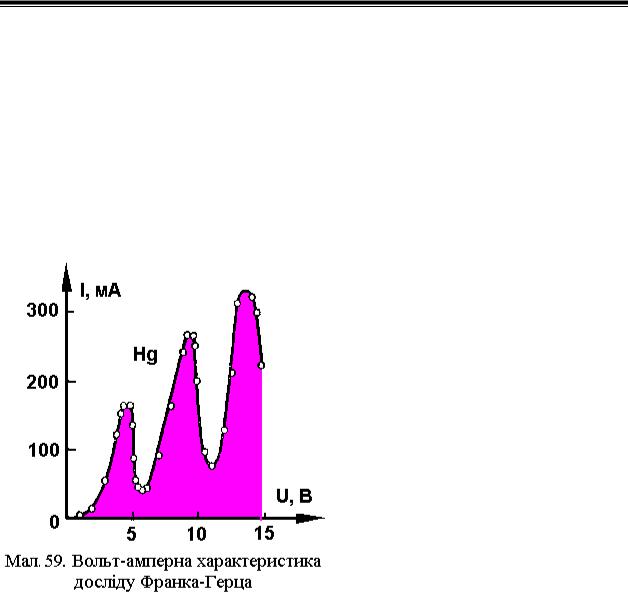
Подальше прискорення електронів знову викликає зростання анодного струму. При досягненні електронами енергій порядку 2ε, анодний струм знову різко падає до деякого мінімального значення. У випадку парів ртуті максимуми струму I спостерігалися при потенціалах U

= 4,1; 9,0; 13,9 В. (див.Мал.59.)

Різниця між цими значеннями постійна і дорівнює 4,9 В (із точністю до 0,1 В). Коли

врахувати контактну різницю потенціалів катод-сітка, що у досліді становила 0,8 В, то прискорююча напруга створювала ряд значень енергій електрона Е = 4,9; 9,8; 14,7 еВ, у якому перше значення збігається з різницею між сусідніми значеннями. Потенціал прискорення Uc1= 4,9 В називається

Таким чином, досліди Франка-Герца довелили, що енергія атомів дискретна, на що указують постулати Бора.

Обмеженість теорії Бора. Модель атома за Бором знайшла своє підтвердження в дослідах Франка-Герца при дослідженні збудження парів ртуті. Ця модель пояснила природу спектральних ліній атома водню, дозволила розрахувати його енергетичні рівні. Зоммерфельд додатково ввів поряд із сферичними еліптичні орбіти електронів. Однак теорія БораЗоммерфельда не змогла пояснити інтенсивність ліній спектра та явища

В.М.Клименко. Елементи атомної фізики та квантової механіки 90

поляризації, дисперсії та поглинання світла. Повною невдачею скінчилась спроба створити теорію атома гелію.

§ 41. Хвильова ψ-функція Луї де Бройля та її фізичний зміст

Наявність хвильових властивостей у частинок, що рухаються ставить питання про фізичний зміст їх хвильових функцій, які було названо ψ −функціями. Для характеристики хвиль де Бройля знайдемо спочатку

фазову Vф та групову Vгрп швидкості такого хвильового процесу, у якому

частинка рухається із швидкістю V<c і має енергію W. Для знаходження фазової швидкості, запишемо послідовність очевидних рівностей, що випливають з формули Луї де Бройля

тобто групова швидкість хвилі дорівнює швидкості частинки Vгрп = V .

У дослідах по дифракції електронів у різних точках простору спостерігалось більше чи менше скупчення електронів, що відповідало різним значенням інтенсивності хвиль де Бройля. Це означає наявність певної ймовірності знаходження електрона в точках простору, яка характеризується густиною ймовірності і яка зв’язана з інтенсивністю хвиль де Бройля. В 1926 р М.Борн сформулював такий фізичний зміст хвиль де

Бройля: квадрат модуля псі-функції визначає густину ймовірності dР того, що частинка знаходиться в елементі об’єму dV=dx dy dz, обмеженого координатами x, x+dx;y, y+dy; z, z+dz,

dP =| Ψ |2 dx dy dz .

За допомогою ψ-функції можна обчислити середні значення величин, які характеризують стан частинки, наприклад, для середнього значення відстані електрона від ядра можна записати вираз

< r >= ∫ Ψ r Ψ* dV .

Псі-функція повинна бути нормованою

∫ dP =∫∫∫| Ψ |2 dy dz dx =1.

V

Нормованість псі-функції означає, що ймовірність знаходження частинки в наданому їй об'ємі V дорівнює 1.

В.М.Клименко. Елементи атомної фізики та квантової механіки 91

§ 42. Рівняння Шредінгера

У класичній механіці рівняння руху за другим законом Ньютона розв’язується основна задача механіки: за заданими силами, що діють на макроскопічне тіло, та початковими умовами для координат та швидкості, знаходяться координати й швидкість тіла в будь-який момент часу. Подібним рівнянням, у квантовій механіці є хвильове рівняння Шредінгера для ψ −функції, яке він одержав в 1926 році. Це рівняння, як і рівняння руху

Ньютона, не виводиться, а постулюється. Хвильове рівняння Шредінгера

визначає хвильову функцію де Бройля Ψ(x, y,z) через потенціальну енергію силового поля U(x,y,z,t), в якому знаходиться частинка. В цьому рівнянні

оператор Лапласа. На Ψ-функцію накладаються такі умови:

а) вона має бути скінченою, однозначною та неперервною разом із своїми першою та другою похідними по x,y,z,t;

б) функція |Ψ|2, яка має фізичний зміст імовірності, має бути інтегрованою, тобто такою, що інтеграл ∫ Ψ 2 dV є скінченною величиною.

V

Записане хвильове рівняння Шредінгера, називається часовим: в ньому потенціальна енергії може залежати від часу t. Якщо потенціальна енергія не залежить від часу, то Ψ(x, y,z) −функцію можна шукати у вигляді

де Е повна енергія частинки. Дійсно, підстановка (2) у рівняння Шредінгера (1) приводить його до рівняння

яке називається стаціонарним рівнянням Шредінгера, так як воно у явному виді не залежить від t.

може перебувати, знаходячись у потенціальному полі U(x,y,z,t). Коротко зупинимось на властивостях рівняння Шредінгера

-хвильові функції повинні бути однозначними та неперервними в усьому просторі, навіть коли Потенціальна енергія буде мати поверхні розриву;

В.М.Клименко. Елементи атомної фізики та квантової механіки 92

-частинка не може проникнути у ту область, де U = ∞;

-хвильові функції повинні бути скінченими, якщо U стає нескінченною;

-хвильові функції повинні мати неперервними першу та другу похідні;

-при від'ємному значенні потенціальної енергії U енергія частинки дискретна й від'ємна, а енергетичні рівні згущуються у напрямку до рівня з Е=0.

обчислити його власне значення та відповідну власну ψ-функцію. У стаціонарному рівнянні Шредінгера можна визначити енергетичний оператор, власними значеннями якого є енергія частинки Е. Такий оператор називається оператором Гамільтона і він має вид

і розв’язати його, знайшовши Е і ψ. Узагалі для будь-якого оператора складається диференціальне рівняння

яке розв’язується при відповідних крайових умовах. Розв'язок дає власні значення q1,q2,q3...qn... та власні функції ψ1,ψ2,ψ3...ψn.... Вимірювання величини q можуть показати, що вона завжди має певне значення, а може статися, що в різних вимірюваннях будуть різні значення q. У першому випадку кажуть, що q має певне значення, а у другому випадку величина q із різною ймовірністю приймає відповідні значення зі свого спектра, а ψ - функція такого стану може бути записана у вигляді суперпозиції власних функцій

V

В.М.Клименко. Елементи атомної фізики та квантової механіки 93

Квадрат модуля ci2 визначає ймовірність того, що при вимірюванні буде одержане значення власної величини q=qі.

§ 44. Рух вільної частинки

Рух вільної частинки характеризується сталою швидкістю V, а повна енергія Е є кінетичною енергією. Направимо вісь Ох уздовж напрямку руху. Стаціонарне рівняння Шредінгера тепер матиме вигляд

де ω = E . Таким чином рух вільної частинки у квантовій механіці описується h

плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох

Ψ= Aei(ωt−kx) ,

авеличина |Ψ|2=|A|2 не залежить від часу t.

§45. Частинка у нескінченно глибокій потенціальній ямі

Нехай електрон знаходиться в одновимірній потенціальній ямі шириною L із потенціальною енергією U=0 для 0<x<L і U=∞ для (x≤0, x≥L), причому граничні умови для ψ-функції зводяться до ψ=0 при x≤0 і x≥L. Стаціонарне рівняння Шредінгера для електрона в ямі буде мати вигляд рівняння для вільного електрона

В.М.Клименко. Елементи атомної фізики та квантової механіки 94

Останній вираз означає, що на ширині ями L повинно вкладатися ціле число півхвиль де Бройля. Основним висновком із розв’язку даної задачі є те, що обмеження руху електрона у просторі призводить до виникнення

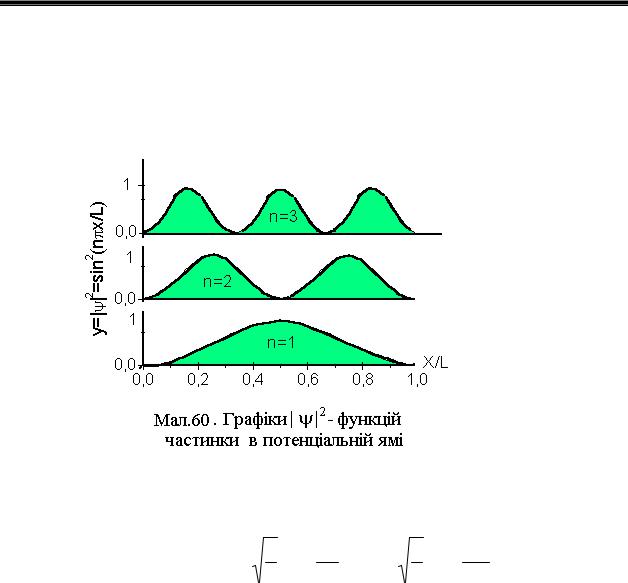
Для електрона в ямі з L=10-9 м ∆Еn=0.377 еВ, а для макроскопічної ями з L=10-2 м=1 см маємо ∆Еn=3.77 10-15 еВ і спектр енергій квазінеперервний. Розподіл імовірності знаходження частинки в ямі задається виразом

y= ψ 2 = A2 sin2 (nπLx), а максимуми її для кожного з n знаходяться в точках

В.М.Клименко. Елементи атомної фізики та квантової механіки 95

Доведемо (1) у явному виді. Підставимо у (1) значення функцій і проведемо очевидні перетворення.