
Физика / 2._________ __ _____
.pdf
В.М.Клименко. Механічні коливання та хвилі |
58 |
|
|
Коливання
§ 41. Коливальний рух
Коливальним рухом називається рух, що повторюється в часі. Якщо повторюваність відбувається за один і той же проміжок часу Т, то рух називається періодичним, а час Т періодом. За період здійснюється одне
повне коливання. Частота коливань ν = T1
одиницю часу, ω = 2πν циклічна частота. Рівняння коливання описує залежність зміщення тіла з положення рівноваги від часу.
Гармонічним називається коливання, рівняння якого описується функцією синуса або косинуса від часу кінематичне визначення, наприклад,
х = А·cos(ωt + α).
В цьому виразі х зміщення від положення рівноваги, А амплітуда коливань (максимальне зміщення), Ф(t)=ωt+α фаза коливань, Ф(t=0)=αпочаткова фаза. Якщо рух тіла спричиняється пружною силою, або квазипружною силою величина сили пропорційна зміщенню тіла зі
стану спокою), то такі коливання будуть також гармонічними. Це є динамічне визначення гармонічних коливань.
Гармонічне коливання можна представити графічно за допомогою вектора А, який обертається в площині ХОУ (див. Мал. 21). Модуль вектора дорівнює амплітуді коливання, а кут θ, який він складає з віссю ОХ дорівнює фазі коливання, тобто θ=Ф=ωt-α. Проекція вектора А на вісь ОХ здійснює коливання по гармонічному закону х=А·cos(ωt+α). Графічне зображення гармонічного коливання називається методом векторних діаграм.
В комплексній формі гармонічне коливання можна представити у вигляді:
Z = Z0eiωt ,
де Z0 = A·eiα комплексна амплітуда, модуль якої дорівнює Z0 =A, а аргумент argZ0=α. Фізичний зміст має дійсна частина комплексної величини Z, а саме x = Re Z = A cos(ωt + α) , або уявна частина
y = Im Z = Asin(ωt + α) , які представляють гармонічні коливання величин х та y відповідно.
В.М.Клименко. Механічні коливання та хвилі |
59 |
|
|
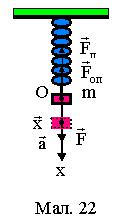
§ 42. Пружинний маятник
Пружинний маятник являє собою тіло, підвішене на пружині, масою
якої, порівнюючи з масою тіла m, можна знехтувати (див.Мал. 22). Створимо |
||||
r |
|
|
|
|
зовнішньою силою rF зміщення маятника зі стану рівноваги |
||||
xr. Напрямок сили F буде співпадати з напрямком |
||||
прискорення маятника |
d 2 xr |
. У протилежному напрямку |
||
dt |
2 |
|
||
|
|
|
||
|
r |
r |
||
будуть діяти пружна сила Fп та сила опору Fоп. Величина |
||||
пружної сили Fп = kx, де х величина зміщення тіла зі |
|
||||||
стану рівноваги, k жорсткість пружини, а сила опору |
|||||||
|
r |
|
r |
|
|
|
|
|
|
= −ζdx |
, де ζ −коефіцієнт опору. Лінійна |
|
|||
дорівнює F |
|
|
|||||
|
оп |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
залежність пружної сили від зміщення виконується лише |
|||||||
для малих коливань. |
|
|
|
|
|
|
|
Рівняння другого закону Ньютона для тіла тепер має вигляд |
|
|
|||||
m |
d2xr |
|
r r |
r |
(1) |
|
|
|
= F + F + F . |
|
|
||||
|
dt2 |
|
п |
оп |
|
|
|
r r r |
|
|
|
|
2 r |
|
|
|
|
|
|
|
, |
||
Усі сили F, Fп, Fоп, що діють на тіло й вектор прискорення ar = d |
x |
||||||
|
|
|
|
|
dt2 |
|
|
лежать на одній прямій, а тому, взявши напрямок прискорення за додатній, через прості перетворення, запишемо рівняння (1) в алгебраїчній формі
m |
d2x |
= F − F |
− F . |
(2) |
|
dt2 |
п |
оп |
|
|
|
|
|
Підставимо в (2) значення сил і запишемо його запишемо у канонічній формі
|
|
|
|
d2x |
+ 2γ |
dx |
2 |
(3) |
||
|
|
|
|
dt2 |
dt |
+ ω0 x = f , |
||||
|
F |
|
k |
|
|
|
|
|||
де f = |
, ω02 = |
, ω0 власна частота, яку називають частотою вільних |
||||||||
|
m |
|||||||||
|
m |
|
|
ζ |
|
|
|
|||
незгасаючих коливань, γ = |
коефіцієнт згасання коливань. Період |
|||||||||
2m |
||||||||||
|
|
|
|
|
|
|
|
|
||
вільних незгасаючих коливань |
|
|
|
|||||||
m
∫ dT = c 2 ∫ dm .
m 0
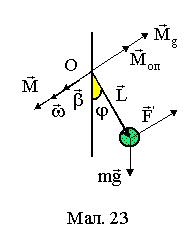
§ 43. Математичний маятник
Математичний маятник точкове тіло маси m, підвішене на нерозтяжному підвісі L, розмірами якого , порівнюючи з довжиною підвісу,
В.М.Клименко. Механічні коливання та хвилі |
60 |
|
|
можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання |
r |
описуються кутом відхилення тіла від положення рівноваги ϕ. Вектор L |
|
задає точку прикладання сил. Коливання здійснюються в загальному випадку |
||||||||||||||
|
|
|
r |
rr |
|
|
r |
|
|
|
|
|
|
|
під дією моменту M =[rF] зовнішніх сил F, моменту сили тяжіння |
||||||||||||||
r |
r |
|
r |
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
dϕ |
, де ζ коефіцієнт опору. |
|||||||
Mg =[L |
mg] та моменту сил опору Mоп = −ζ |
|
|
|
||||||||||
|
dt |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
r r |
r |
|
||
|
|
|
|
Вектори моментів сил M, Mg |
, Mоп та кутового |
|||||||||
|
|
|
|
|
|
|
r |
d2 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
ϕ |
лежать на осі обертання, яка |
||||||
|
|
|
|
прискорення β = |
dt |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
площині коливання та проходить через центр |
||||||||||
|
|
|
|
обертання О. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Величину моменту сили тяжіння можна |
||||||||
|
|
|
|
записати у вигляді Mg = mgLsin ϕ. Для малих |
||||||||||
|
|
|
|
коливань ϕ маємо sinϕ ≈ ϕ і Mg = mgLϕ. За другим |
||||||||||
|
|
|
|
законом Ньютона для обертового руху маятника |
||||||||||
|
|
|
|
рівняння коливань можна записати так |
||||||||||
|
|
|
|
|
d2 |
r |
r r |
|
|
r |
|
|
|
|
|
|
|
|
J |
ϕ |
|
|
|
|
|
|
|||
|
|
|
|
dt |
2 |
= M + Mg |
+ Mоп , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
r |
r |
r r r |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
де J=mL |
2 |
|
|
|
|
|
|
|
|
|
d2ϕ |
|||
|
момент інерції точкового тіла. Вектори β = |
dt2 |
,M,Mg ,Mоп |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній , векторне рівняння можна записати в алгебраїчній формі
|
|
|
J |
d2 |
ϕ |
+ ζ |
dϕ |
+ mgLϕ= M . |
|
|
|
|||
|
|
|
dt |
2 |
dt |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
В канонічному вигляді це рівняння має вигляд: |
|
|
|
|||||||||||
|
|
|
d 2 ϕ |
|
+ 2γ |
dϕ |
|
+ ω02 ϕ = M / J , |
|
|
|
|||
|
|
|
dt 2 |
dt |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
де γ = |
ζ |
коефіцієнт згасання коливань, ω02 = mgL |
= |
g |
, ω0 частота |
|||||||||
2J |
L |
|||||||||||||
|
|
|
|
|
|
|
|
|
J |
|
|
|||
вільних незгасаючих коливань, або частота власних коливань маятника.
§ 44. Фізичний маятник
Фізичний маятник макроскопічне тіло, що здійснює малі періодичні коливання.rВісь обертання маятника О зміщена відносно центра мас тіла Oc
на вектор L . Коливання визначаються кутом ϕ відхилення тіла від положення рівновагиr r. Ці коливання здійснюютьсяr в загальному випадкуr r під
дією моменту M =[rrF] зовнішніх сил F, моменту сили тяжіння Mg =[L mgr]

В.М.Клименко. Механічні коливання та хвилі |
61 |
|
|
та моменту сил опору Mr оп = −ζ dϕr , де ζ коефіцієнт опору. Величину dt
моменту сили тяжіння можна записати у вигляді: Мg = mgLsinϕ. Для малих коливань маятника маємо sinϕ ≈ ϕ і Мg = mgLϕ.
|
Mоп |
Mg |
|
O |
|
M |
ϕ L |
F |
ω,β |
Oc |
|
mg
Мал. 24
в алгебраїчній формі:
Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна
записати такr: |
|
|
|
||||||
|
|
|
J |
d2 |
ϕ |
|
r r |
r |
(1) |
|
|
|
dt |
2 |
= M + Mg + Mоп , |
||||
де J rмомент інерції тіла. Вектори |
|
||||||||
r |
d2 |
ϕ |
|
r |
|
r |
r |
лежать на одній прямій, а |
|
β = |
dt |
2 |
, M, Mg , Mоп |
||||||
|
|
|
|
|
|
|
|
||
тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати
|
|
J |
d 2 |
ϕ |
+ ζ |
dϕ |
+ mgL sin ϕ = M . |
|
(2) |
||||||||
|
|
dt |
2 |
|
dt |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В канонічному вигляді рівняння (2) можна записати так |
|||||||||||||||||
|
|
|
d 2 ϕ |
+ 2γ |
dϕ |
+ ω02 ϕ = M / J , |
|
(3) |
|||||||||
|
|
|
dt 2 |
|
|
||||||||||||
|
ζ |
|
|
|
|
dt |
|
|
mgL |
|
|
||||||
де γ = |
коефіцієнт згасання коливань, ω02 = |
, ω0 |
частота вільних |
||||||||||||||
2J |
J |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
незгасаючих коливань. Період малих власних коливань маятника T0 = 2π/ω0 і |
|||||||||||||||||
T0 = 2πE=T+, де lпр = lпр = |
|
J |
приведена |
)* |
довжина фізичного маятника. |
||||||||||||
Lm |
|
|
|||||||||||||||
§ 45. Крутильний маятник
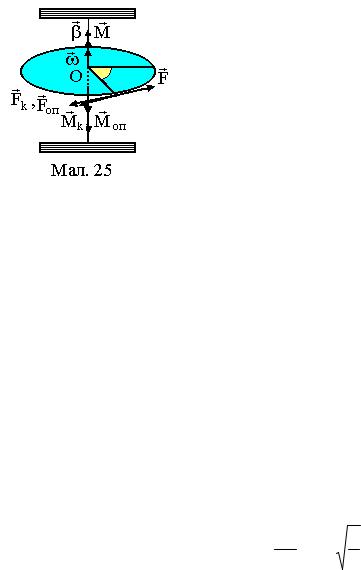
Крутильний маятник макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні. Коливання визначаються кутом
відхилення ϕ тіла від положення рівноваги, вектором кутової швидкості dϕr dt
та вектором кутового прискорення βr = d2ϕr . Тіло здійснює малі періодичні dt2
)* Приведена довжина фізичного маятника є довжина підвісу математичного
маятника з періодом рівним періоду коливань фізичного маятника.
|
|
|
|
|
В.М.Клименко. Механічні коливання та хвилі |
62 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
rr |
|
|
r |
|
||||
коливання під дією моменту M |
=[rF] зовнішньої сили F, моменту |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
r |
r |
r |
||
|
|
|
|
|
|
|
|
|
= −ζ |
dϕ |
|
|||||||||||||
|
|
|
|
|
|
|
|
Mоп |
|
dt |
сили опору Fоп |
та моменту Mk |
= −fϕ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
||||
|
|
|
|
|
|
|
|
пружної сили деформації кручення Fk . Кефіцієнт f |
||||||||||||||||
|
|
|
|
|
|
|
|
називається модулем кручення. Лінійна залежність |
||||||||||||||||
|
|
|
|
|
|
|
|
моменту сил кручення від кута повороту |
|
|||||||||||||||
|
|
|
|
|
|
|
|
виконується лише для малих коливань. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
За другим законом Ньютона для обертового |
||||||||||||
|
|
|
|
|
|
|
|
руху, рівняння коливань маятника можна записати |
||||||||||||||||
|
|
|
|
|
|
|
|
так:r |
|
|
|
r |
|
|
|
r |
r |
|
|
|||||
|
|
|
|
|
|
|
|
J |
d2 |
ϕ |
|
|
|
|
|
|
(1) |
|
||||||
|
|
|
|
|
|
|
|
dt |
2 |
|
= M |
|
+ Mk + Mоп . |
|
||||||||||
|
|
r |
d2 |
r |
r r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ϕ |
|
|
|
лежать на одній прямій, а тому, взявши |
|
|||||||||||||||||
Вектори β = |
dt |
2 |
, M, Mk , Mоп |
|
|
|||||||||||||||||||
напрямок кутового прискорення βr |
|
|
за додатній, векторне рівняння (1) можна |
|||||||||||||||||||||
записати в алгебраїчній формі: |
|
d2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
J |
ϕ |
= M − Mk − Mоп, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
2 |
|
|
|
|||||||
і в канонічному вигляді: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
J |
d2 |
ϕ |
+ 2γ |
dϕ |
|
|
|
|
|
2 |
ϕ= M / J , |
(2) |
|
||||||
|
|
|
|
|
dt |
2 |
dt |
|
+ ω0 |
|
||||||||||||||
|
ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02 = f , ω0 |
|
|
||||||
де γ = |
коефіцієнт згасання коливань, |
частота вільних |
||||||||||||||||||||||
|
||||||||||||||||||||||||
|
2J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
||
незгасаючих коливань. Період малих власних коливань маятника |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
= |
|
2π = 2π |
J . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
ω0 |
f |
|
|
||||
§ 46. Електричний коливальний контур
Коливальним RLC-контуром називається замкнене електричне коло, в якому є конденсатор із ємністю С, омічний опір R та соленоїд з індуктивністю L. В це коло може бути ввімкнено джерело струму зі змушучою електрорушійною силою Е = Е0cosωt. Протікання струму І в контурі створює на елементах контуру напругу: на опорі UR = IR , на
конденсаторі UC = q / C та електрорушійну силу індукції у соленоїді
Ei = −L dIdt .

В.М.Клименко. Механічні коливання та хвилі |
63 |
|
|
За законом збереження енергії робота джерела струму по перенесенню одиничного заряду UR + UC виконується за рахунок енергії джерела струму E + Eі, і тоді UR+UC=E+Eі.
Підставляючи відповідні вирази для напруги |
|||
та електрорушійних сил, одержимо: |
|||
IR + E= = E0cosωt - L |
dI |
. |
|
|
|||
00 |
|
dt |
|
Зважаючи на те, що I = dq |
, зведемо |
||
dt |
|
|
|
одержане рівняння до неоднорідного |
|||
диференціального рівняння коливань в |
|||
канонічному вигляді: |
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
d2q |
+ 2γ |
dq |
2 |
|
|
|
|
|
|
|
|
|
|
|
dt |
2 |
dt |
+ ω0q = e0 cosωt , |
||
|
|
R |
|
1 |
|
|
Eo |
|
|
|
|
|
|||
де γ = |
|
, ω02 = |
, e0 = |
. |
|
|
|
|
|
|
|
||||
|
|
LC |
L |
|
|
|
|
|
|
|
|||||
|
|
2L |
|
|
|
|
|
|
|
|
|
|
|||
|
Якщо продиференціювати рівняння для заряду, одержимо канонічне |
||||||||||||||
диференціальне рівняння коливань для струму |
|
|
|||||||||||||
|
|
|
|
|
J |
d2I |
+ 2γ |
dI |
|
2 |
= −ωe |
0 sin ωt . |
|||
|
|
|
|
|
dt2 |
dt |
+ ω0 I |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
§ 47. Вільні незгасаючі коливання
Якщо знехтувати силами опору (γ=0) при відсутності зовнішних сил, то рівняння вільних згасаючих коливань перетвориться в рівняння вільних незгасаючих коливань:
|
d2ϕ |
+ ω02 |
ϕ = 0. |
(1) |
|
|
|||
|
dt2 |
|
|
|
Його розв'язок представляє гармонічні коливання і матиме вигляд: |
||||
ϕ(t) = а0cos(ω0t+α). |
(2) |
|
|
|
В (2) a0 −амплітуда коливань - максимальне відхилення тіла з
положення рівноваги. Амплітуда є додатною величиною. В (2) косинус є періодичню величиною з періодом 2π і періодом T, тому
cos(ω0 t + α) = cos[ω0 (t + T) + α] = cos(ω0 t + ω0T + α) . |
(3) |
В (3)
ω0T = 2πi T = 2π/ ω0 .
Приклад. Знайти період власних коливань системи тіл, що складається зі стержня маси М=1 кг довжиною L=1 м та двох куль масами m1=1 кг та m2=4 кг, що знаходяться на кінцях стержня відносно осі. Вісь коливання

В.М.Клименко. Механічні коливання та хвилі |
64 |
|
|
проходить перпендикулярно стержню через точку, віддалену від центра стержня на відстань а=0.1 м.
Розв'язок 1). Знайдемо за визначенням центр мас
системи, розглянувши стержень, як точкове тіло маси М, що знаходиться посередині стержня. Виберемо точкою відліку точку А та проведемо через неї
вісь ОХ вздовж осі стержня. Координата центра мас системи за визначенням запишеться у вигляді
Xc = |
m1 0 +M L / 2 +m2 L |
= |
1 0.5 + 4 1 |
= |
4,5 |
= 0,75 м |
||
|
|
1+1+ 4 |
|
6 |
||||
|
m1 +M +m2 |
|
|
|
||||
Відстань від центра мас системи до осі коливання l=Xc-(L/2+a)=0.75-0.60=0.15.
Момент інерції системи стержень+дві кульки відносно осі коливання
J = (ML2 /12 +Ma2) +[m (L / 2 + a)2 ] +[m (L / 2 − a)2 ] =1,093 кг м2 |
||||
1 |
|
|
2 |
|
Період коливання фізичного маятника |
|
|
||
T = 2π |
J |
= 2π |
1,093333 |
= 2,21c |
|
mgl |
|
6 9,8 0,15 |
|
§ 48. Вільні згасаючі коливання
Коливання, що відбуваються у відсутність зовнішніх сил F, називаються вільними. Якщо при цьому існують сили опору, коливання будуть вільними згасаючими.
Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору
J |
d2 |
ϕ |
+ 2γ |
dϕ |
|
2 |
ϕ= 0 . |
(1) |
|||
dt |
2 |
dt |
+ ω0 |
||||||||
Розв'язок (1) шукаємо підстановкою Ейлера ϕ=eλt. Знайдемо перші дві |
|||||||||||
похідні від ϕ по часу |
|
|
|
|
|
d2ϕ |
|
|
|
|
|
dϕ |
|
λt |
|
|
= |
2 λt |
|
|
|||
|
|
= λe |
, |
|
λ e |
. |
(2) |
||||
|
dt |
dt2 |
|||||||||
Підставляючи похідні (2) в (1), одержимо: |
|
|
|||||||||
eλt ( λ2 + 2γλ + ω02 ) = 0. |
(3) |
||||||||||
Квадратне рівняння λ2 + 2γλ + ω02 = 0 в (3) називається характеристичним. Його розв'язок
λ1 = −γ + γ2 − ω02 , λ2 = −γ − γ2 − ω02 |
(4) |
В.М.Клименко. Механічні коливання та хвилі |
65 |
|
|
дає два фундаментальні розв'язки диференціального рівняння
ϕ1 = exp(λ1t), ϕ2 = exp(λ2t), |
(5) |
з яких утворюється загальний розв'язок. Загальним розв'язком однорідного рівняння (1) буде лінійна комбінація фундаментальних розв'язків
ϕ = Аexp(λ1t) + Bexp(λ2t) |
(6) |
з дійсними коефіцієнтами А, В. |
|
Можливі два випадки руху маятника: |
|
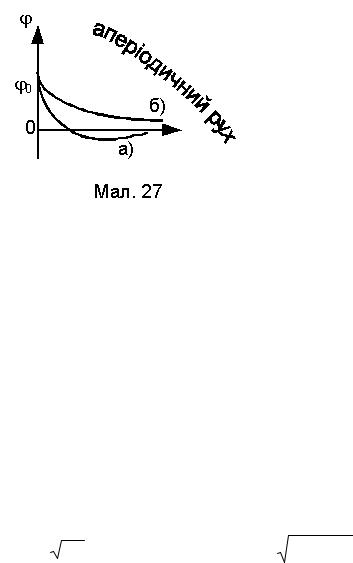
1) При γ > ω0 аперіодичний рух. При цьому λ1,λ2 < 0 дійсні числа. Функція ϕ є спадною функцією часу (λ1,λ2<0) і описує асимптотичне, експоненціальної залежності від часу, повернення маятника в стан рівноваги. При цьому коливальний рух не здійснюється. Якщо за початкових умов (у
момент часу t = 0), |
початкове зміщення |
||||
ϕ(0) = ϕ0, а початкова швидкість |
dϕ |
t=0 = |
|||
dt |
|||||
V0, то два рівняння |
|
|
|
||
|
|
|
|
||
ϕ0 = А + В; V0 = Aλ1 + Bλ2 |
(7) |
|
|
|
|
мають розв'язком |
|
|
|
|
|
А = (λ2 ϕ0 - V0)/(λ2 - λ1), B = ( λ1 ϕ0 - V0)/(λ1 - λ2). |
(8) |
|
|||
Залежно від початкових умов, можливі два випадки аперіодичного повернення маятника до стану рівноваги (див. Малюнок 27). При ϕ0 > 0 i V0 < 0 із V0 < λ1ϕ0 коефіцієнт B буде менше нуля, а з ним
ϕ = Аexp(λ1t) + Bexp(λ2t) < 0 |
(9) |
повернення (див. Малюнок 27) має тип а), тобто можливе проміжне відхилення маятника зі стану рівноваги в протилежному напрямкові, а в усіх інших випадках тип б) безпосереднє повернення до стану рівноваги.
2) Якщо γ < ω0, маятник буде здійснюватиколивальний рух. При цьому
λ1 = - γ+іω, λ1 = - γ+іω, |
(10) |
де і = −1 уявна одиниця, ω = ω02 − γ2 |
частота вільних згасаючих |
коливань. Загальний розв'язок буде мати вигляд: |
|
ϕ = e-γt(Aeiωt + Be-iωt) |
(11) |
з комплексними коефіцієнтами А, В. Для знаходження величин А та В зауважимо, що функція ϕ є дійсною функцією часу, і за цим вона має дорівнювати своїй комплексно спряженій функції ϕ = ϕ*
e-γt(Aeiωt+Be-iωt) = e-γt(A*e-iωt +B*eiωt). |
(12) |
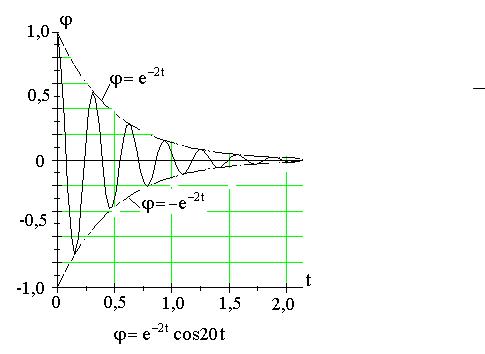
В.М.Клименко. Механічні коливання та хвилі |
66 |
|
|
Прирівнюючи в (12) коефіцієнти при однакових експонентах, одержимо В=А*. Для зручності комплексну сталу А візьмемо в
експоненціальному вигляді А = а0eiα/2, де а0 дійсна величина. Тепер
ϕ = а0/2·e-γt (ei(ωt+α) +e-i(ωt+α)) (13)
і, користуючись формулою Ейлера e±ix = cosx ± i sinx, вираз в дужках запишемо у вигляді:
ϕ = 21 а0e-γt
[cos(ωt+α)+i sin(ωt+α)+cos(ωt+α)- i sin(ωt+α)]
ϕ = ϕ0(t) cos(ωt+α). |
(14) |
В (14) ϕ0(t) = a0e-γt |
|
амплітуда коливань спадна функція часу, Ф = ωt+α фаза коливань, Ф0 = α початкова фаза.
На малюнку представлена залежність кута відхилення ϕ фізичного маятника при вільних
згасаючих коливаннях з сталою згасання γ = 2 іω= 20.
§ 49. Характеристики вільних згасаючих коливань
Вільні згасаючі коливання мають своїми характеристиками
•час релаксації,
•кількість повних коливань за час релаксації.
•декремент згасання,
•логарифмічний декремент згасання,
•добротність коливальної системи,
Час релаксації τ це час, за який амплітуда коливання зменшується в е
раз
ϕo(t) = Aexp(-βt)
e = ϕo(t) / ϕo(t+τ)= exp(βτ)
τ = 1/β. |
(1) |
За час релаксації система здійснить Ne=τ/T=1/(γT) повних коливань.
Декремент згасання за визначенням є відношення амплітуд через період
В.М.Клименко. Механічні коливання та хвилі |
67 |
|
|
d = |
ϕ(t) |
= |
a 0 e−γt |
= e γT , |
|
ϕ(t + T) |
a 0 e−γ(t+T) |
||||
|
|
|
|||
а логарифмічний декремент згасання за визначенням є |
|||||
|
ln d = ln eγT = γT |
|
|||
і в іншому виді ln d =1/ Ne .
Енергію коливальної системи можна знайти на прикладі пружинного маятника масою m із сталою пружності k. Нехай його згасаючі коливання описуються функцією
x = x 0 (t) cos(ω0 t − α) ,
де x |
0 |
(t) = a |
0 |
e−γt , ω2 = k / m . Повна енергія маятника в кожний момент часу |
|||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
визначається амплітудою |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
E = |
kx 02 (t) |
, |
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
зокрема, для t = 0 |
E = |
ka 02 |
. В довільний час t потенціальна енергія |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Eп = |
|
kx 2 |
(t) , |
|
|
|||||||
а кінетична енергія |
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dx 2 |
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
E = |
|
mV |
|
(t) = E = |
|
|
m |
|
. |
|||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||||
|
|
У випадку фізичного маятника потрібно в одержаних результатах |
|||||||||||||||||||
замінити х0(t) на ϕo(t), а масу маятника m на момент інерції J. Добротність коливальної системи за визначенням є
Q = 2πE(t) , Aт
де E(t) енергія системи в час t, AT = E(t) − E(t + T) робота системи
проти сил опору за період Т. Прийнявши до уваги, що енергія пропорційна квадрату амплітуди, можемо записати вираз для добротності у вигляді:
Q = 2π |
ϕ2 |
(t) |
|
|
|
|
|
|
||
ϕ2 (t) − ϕ2 (t + T) |
|
|
||||||||
Q = 2π |
|
|
e−2γt |
|
= |
|
2π |
|
. |
|
e−2 |
γt − e−2γ(t |
+T) |
|
− e−2 |
γT |
|||||
|
1 |
|
||||||||
Для малих сил опору γ<<1 і з достатньою точністю можна записати: e−2γT 1 − 2γT .
Тепер добротність коливальної системи з незначними силами опору можна записати у такий спосіб:
