Kurs_vysshei_matematiki_UP_Berkov_N.A._2007-2
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
Н.А. Берков, А.И. Мартыненко,
В.Б. Миносцев, Е.А. Пушкарь, О.Е. Шишанин
КУРС ВЫСШЕЙ МАТЕМАТИКИ
Под редакцией В.Б. Миносцева
Часть III
8-е издание, стереотипное
Рекомендовано Министерством образования Российской Федерации
в качестве учебного пособия для студентов
высших учебных заведений
Москва 2007
УДК 517
ББК 22.1я73 К93
Рецензент
У.Г. Пирумов, чл.-корр. РАН, проф. засл. деятель науки РФ.
Курс высшей математики. Часть III: Учебное пособие. / Н.А. Берков, К93 А.И. Мартыненко, В.Б. Миносцев, Е.А. Пушкарь, О.Е. Шишанин;
Под ред. засл. раб. ВШ РФ д.ф.-м.н., проф. В.Б. Миносцева. – 8-е изд., стереотип. – М.: МГИУ, 2007. – 489 с., 78 ил., библиогр. спис. 19
наим.
ISBN 978-5-2760-1532-3 (Ч.3)
ISBN 978-5-2760-0947-6
Учебное пособие предназначено для студентов высших технических
учебных заведений и соответствует государственному образовательному стандарту.
Пособие включает в себя лекции и практические занятия. Третья часть пособия содержит 34 лекции и 34 практических занятия по следующим разделам: дифференциальные уравнения в частных производных, элементы вариационного исчисления и теории оптимизации, теория вероятностей и математическая статистика.
УДК 517
ББК 22.1я73
|
Н.А. Берков, А.И. Мартыненко, |
|
В.Б. Миносцев, Е.А. Пушкарь, |
ISBN 978-5-2760-1532-3 (Ч.3) |
О.Е. Шишанин, 2000, 2002 |
ISBN 978-5-2760-0947-6 |
МГИУ, 2000, 2002 |
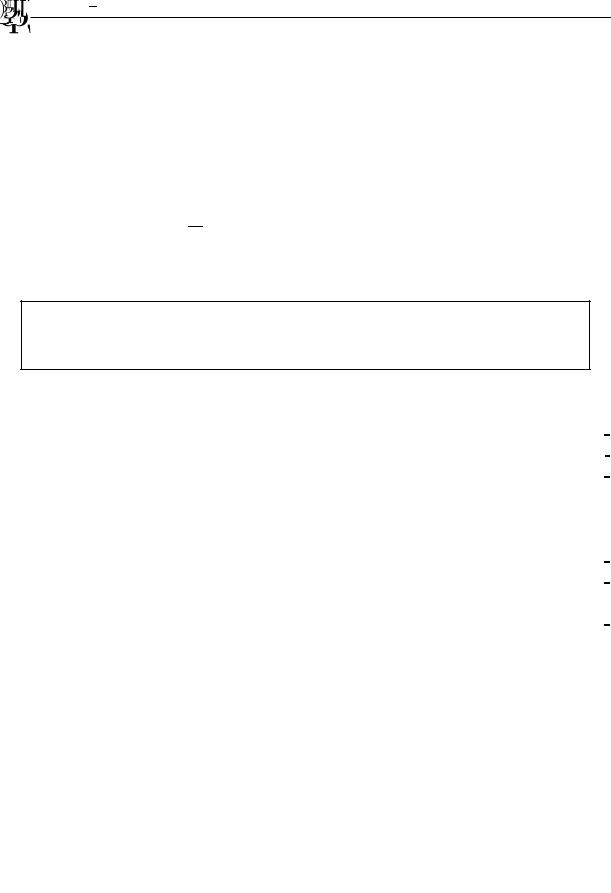
z |
∂U |
|
+ y |
∂U |
= 0; |
|
y |
∂z |
+ x |
∂z |
= (x − y)z; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∂x |
∂y |
|
∂x |
∂y |
||||||||||||||||||||||
|
|
|
|
xz |
∂U |
= yU 2; |
|
|
z |
∂z |
− x |
∂z |
|
= z; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
∂x |
|
|
∂x |
∂y |
|||||||||||||||||||
|
|
∂U ∂U |
|
|
|
|
∂z |
2 |
|
|
∂z |
|
|
∂z |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
= yz; |
|
|
− |
|
|
· |
|
|
= x2; |
|||||||||||
|
|
∂x ∂y |
∂x |
∂x |
∂y |
|||||||||||||||||||||
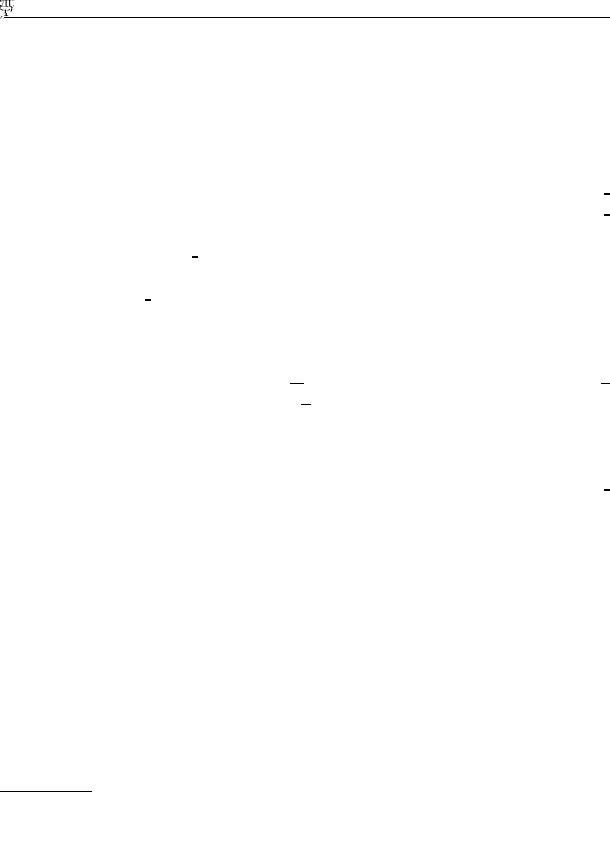
|
∂2U |
+ |
∂U |
|
3 |
|
|
|
∂z |
|
2 ∂2z |
|
|
∂z ∂2z |
= z2; |
|
|||||||||||
|
|
|
|
|
|
|
= 0; |
|
|
|
+ |
|
|
|
|
|
|
||||||||||
|
∂x∂z |
∂y |
|
∂x |
|
∂x2 |
∂x ∂y2 |
|
|||||||||||||||||||
∂U |
∂3U |
|
|
|
|
∂U |
|
2 |
|
|
|
∂3z |
|
|
|
∂z |
|
∂z |
|
2 |
|||||||
|
|
|
|
|
= z3; |
|
|
|
|
|
|
= 0. |
|||||||||||||||
|
· |
|
− |
|
|
|
|
|
− |
|
− |
|
|||||||||||||||
∂x |
∂y∂z2 |
∂x |
|
|
|
∂x2∂y |
∂y |
∂x |
|||||||||||||||||||
|
U |
x y z U = U (x, y, z) |
|
z |
x |
y  z = z(x, y)
z = z(x, y)













 U
U
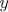




 z = (x2 + y2)1/2
z = (x2 + y2)1/2
|
|
|
|
∂2z |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∂x∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2z |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x∂y |
|||
∂z |
= |
|
|
|
x |
|
|
|
|
|
|
|
|
∂2z |
= − |
|
xy |
||||
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
∂x |
|
(x2 + y2)1/2 |
|
|
|
|
∂x∂y |
(x2 + y2)3/2 |
|||||||||||||
|
|
f U, |
∂U |
, |
∂U |
, |
|
∂U |
, |
∂2U |
, · · · |
|
|
|
|
|
|
||||
|
|
|
∂x |
∂y |
|
∂z |
∂x2 |
|
|
|
|
|
|
||||||||
f U, |
U |
|
∂U ∂U ∂2U |
, · · · = a1(x, y, z) · U + a2(x, y, z) · |
|
|
|
|
|||||
|
∂U |
|
∂U |
+ a3(x, y, z) · |
∂U |
+ · · · , |
|||||||
|
|
, |
|
, |
|
, |
|
|
|
||||
|
∂x |
∂y |
∂z |
∂x2 |
∂x |
∂y |
|||||||
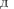





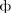






 ai(x, y, z)
ai(x, y, z) 










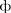
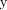









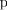










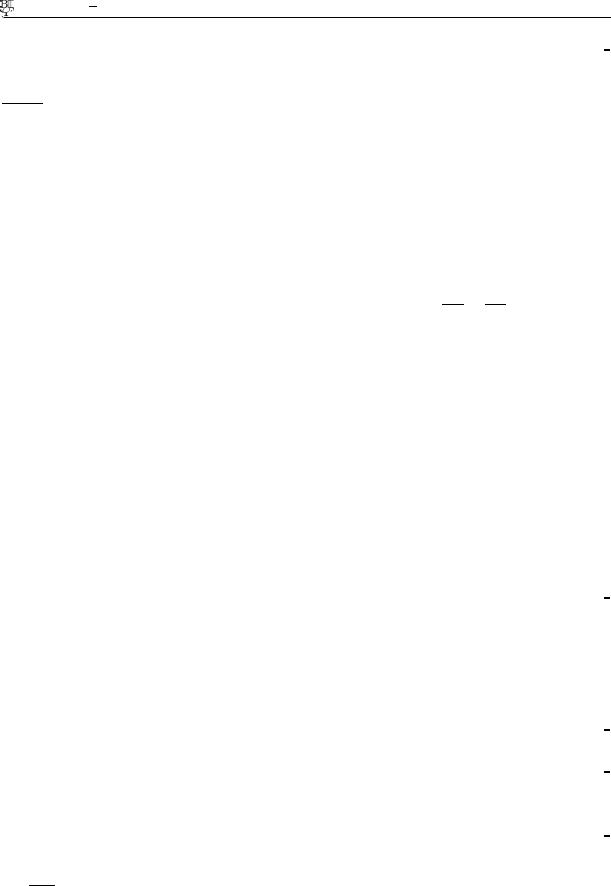
x  y
y
∂2z = 0 ∂x∂y

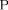





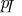



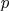













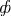
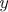


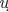

 z = z(x, y)
z = z(x, y) 





 xz − ln(yz) = 1,
xz − ln(yz) = 1, 







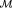








1 ∂z |
+ z |
∂z |
= 0. |
||||
|
|
|
|
|
|||
y ∂x |
∂y |
||||||
|
|
||||||
∂z ∂z
∂x ∂y


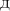




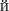






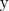
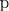







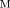 F (x, y, z) = 0
F (x, y, z) = 0
|
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
∂y |
|
|
|
|
|
∂F |
|
|
|
|
|
||||||
|
|
|
= − |
|
∂x |
|
; |
|
= − |
|
|
; |
= 0. |
|
|
|
|||||||||||||||||||||
|
|
|
∂x |
|
∂F |
|
|
|
∂y |
|
∂F |
|
|
|
|
∂z |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
F (x, y, z) = xz − ln(yz) − 1 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
z |
|
|
|
|
|
|
||||
∂z |
|
|
|
|
z |
|
|
|
|
z2 |
|
|
∂z |
|
|
|
|
|
|
|
|
z |
|
|
|||||||||||||
= − |
|
|
= |
|
|
|
|
|
|
= − |
yz |
= |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
∂x |
x − |
y |
1 |
− |
xz |
|
|
∂y |
|
x − |
y |
y(xz |
− |
1) |
|||||||||||||||||||||||
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|||||||||||
1 ∂z |
+ z |
∂z |
= |
1 z2 |
+ z |
z |
= 0, |
|||||
|
|
|
|
|
|
|
|
|
||||
y ∂x |
∂y |
y |
1 − xz |
y(xz − 1) |
||||||||
∂U |
= f (x, y, z) U = f (x, y, z)dx + F (y, z); |
∂x |

|
∂2U |
= f (x, y, z) |
∂U |
= f (x, y, z)dx + F (y, z) |
||
|
∂x2 |
∂x |
||||
U = f (x, y, z)dx dx + F (y, z)x + (y, z). |
||||||
|
|
|
|
|
f |
F |
|
|
|
|
|
|
|
∂2U = 0. ∂x∂y
|
|
∂ |
|
∂U |
= 0 |
|
∂U |
= 0 dx + Φ1(y) = Φ1(y) |
||
|
|
|
|
|
||||||
|
|
∂x |
∂y |
∂y |
||||||
|
U = Φ |
1(y)dy + F (x) = |
Φ(y) + F (x). |
|||||||
|
|
|
|
|
||||||
= Φ(y)+F (x) 
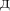
 F
F  Φ
Φ 
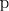








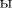

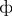
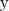











x  y
y



 U (x, y) =
U (x, y) =
U (x, y) = Φ(y) + F (x) |
∂U |
= Φ (y) |
∂2U |
|
= |
∂ |
|
(Φ (y)) = 0. |
∂y |
∂y∂x |
∂x |
||||||
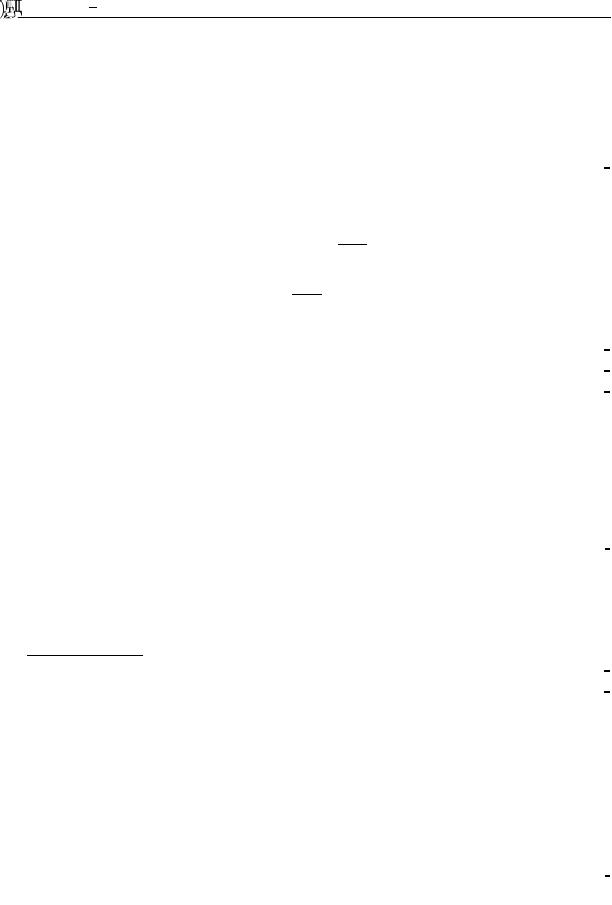
∂U
a1(x1, x2, . . . , xn, U ) ∂x1 + · · · +
∂U
+an(x1, x2, . . . , xn, U ) ∂xn = b(x1, x2, . . . xn, U ).
z = z(x, y) |
|
|
|
|
|
|
|
P (x, y, z) |
∂z |
|
+ Q(x, y, z) |
∂z |
|
= R(x, y, z). |
|
∂x |
∂y |
||||||
|
|
|
|||||
P Q R |
|
|
|
|
|
|
|
P Q R |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
¯ |
¯ |
||
F = P (x, y, z)i + Q(x, y, z)j + R(x, y, z)k.
¯
F
|
|
¯ |
¯ |
|
|
¯ |
|
dr¯ = dx i + dy j + dz k, |
|||||||
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
F |
|
dx |
|
|
dy |
|
dz |
||
|
= |
|
|
= |
|
. |
|
P (x, y, z) |
Q(x, y, z) |
R(x, y, z) |
|||||

F
 N
N
¯
N
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ ¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N · F = 0. |
|
|
|
|
z = f (x, y) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
, |
∂z |
, −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
|||
¯ |
∂z |
¯ |
∂z |
¯ |
¯ |
|
|
¯ |
¯ |
|
|
|
|
|
|
|
N = |
∂x |
i + |
∂y |
j |
− k |
|
|
F |
· N = 0 |
|
|
|
|
|
||
|
|
|
|
P (x, y, z) |
∂z |
+ Q(x, y, z) |
∂z |
− R(x, y, z) = 0, |
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
∂x |
∂y |
|||||||||||



 z = f (x, y)
z = f (x, y) 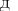







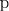




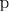







ψ1(x, y, z) = C1, |
ψ2(x, y, z) = C2, |

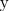












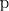








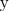







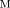




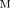


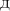
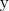


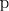

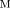


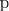

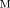
 C1
C1  C2
C2 
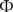 (C1, C2) = 0
(C1, C2) = 0 














































 C1
C1  C2
C2 
 (ψ1(x, y, z), ψ2(x, y, z)) = 0.
(ψ1(x, y, z), ψ2(x, y, z)) = 0.
|
|
|
|
|
|
|
z = f (x, y) |
|
|
U (x, y, z) = 0 |
|
|
|||
∂U |
|
∂U |
|
∂U |
¯ |
¯ |
|
|
|
|
|
|
|
F |
· N = 0 |
∂x |
|
∂y |
|
∂z |
|||
P (x, y, z) ∂U∂x + Q(x, y, z) ∂U∂y + R(x, y, z) ∂U∂z = 0.






 a ∂x∂z + b ∂y∂z = c
a ∂x∂z + b ∂y∂z = c


 a b c
a b c
dxa = dyb = dzc .
bdx = ady |
cdx = adz. |
bx − ay = C1 |
az − cx = C2. |








































 (bx −ay, az −
(bx −ay, az −
−cx) = 0
|
cx |
|
|
z |
z = |
+ ϕ(bx − ay) ϕ |
|
|
|
|
|
|
||
a |
|

|
a1 |
= |
a2 |
= · · · = |
an |
= t |
|
|
|
|
|
|
k1, k2 |
, . . . , kn |
|
|
|
|
||||||||||||||
|
b1 |
b2 |
bn |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k1a1 + k2a2 + · · · + knan |
= t. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
k1b1 + k2b2 + · · · + knbn |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z + y − x) |
∂z |
+ (z + x − y) |
∂z |
= z |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
= |
dy |
|
|
= |
dz |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z + y − x |
z + x − y |
z |
||||||||||
dx + dy |
= |
dz |
d(x + y) = 2dz x + y = 2z + C1 |
x + y − 2z = C1; |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
2z |
z |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−dx + dy |
= |
dz |
|
d(x − y) |
= 2 |
dz |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2(x |
− |
y) |
|
z |
|
x |
− |
y |
|
|
− z |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ln |x − y| = −2 ln |z| + ln C2 (x − y)z2 = C2.
 (x + y − 2z, (x − y)z2) = 0
(x + y − 2z, (x − y)z2) = 0
1(x, y, z) = 0, |
2(x, y, z) = 0. |
|
Ψ1(x, y, z) = C1, |
|
Ψ2(x, y, z) = C2, |
|
|
|
Φ1(x, y, z) = 0, |
|
|
|
|
|
|
|
|
Φ2(x, y, z) = 0, |
|
|
|
|
|
|
|
x y |
z |
C1 C2 |
Φ0(C1, C2) = 0
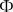 0
0
















 C1
C1  C2
C2