Файловый архив студентов. Файловый архив студентов.
1295 вузов, 5022 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Институт инженерной физики и радиоэлектроники СФУ
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Теория цепей СВЧ.pdf
Скачиваний:
1320
Добавлен:
09.06.2015
Размер:
2.7 Mб
Скачать
☆
►Содержание►

154

емкостного – коэффициентом kC . Эти коэффициенты могут быть вычислены по приближенным формулам (7.37), (7.38). Коэффициент k является «суммой» коэффициентов kL и kC , причем суммирование производится по форму-

ле (7.24).

7.6. Связанные контуры. Энергия и коэффициенты связи

Определения коэффициента связи резонаторов СВЧ, приведенные выше, не удобны для практического применения. Так, использование формул (7.5) и (7.7) для связанных резонаторов требует предварительного нахождения параметров эквивалентной схемы. Кроме того, эти формулы и формула (7.20) задают значение коэффициента связи k лишь на резонансной частоте, в то время как связь между резонаторами фильтра существует на всех частотах ω, где коэффициент прохождения мощности СВЧ отличен от нуля.

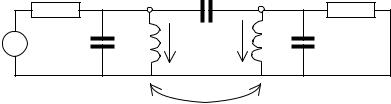
Используя энергетический подход, сформулируем физическое определение коэффициента связи резонаторов, позволяющее исследовать частотную зависимость k(ω). Для этого рассмотрим пару связанных колебательных контуров, включенную между генератором и нагрузкой (см. рис. 7.18).

R1

U1

Cm U2

R2

Є

C1

L1

I1

I2

L2

C2

Lm

Рис. 7.18. Связанные колебательные контуры, включенные между генератором и нагрузкой

Пусть ЭДС генератора изменяется по закону Є(t) = Є0 exp (−iωt). Тогда комплексные напряжения и токи в индуктивностях контуров будут удовлетворять уравнениям

 

 

U1 = −i ω(L1I1 + Lm I2),

 

 

 

(7.39)

 

 

U2 = −i ω(L2I2 + Lm I1),

 

 

 

(7.40)

U

 

−U

 

=

i

 

[I

 

− iωC U

+

U2

] .

(7.41)

 

 

ωC

 

 

R

 

1

 

2

 

m

2

2 2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

155

Из уравнений (7.39)−(7.41) находим коэффициент передачи по напряжению из первого контура во второй:

 

U2

=

 

Lm

L1

−[L2 − L2m

L1

] Cmω2

 

.

(7.42)

U1

 

 

 

 

 

 

 

 

1 −[C

2

+ C

m

+ i (ω R

)][L − L2

L ] ω2

 

 

 

 

 

 

 

 

 

2

 

2

m

 

1

 

 

Видно, что коэффициент передачи обращается в нуль на частоте

ω

p

= L

m

[(L L

2

− L2

)C

m

]

(7.43)

 

 

1

m

 

 

 

и имеет максимум модуля вблизи резонансной частоты второго контура

ω2 =1 L2 (C2 + Cm )[1 − L2m (L1L2 ) ] .

(7.44)

Замечаем, что на резонансной частоте ω2 коэффициент передачи является мнимым числом:

U2

 

= iR2

(C2 + Cm ) Lm

L1

− Cm

.

(7.45)

 

U1

 

 

 

 

 

ω=ω2

L2 [1 − L2m (L1L2)][C2 + Cm ]

 

 

 

 

 

Очевидно, что резонансная частота первого контура

ω1 =1 L1(C1 + Cm)[1 − L2m (L1L2 ) ] .

(7.46)

Запишем выражение для электромагнитной энергии, запасаемой всеми элементами связанных контуров. Начнем с энергии электрического поля:

W

C

(t) = 1

C Re2

(U

) + 1

C

2

Re2 (U

2

) + 1

C

m

Re2 (U

1

−U

2

).

(7.47)

 

2

1

1

2

 

 

2

 

 

 

 

 

Выделяя для комплексных напряжений U1(t), U2(t) амплитуды |U1|, |U2| и начальные фазы ϕ1 = arg(U1)|t = 0 , ϕ2 = arg(U2)|t = 0 , выражение (7.47) записываем в виде

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

WC (t) =WC + WC (t) ,

 

 

 

 

 

 

 

 

 

 

 

 

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 1

(C +C

 

)

 

U

 

 

2 + 1

(C

+C

 

)

 

U

 

 

 

2 − 1

C

 

 

U

 

 

 

 

U

 

 

cos (ϕ −ϕ

) (7.48)

 

W

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

4

1

m

 

 

 

1

 

4

2

 

m

 

 

 

 

2

 

 

2

 

m

 

 

1

 

 

 

 

2

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− постоянная составляющая энергии электрического поля, которую будем называть усредненной по времени энергией;

156

~

(t) = 1 (C +C

 

 

 

)

 

U

 

 

2

cos 2(ωt−ϕ ) +

1

(C

+C

 

)

 

U

 

 

2

cos 2(ωt−ϕ

) −

 

 

 

 

 

 

 

 

 

 

W

C

m

 

 

 

 

m

 

 

 

 

 

4

 

1

 

 

 

 

 

 

 

 

1

 

 

1

4

2

 

 

 

 

2

 

 

2

(7.49)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− 1

C

 

 

U

 

 

 

 

 

U

 

 

 

cos (2ωt−ϕ − ϕ

)

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

 

 

 

 

 

 

2

 

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− переменная составляющая энергии электрического поля, которую будем называть колеблющейся энергией.

Усредненная энергия W¯C , согласно (7.48),

WC =W11C +W22C +W12C ,

где

 

 

 

= 1

(C +C

 

)

 

U

 

 

2

,

 

 

 

= 1

(C

+C

 

)

 

U

 

 

2

(7.50)

 

W

 

 

 

 

W

 

 

 

 

 

 

11C

4

1

m

 

 

 

1

 

 

 

 

22C

4

2

 

m

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− усредненные энергии электрического поля, запасаемые первым и вторым контуром в отдельности;

 

 

 

= −

1

C

 

Re (U *U

 

)

(7.51)

W

m

2

 

 

 

 

12C

2

 

1

 

 

− усредненная энергия электрического поля, запасаемая первым и вторым контуром совместно.

Напротив, колеблющаяся энергия WC , согласно (7.49),

 

 

~

 

~

~

 

~

 

 

 

 

 

 

 

WC (t) =W11C (t) +W22C (t) + W12C (t) ,

 

 

 

где

 

 

 

 

~

 

 

 

 

 

 

~

(t) = 1

(C +C

 

) Re (U 2 ),

(t) = 1

(C

+C

 

) Re (U 2 )

(7.52)

W

m

W

22C

m

11C

4

1

1

 

4

2

 

2

 

− колеблющиеся энергии электрического поля, запасаемые первым и вторым контуром в отдельности;

~

(t) = − 1

C

 

Re (U U

)

(7.53)

W

m

12C

2

 

1 2

 

 

− колеблющаяся энергия электрического поля, запасаемая первым и вторым контуром совместно.

Запишем теперь энергию магнитного поля, запасаемую всеми элементами связанных контуров:

W

L

(t) = 1

L Re2

(I

1

) + 1

L

2

Re2 (I

2

) + L

m

Re (I

1

) Re (I

2

).

(7.54)

 

2

1

 

2

 

 

 

 

 

 

 

Выделяя амплитуды токов |I1|, |I2| и их начальные фазы ψ1, ψ2 , запишем выражение (7.54) в виде

= + ~ ,

WL (t) WL WL (t)

157

где

 

 

 

 

 

= 1 L

 

I

 

 

 

2

+

1

L

 

 

I

 

 

2 + 1

L

 

 

 

I

 

 

 

 

I

 

 

 

cos (ψ

−ψ

 

)

(7.55)

 

 

W

L

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

4

1

 

 

1

 

 

 

 

 

 

4

 

2

 

 

2

 

 

2

 

 

 

 

 

1

 

 

 

 

 

2

 

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− усредненная энергия магнитного поля;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

(t) = 1 L

 

I

 

 

 

2

 

cos 2(ωt−ψ

) + 1

L

 

 

 

I

 

 

2

cos 2(ωt−ψ

 

) +

 

 

 

 

 

 

 

 

 

 

 

 

W

L

 

1

 

 

 

 

2

 

2

 

 

2

 

 

 

 

4

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

(7.56)

 

 

 

 

 

 

+ 1

L

m

 

I

 

 

 

 

I

 

 

 

cos (2ωt−ψ

−ψ

 

)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−колеблющаяся энергия магнитного поля.

Вформулах (7.55)–(7.56), в отличие от формул (7.48) и (7.49), ни одно из слагаемых нельзя отождествлять с энергией, запасаемой каким-либо определенным контуром, так как ток в одном из контуров может быть связан с колебанием в другом контуре. Последнее утверждение становится очевид-

ным, если рассматривать колебания на частоте ω=ωр, когда U2 =0 при U1 ≠0. Действительно, в этом случае колебания во втором контуре отсутствуют (U2 =0), а ток I2, согласно (7.41), отличен от нуля. Это означает, что колебания в первом контуре простираются лишь на один из элементов второго контура (L2), а не на весь второй контур в целом.

Таким образом, ток I2 во втором контуре может быть связан как с колебанием во втором контуре, так и с колебанием в первом контуре. Аналогичная неопределенность имеет место и для тока I1.

Эту неопределенность можно устранить, если учитывать реальную взаимосвязь между токами и напряжениями, выражаемую общими формулами

 

 

 

 

 

 

I1 = i11U1 + i12U2

,

 

 

 

(7.57)

 

 

 

 

 

 

I2 = i21U1 + i22U2.

 

 

 

 

 

 

 

 

Подставляя (7.57) в (7.55), получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

WL =W11L +W22 L +W12 L ,

 

 

где

 

 

 

 

 

 

 

W11L = 14 [L1

 

i11

 

2 + L2

 

i21

 

2 + 2Lm

Re (i11* i21 )]

 

U1

 

2 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

(7.58)

W22 L = 14 [L1 i12 2 + L2 i22 2 + 2Lm Re (i12* i22 )] U 2 2

− усредненные энергии магнитного поля, запасаемые первым и вторым контуром в отдельности;

158

W12 L = 12 Re ([L1i11* i12 + L2i21* i22 + Lm (i11* i22 + i21* i12 )]U1*U 2 )

(7.59)

− усредненная энергия магнитного поля, запасаемая первым и вторым контуром совместно.

Теперь подставим (7.57) в (7.56). Получаем

 

 

~

~

~

 

 

~

 

(t) ,

 

 

 

WL (t)

=W11L (t)

+ W22 L

(t) + W12 L

 

 

где

 

 

Re ([L i2

 

 

 

 

 

 

]U 2 ),

 

~

(t) = 1

+ L

i2

+ 2L

i i

 

 

 

W

21

 

 

11L

4

1 11

2

21

 

m 11

 

1

(7.60)

~

(t) = 1

Re ([L i2

+ L

i2

+ 2L

i i

 

 

]U 2 )

W

22 L

22

 

 

4

1 12

2

22

 

m 12

 

2

 

− колеблющиеся энергии магнитного поля, запасаемые первым и вторым контуром в отдельности;

~

Re ([L1i11i12

+ L2i21i22

+ Lm (i11i22 + i12i21 )]U1U 2 )

(7.61)

W12L (t) = 12

− колеблющаяся энергия магнитного поля, запасаемая первым и вторым контуром совместно.

Из уравнений (7.39)–(7.40) находим коэффициенты

i11 =

 

i L2

ω

 

 

 

 

i12 =

 

− i Lm

ω

 

 

 

 

 

 

 

 

,

 

 

 

 

,

 

 

L L − L2

 

L L − L2

 

 

1 2

 

 

m

 

 

 

 

 

1 2

m

(7.62)

 

 

− i Lm

 

ω

 

 

 

 

 

 

 

i L1

ω

i21 =

 

 

 

 

 

 

i22 =

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

.

 

 

L L − L2

L L − L2

 

 

1 2

 

 

m

 

 

 

 

 

1 2

m

 

Подставляя (7.62) в (7.61), получаем

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

Lm

 

 

 

 

Re (U1U 2 ) .

(7.63)

W12 L

(t) =

 

 

 

 

 

 

 

 

 

 

 

 

 

2ω2 (L1L2

 

 

 

 

 

 

 

 

− L2m )

 

 

 

 

Учитывая, что

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Re (U1U 2 ) =

 

U1

 

 

 

 

U 2

 

cos (2ωt−ϕ1−ϕ2) ,

 

 

 

 

 

 

из формул (7.53) и (7.63) находим амплитуды колеблющихся энергий электрического и магнитного поля, запасаемых контурами совместно:

Амплитуды обеих колеблющихся энергий допускают совместное изменение их знаков, так как амплитудой синусоиды Re(U1U2) можно считать как |U1U2|, так и –|U1U2|.

159

 

W

= − 1 C

 

 

U

 

 

 

 

U

 

 

 

,

W

 

=

 

 

Lm

 

 

 

 

 

U

 

 

 

 

 

U

 

 

.

 

 

 

(7.64)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12C

2

m

 

 

 

1

 

 

 

 

2

 

 

 

 

 

 

12L

 

 

2ω2 (L L

2

− L2

 

)

 

 

 

1

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теперь подставим (7.62) в (7.58). Получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L2

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

L1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

.

(7.65)

W11L =

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

,

W22L =

 

 

 

 

 

 

 

 

 

 

 

 

 

U 2

 

 

4ω2 (L L

2

− L2

)

 

 

 

4ω2

(L L

2

− L2

)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

—

 

запа-

Очевидно, что усредненная энергия электрического поля W12C ,

саемая контурами совместно, есть энергия емкостной связи контуров, а ус-

—

редненная энергия магнитного поля W12L есть энергия индуктивной связи контуров.

Можно предположить, что коэффициенты связи kC и kL пропорцио-

— —

нальны энергиям W12C и W12L. Подобное предположение уже делалось при выводе формул (7.37), где оно достаточно хорошо оправдалось. Однако это не вполне верно. Действительно, если бы коэффициенты kC и kL были про-

― ―

порциональны усредненным энергиям W12C и W12L , то на резонансной частоте ω=ω2 эти коэффициенты, согласно формулам (7.53), (7.63), (7.45) и (7.39)−(7.40), обращались бы в нуль, а не принимали значения, выражаемые формулами (7.22) и (7.23). Поэтому будем искать взаимосвязь коэффициен-

―

―

ֹ

тов kC и kL не с усредненными энергиями W12C

и W12L , а с амплитудами W12C

ֹ

 

 

 

 

 

 

 

 

 

 

и W12L колеблющихся энергий, которые не обнуляются на резонансной частоте.

Используя формулы (7.50), (7.64), (7.65), приходим к равенствам

 

W12C

 

 

 

 

 

− Cm

 

 

(W

+W

)(W

+W

22C

)

=

(C1+Cm)(C2 +Cm) ×

 

11L

11C

22L

 

 

 

 

 

 

(7.66)

 

 

 

 

 

 

 

 

2

 

 

 

 

 

×

 

 

,

 

 

 

 

 

(1+ω2ω−2)(1+ω2ω−2)

 

 

 

 

 

 

 

 

1

2

 

 

 

W12L

 

 

 

=

Lm

2

 

ω2 ) . (7.67)

(W11L+W11C ) (W22L+W22C )

L1L2

(1+ω−2ω2 ) (1+ω−2

 

 

 

 

 

 

 

 

1

2

 

Видно, что при выполнении условий двойного резонанса ω=ω1 =ω2 правые стороны равенств (7.66) и (7.67) совпадают соответственно с правыми сторонами формул (7.22) и (7.23). Поэтому коэффициенты индуктивной и емкостной связи любых резонаторов СВЧ и контуров определяем формулами

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности