4
1. ВОЛНЫ В ЛИНИЯХ ПЕРЕДАЧИ СВЧ
1.1. Типы линий передачи
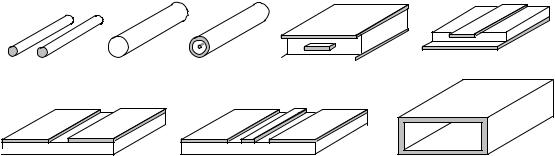
Линия передачи СВЧ есть устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии СВЧ в заданном направлении [1]. Линии передачи могут содержать проводники и диэлектрическое заполнение (см. рис. 1.1) [2].
а |
б |
в |
|
г |
|
д |
е |
ж |
з |
Рис. 1.1. Основные типы линий передачи:
а– двухпроводная; б – диэлектрическая; в – коаксиальная; г – симметричная полосковая;
д– микрополосковая; е – щелевая; ж – копланарная; з – прямоугольный волновод
Порядок связности – это геометрическая характеристика поперечного сечения линии передачи, определяемая числом проводящих поверхностей [1]. В зависимости от количества проводящих поверхностей, линии передачи подразделяют на односвязные линии, двухсвязные, трехсвязные и многосвязные. Линии нулевой связности не имеют проводящих поверхностей. Их называют диэлектрическими линиями передачи.
Регулярная линия передачи – это линия, у которой в продольном направлении неизменны поперечное сечение и электромагнитные свойства заполняющих сред [1]. Если у линии передачи отсутствует хотя бы одно из условий регулярности, то такая линия называется нерегулярной.
Однородной линией передачи называют линию, заполненную однородной средой, то есть средой с неизменными электромагнитными свойствами в каждой точке объема, который она заполняет [1]. Наоборот, неоднородная линия передачи – это линия, заполненная неоднородной средой, то есть средой, в которой существуют две или более области, имеющие разные электромагнитные свойства. Линию передачи без диэлектрического заполнения называют воздушной.
5
Линия передачи может быть как открытой, так и экранированной. В открытой линии передачи электромагнитное поле волны находится не только внутри линии, но и вблизи нее [1]. В экранированной линии выходу электромагнитного поля за ее пределы препятствует металлический экран.
1.2.Общие сведения о волнах в линиях передачи
Влюбой линии передачи можно возбуждать различные типы гармонических волн, отличающиеся структурой электромагнитного поля в поперечном сечении. Бегущей волной называют электромагнитную волну определенного типа, распространяющуюся в линии передачи только в одном направлении [1].
Для каждой из бегущих волн существует своя критическая частота
ωcr, ниже которой она распространяться не может, а лишь локализуется
вблизи своего источника. Критическую частоту ωcr называют еще частотой отсечки. Электромагнитная волна, имеющая наименьшую критическую частоту в данной линии передачи, называется волной основного типа или основной волной. Волной высшего типа называют волну, критическая частота которой выше критической частоты основной волны. Диапазон частот, в котором возможно распространение волн основного типа без распространения волн высших типов называют основным диапазоном частот линии передачи [1].
Важнейшим параметром любой бегущей гармонической волны является волновое число kz, описывающее зависимость напряженностей E и H электромагнитного поля от продольной координаты z линии передачи:
E(x, y, z, t) = E(x, y)eik z z −iωt , H(x, y, z, t) = H(x, y)eik z z −iωt . |
(1.1) |
Волновое число kz также называют постоянной распространения. В общем случае kz – комплексная функция частоты ω, то есть kz(ω) = kz′+ ikz″, где kz′ и kz″ – вещественные функции частоты. Величину kz′ называют коэффициентом фазы, а величину kz″ – коэффициентом затухания. В отсутствие поглощения энергии, то есть при вещественной диэлектрической и магнитной проницаемости заполняющей среды, мнимая часть волнового числа kz″= 0, если частота волны ω>ωcr, и kz″> 0, если ω<ωcr. Вместо
6
волнового числа kz часто используют коэффициент распространения γ, определяемый формулой γ= ikz.
Фазовая скорость гармонической волны связана с вещественной
частью волнового числа соотношением* |
|
v = ω/kz′. |
(1.2) |
В общем случае фазовая скорость волны в линии передачи является функцией частоты. Свойство линии передачи, характеризующее изменение фазовой скорости v в зависимости от частоты ω, называют дисперсией линии передачи.
Скорость передачи сигналов в линии передачи называют групповой скоростью vg. Эта скорость может отличаться от фазовой скорости v, если линия обладает дисперсией. Групповая скорость связана с волновым числом k′ формулой
vg = dω/dkz′. |
(1.3) |
Падающей волной называют бегущую волну, распространяющуюся от выбранного начального сечения вдоль направления распространения. Отраженной волной называют бегущую волну, вызванную отражением от нерегулярности в линии передачи и распространяющуюся в направлении обратном падающей волне. Стоячей волной называют периодическое изменение амплитуды напряженности электрического и магнитного полей вдоль линии передачи, вызванное интерференцией падающей и отраженной волн [1].
Одной из характеристик электромагнитного поля бегущей волны является характеристическое сопротивление. Им называют отношение
Zс = Eτ /Hτ , |
(1.4) |
где Eτ и Hτ – поперечные составляющие напряженностей электрического и магнитного поля бегущей волны. Эту величину не следует путать с волновым сопротивлением .
*Жирным шрифтом выделены номера формул, которые рекомендуется запомнить.
По-английски волновое сопротивление есть characteristic impedance.
7
Волновое сопротивление линии передачи есть отношение
Z = Uпад /Iпад , |
(1.5) |
где Uпад и Iпад − напряжение и ток падающей волны. Его не следует путать и |
|
с входным сопротивлением линии передачи [1]. |
|
Входное сопротивление линии передачи есть отношение |
|
Z(z) = U(z) /I(z), |
(1.6) |
где U(z) и I(z) – комплексные амплитуды напряжения и тока в сечении линии передачи, заданном координатой z. Очевидно, что входное сопротивление будет совпадать с волновым сопротивлением только при отсутствии отраженной волны.
1.3. Общие уравнения для электромагнитных волн
Получим ряд общих уравнений для электромагнитных волн в произвольной линии передачи и на их основе установим некоторые свойства этих волн. Будем исходить из уравнений Максвелла для участка линии передачи, заполненного материалом с относительной диэлектрической проницаемостью ~εr , относительной магнитной проницаемостью μr и про-
водимостью σ. Для простоты будем считать материал изотропным. Тогда ~εr , μr и σ будут не тензорными, а скалярными величинами. Уравнения Максвелла имеют вид [3–4]
rotE = −∂B ∂t , |
(1.7) |
rotH = ∂D ∂t + j, |
(1.8) |
divD = ρ, |
(1.9) |
divB = 0 , |
(1.10) |
где индукции D и B связаны с напряженностями E и H уравнениями |
|
~ |
(1.11) |
D = ε0 εrE , |
|
B =μ0μr H , |
(1.12) |
а ток проводимости j связан с σ уравнением |
|
j = σE. |
(1.13) |
8
Здесь ε0 и μ0 – абсолютные диэлектрическая и магнитная проницаемости свободного пространства.
Будем рассматривать гармонические колебания электромагнитного поля
E(x, y, z, t) =E(x, y, z)e−iωt , H(x, y, z, t) = H(x, y, z)e−iωt . |
(1.14) |
Подставляя (1.14) в (1.7)−(1.8) и используя комплексную диэлектрическую проницаемость
~ |
(1.15) |
εr = εr + iσ/(ε0ω) , |
|
получаем |
|
rot E = iωμ0μr H , |
(1.16) |
rot H = −iωε0εr E. |
(1.17) |
Вычислим ротор от левой и правой части уравнения (1.16), а затем подставим в него равенство (1.17). Используя общее тождество
rot rot F = grad (div F) − F |
(1.18) |
для произвольного вектора F, получаем |
|
grad (div E) − E = k 2E . |
(1.19) |
где |
|
k = εrμr k0, |
(1.20) |
k0 = ω/c |
(1.21) |
− волновое число электромагнитной волны в свободном пространстве; c =1 ε0μ0 − скорость света. С учетом равенства (1.17) и тождества
div rot F = 0 |
(1.22) |
уравнение (1.19) принимает вид уравнения Гельмгольца |
|
E + k 2E = 0 . |
(1.23) |
Аналогичным образом можно получить уравнение |
|
H + k 2H = 0 . |
(1.24) |
Таким образом, электрическая и магнитная составляющие гармонических электромагнитных колебаний удовлетворяют уравнению Гельмгольца.
9
Далее будем рассматривать гармонические колебания, являющиеся волной с волновым числом kz, бегущей вдоль оси z. Учитывая (1.1), запишем уравнения (1.16) и (1.17) покомпонентно:
∂Ez |
− ikz Ey = iωμ0μr H x , |
∂H z |
− ikz H y = −iωε0εr Ex , |
|
|||||||||||
∂y |
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
||
ikz Ex − |
∂Ez |
= iωμ0μr H y , |
ikz H x − |
∂H z |
= −iωε0εr Ey , |
(1.25) |
|||||||||
|
|
||||||||||||||
|
|
|
|
∂x |
|
|
|
|
∂x |
|
|
||||
|
∂Ey |
− |
∂E |
x = iωμ0μr H z , |
|
∂H y |
− |
∂H |
x = −iωε0 |
εr Ez . |
|
||||
|
∂x |
|
|
|
∂x |
|
∂y |
|
|||||||
|
|
|
∂y |
|
|
|
|
|
|
|
|||||
Выразим поперечные составляющие бегущей волны через две продольные. Для этого в первом уравнении левого столбца исключим составляющую Ey с помощью второго уравнения правого столбца:
i (k 2 − kz2 ) H x = ε0εr ω |
∂Ez |
− kz |
∂H z |
. |
(1.26) |
|
|
||||
|
∂y |
∂x |
|
||
Аналогичным образом получаем выражения для остальных поперечных компонент
i(k 2 |
− kz2 ) H y = −ωε0εr |
∂Ez |
− kz |
∂H z |
, |
(1.27) |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
∂x |
∂y |
|
||||
i(k 2 |
− kz2 ) E y = −kz |
∂Ez |
|
+ ωμ0μr |
∂H z |
, |
(1.28) |
|||||
∂y |
|
|
||||||||||
|
|
|
|
|
∂x |
|
||||||
i(k 2 |
− kz2 ) Ex = −kz |
|
∂Ez |
|
− ωμ0μr |
∂H z |
. |
(1.29) |
||||
|
∂x |
|
||||||||||
|
|
|
|
|
∂y |
|
||||||
Таким образом, поперечные составляющие электрического и магнитного поля бегущей волны всегда можно выразить через продольные составляющие. Сами же продольные составляющие с точностью до неопределенных коэффициентов могут быть получены независимо одна от другой решением уравнений (1.23) и (1.24). При этом значение одного из неопределенных коэффициентов можно задать произвольно, а значения остальных – найти из электродинамических граничных условий.
На границе двух сред, ни одна из которых не является идеальным проводником (σ≠∞), электродинамические граничные условия определяются уравнениями
10
ε(r1) En(1) |
− ε(r2) En(2) |
= 0 , |
(1.30) |
μ(r1) H n(1) |
− μ(r2) H n(2) |
= 0 , |
(1.31) |
Et(1) − Et(2) = 0 , |
(1.32) |
||
Ht(1) − Ht(2) = 0 . |
(1.33) |
||
Здесь верхние индексы, взятые в скобки, указывают номер среды. Нижние индексы n и t указывают на нормальные и тангенциальные составляющие векторов. Нормаль n направлена из среды 1 в среду 2. Очевидно, что
врегулярной линии передачи нормаль n всегда перпендикулярна оси z.
Вслучае когда среда 2 является идеальным проводником (σ=∞), то электромагнитное поле внутри нее отсутствует, а на ее поверхности появля-
ются поверхностные заряды ρs и течет поверхностный ток J. При этом уравнения (1.30)−(1.33) принимают вид
εr ε0 En = −ρs , |
(1.34) |
Hn = 0, |
(1.35) |
Et = 0, |
(1.36) |
Ht ×n = J, |
(1.37) |
где нормаль n направлена в глубь идеального проводника.
Таким образом, электродинамические граничные условия состоят из шести скалярных равенств, то есть по одному равенству для каждой составляющей поля. Однако только четыре равенства из шести являются независимыми, если эти равенства налагаются на функции, являющиеся решениями уравнений Максвелла. Обычно накладывают граничные условия на все четыре тангенциальные составляющие электромагнитного поля.
Вернемся к формулам (1.26)−(1.29). Из них видно, что волны в линиях передачи в зависимости от наличия или отсутствия у них продольных составляющих Ez и Hz можно разделить на четыре типа. Сразу оговоримся, что из одного из них можно выделить пятый тип. Рассмотрим каждый из пяти типов волн.