70
Аналогичным образом получаем одиннадцать уравнений для пяти точек соединения проводников (i = 1, 2, … , 5), имеющих координату z =l1 +l2:
|
∑5 |
Uim [eiθ2m X12+m − e−iθ2m X17+m − X 22+m + X 27+m ]= 0, |
(4.67) |
||
|
m =1 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
− Z2 X 2 + ∑U5m [X 22+m − X 27+m ]= |
Z2 a2 , |
(4.68) |
|
|
|
m =1 |
|
|
|
∑5 |
Iim [eiθ2m X12+m + e−iθ2m X17+m − X 22+m − X 27+m ]= 0 |
(i ≠ 5) , |
(4.69) |
|
|
m =1 |
|
|
||
−X 2 |
+ ∑5 |
I5m [eiθ2m X12+m + e−iθ2m X17+m − X 22+m − X 27+m ]= − a2 , |
(4.70) |
||
Z2 |
m =1 |
Z2 |
|
||
где θ2m =km l2 – электрическая длина центрального отрезка для m-й волны. Наконец, пять уравнений для правых концов проводников правого
отрезка, замкнутых на емкости, то есть уравнения для точек с координатой z =l, имеют вид
∑5 [(Iim + iωCiUim )ei θ1m X 22+m + (Iim − iωCiUim )e−i θ1m X 27+m ]= 0 . (4.71) m =1
Уравнения (4.71) получаются из условия (4.61), в котором изменен знак перед током, так как этот ток в случае подключения емкости к правому концу проводника является уже не вытекающим из емкости, а втекающим в нее.
Таким образом, мы записали 32 уравнения для 32-х неизвестных амплитуд Xi . Эта система уравнений решается численно. Затем, так как b1 = X1 и b2 = X2, элементы матрицы в соответствии с определением (4.20) находятся по формулам
S11 |
= X1 |
a |
=1, a |
2 |
=0 , |
S21 = X 2 |
a |
=1, a |
2 |
=0 , |
|||
|
|
|
1 |
|
|
|
1 |
|
(4.72) |
||||
S12 |
= X1 |
|
|
|
|
|
|
S22 = X 2 |
|
|
|
|
|
|
a =0, a |
2 |
=1, |
a =0, a |
2 |
=1. |
|||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||
4.5. Произвольное соединение многополюсников
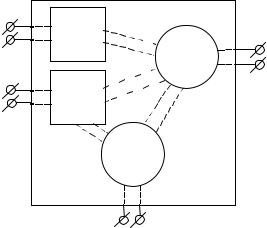
Рассмотрим схему СВЧ, полученную произвольным соединением многополюсников [11]. Пусть схема содержит i внутренних и p внешних вхо-
дов (см. рис. 4.11).
71
1
p
2
Рис. 4.11. Схема СВЧ с i внутренними и p внешними входами
Для всех компонент схемы вектор амплитуд всех выходящих волн b связан с вектором амплитуд входящих волн a соотношением
b =Sa. |
(4.73) |
Строки и столбцы в (4.73) можно перегруппировать так, чтобы волновые переменные разделились на две группы: первая соответствовала бы p внешним входам, а вторая – i входам, соединенным внутри схемы. Тогда уравнение (4.73) можно записать в виде
b p |
S pp |
S pi a p |
, |
(4.74) |
||
|
|
= |
|
|
||
bi |
Sip |
Sii ai |
|
|
||
где bp и ap – волновые переменные, соответствующие p внешним входам; bi и ai − волновые переменные, соответствующие i внутренним входам. Ограничения, накладываемые внутренними соединениями для i внутренних входов, могут быть записаны в виде
bi = Γai , |
(4.75) |
где Γ − матрица соединений, содержащая нули и единицы. Из выражений (4.74) и (4.75) можно получить
Γai = Si p ap + Sii ai |
|
или |
|
ai = (Γ− Si i)−1Si p ap. |
(4.76) |
Подставляя (4.76) в (4.74), получаем |
|
bp = [Spp +Spi (Γ− Si i)−1Si p]ap, |
(4.77) |
72
откуда матрица рассеяния
Sp = Spp +Spi (Γ− Si i)−1Si p. |
(4.78) |
Уравнения (4.76) и (4.75) могут использоваться для получения волновых переменных на внутренних входах при произвольном способе возбуждения внешних входов.
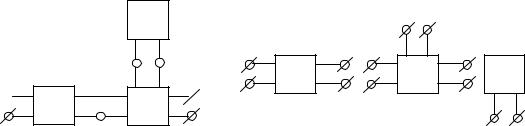
Пример 1. Расчет S-матрицы составной схемы. Рассмотрим схему на рис. 4.12, состоящую из узлов A, В и С. Матрицы рассеяния составляющих компонентов обозначим SA, SB и SC.
C |
|
|
|
6 |
1 A 2 |
3 |
|
5 |
1 B 2 |
C |
1 A 2 
3 B 4 
Рис. 4.12. Составная схема и ее компоненты A, B и C
Запишем параметры всех трех компонентов схемы в виде (4.74):
b |
|
|
A |
0 | |
A |
0 |
0 |
0 |
a |
|
||||
|
1 |
|
|
S11 |
S12 |
|
1 |
|
||||||
b4 |
|
|
0 |
S22B | 0 |
0 |
S23B S21B |
a |
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
− − + − − − − |
− |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
= S A |
0 | S A |
0 |
0 |
0 |
a |
2 |
. |
|||||
|
|
|
|
21 |
|
|
22 |
|
|
|
|
|
|
|
b |
|
|
0 |
0 |
| |
0 |
S |
C |
0 |
0 |
a |
6 |
|
|
|
6 |
|
|
|
|
|
||||||||
b |
|
|
0 |
B |
| 0 |
0 |
B |
B |
a |
5 |
|
|||
|
5 |
|
|
S32 |
S33 |
S31 |
|
|
||||||
b |
|
|
0 |
B |
| 0 |
0 |
B |
B |
a |
3 |
|
|||
|
3 |
|
|
S12 |
S13 |
S11 |
|
|
||||||
Матрица соединений Γ может быть записана в виде
b2 0 0 0 1 a2b6 = 0 0 1 0 a6 .b5 0 1 0 0 a5b3 1 0 0 0 a3
(4.79)
(4.80)
73
Полную матрицу рассеяния находим по формуле (4.78), используя (4.79) и (4.80):
|
|
|
|
|
|
|
|
− S A |
0 |
|
0 |
1 |
−1 |
|
A |
|
|
|
|
A |
0 |
|
|
A |
0 0 0 |
|
|
22 |
− S |
C |
1 |
0 |
|
S21 |
0 |
|
|
S p = S11 |
|
+ S12 |
|
|
0 |
|
|
|
0 |
0B |
. (4.81) |
|||||||
|
0 S22B |
|
0 |
0 S23B S21B |
|
|
0 |
1 |
|
− S33B − S31B |
|
0 |
S32 |
|
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
|
B |
B |
|
|
0 |
B |
|
|
|
|
|
|
|
|
|
|
|
− S13 |
− S11 |
|
|
S12 |
|
|||
Пример 2. Расчет S-матрицы схемы, один из входов которой нагружен.
Пусть схема A, описываемая матрицей SA, имеет p+1 вход. Требуется рассчитать матрицу SВ схемы B, которая получается подключением к (p+1)-му входу схемы A нагрузки с импедансом Z. Объединенная матрица схемы A и нагрузки Z имеет вид
|
A |
| |
A |
0 |
|
|
|
|
|
S pp |
S pi |
|
|
|
|||
− |
+ |
− |
− |
, |
(4.82) |
|||
[S]= |
A |
| |
A |
0 |
|
|||
Sip |
Sii |
|
|
|
||||
|
0 |
| |
0 |
S |
Z |
|
|
|
|
|
|
|
|
||||
где SZ – параметр рассеяния нагрузки Z; i указывает на вход, к которому подключена нагрузка Z. Матрица соединений Γ может быть записана в виде
b |
|
0 1 a |
|
(4.83) |
|
i |
|
= |
i |
, |
|
b |
|
1 0 a |
|
|
|
|
|
|
|
|
|
где ai и bi – волновые переменные для нагруженного входа i схемы A; a и b − волновые переменные для нагрузки Z. Подставим (4.82) и (4.83) в общую формулу (4.78):
SB = S App + [S Api |
0] − SiiA |
1 Z −1 |
SipA |
. |
(4.84) |
||
|
1 |
− S |
|
0 |
|
|
|
После выполнения произведения матриц получаем |
|
|
|
||||
SB = S App + |
1 |
|
|
S ApiSipA . |
|
(4.85) |
|
(S Z )−1 − SiiA |
|
||||||
|
|
|
|
|
|||
Вычислим параметр рассеяния для нагрузки Z. Будем исходить из того, что ток I и напряжение U на нагрузке Z связаны равенством
U/I = Z.