Рух планет. Закони Кеплера.

На початку XVII ст. німецький вчений Іоганн Кеплер після 20-літнього опрацювання даних спостереження датського вченого астронома Тихо Браге за рухом планет встановив закони їх руху, які лягли в основу небесної механіки:

I-й закон: Планети обертаються навколо Сонця по плоским кривим еліпсам, в одному із фокусів яких знаходиться Сонце.

II-й закон: Радіус вектор, який проведений від Сонця до планети, за однаковий проміжок часу описує рівні площі. (Закон площ).

III-й закон: Квадрати часу обертання планет навколо Сонця відносяться, як куби великих півосей їх орбіт.

Вивід закону всесвітнього тяжіння.

Відкриття законів Кеплера, кінематичних законів небесної механіки, поставило певну механічну задачу: найти силу, під дією якої здійснюється рух планет.

І.Ньютон, маючи геніальну інтуїцію, зміг відкрити Загальний закон всесвітнього тяжіння. Він показав, що закони Кеплера та основні закони динаміки дозволяють зробити висновок про існування сили тяжіння планет до Сонця, яка прямо пропорційна масам планет, і обернено пропорційна квадрату їх відстані від Сонця.

Щоб спростити міркування, уявимо, що планети рухаються по круговим орбітам(це припущення близьке до істини).

Дійсно по третьому закону Кеплера:

Так як планети рухаються по круговихм орбітам, то:

, ,, тоді

, ,,,

, ,,,

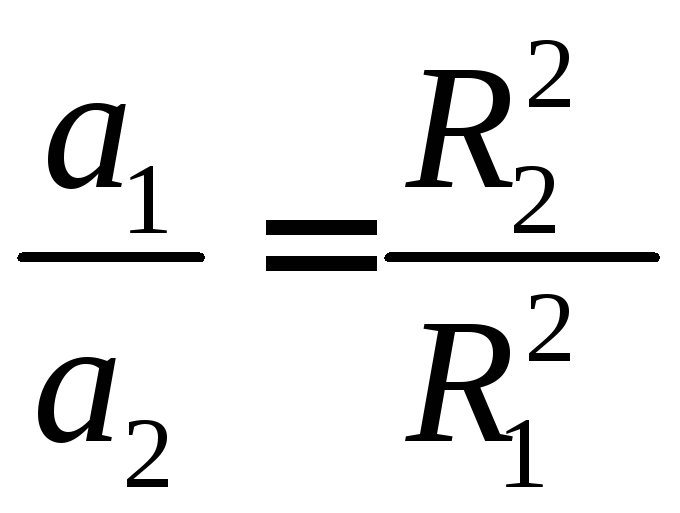Сила, яка діє на планету зі сторони Сонця, обернено пропорційна квадрату відстані планети від Сонця і прямо пропорційна її масі.

k – коефіцієнт пропорційності маси системи.

Відповідно до III закону Ньютона: F_{пл_Сонце} = –F_{Сонце_пл}

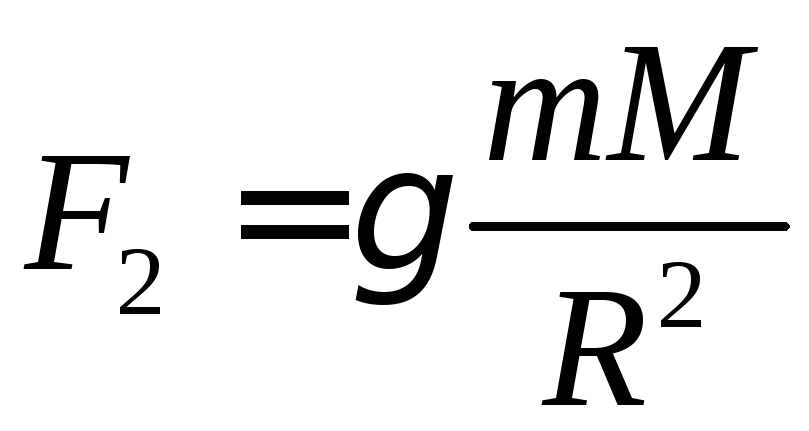
Об’єднуючі ці дві формули, отримуємо закон, якому підкоряється гравітаційна взаємодія (всесвітнє тяжіння), вперше відкритий та сформульований англійським вченим І.Ньютоном в 1687р. в «Математичних початках натуральної філософії».

Закон тяжіння Ньютона.

Ньютон вперше відкрив фактичне існування у природі гравітаційних взаємодій. Всім тілам в природі властиво притягуватися один до одного. Сила взаємодії двох матеріальних точок прямо пропорційна добутку мас взаємодіючих точок і обернено пропорційно квадрату відстані між ними:

–коефіцієнт пропорційності, який називається гравітаційною постійною.

Сила тяжіння відноситься до фундаментальних взаємодій.

У законі всесвітнього тяжіння Ньютона був узагальнений ряд часткових експериментальних факторів (порівняння величини прискорення, особливості руху планет).

Для перевірки закону, Ньютон провів дослідження руху комет, рух супутників планет Юпітера і Сатурна.

Багаторазові перевірки в умовах Землі показали, що він справедливий для всіх випадків взаємодії тіл, і взаємне притягання тіл – універсальна властивість і прояв в усьому, що нас оточує у світі.

Закони всесвітнього тяжіння встановлені для тіл, які прийняті за матеріальні точки.

Гравітаційна постійна та її вимірювання

Гравітаційна постійна чисельно дорівнює силі, з якою два тіла одиничної маси притягуються, розташовані на відстані 1 м один від одного.

Чисельне значення вперше отримане англійським вченим Кавендишем (1798р).

Складність такого досліду полягала у тому, що сили, які діють між тілами у будь-якому експерименті дуже малі. Першу думку висловив Ньютон:

Рис. 6.7.

;

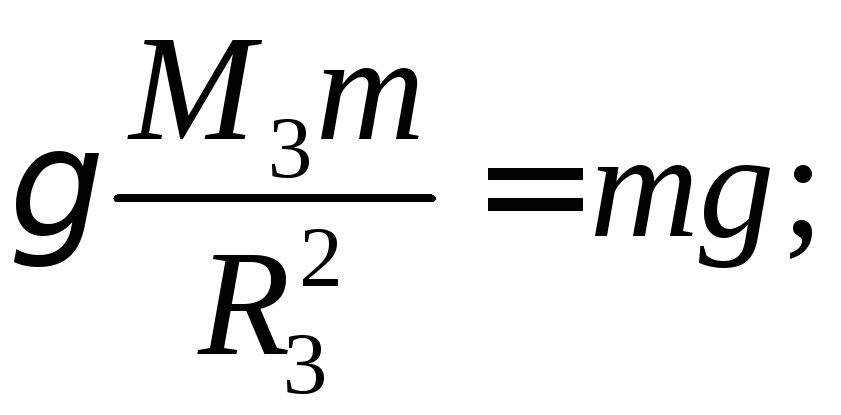
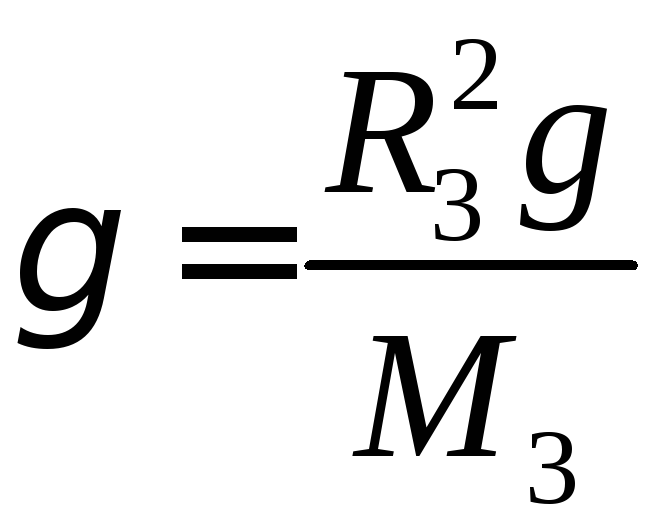= 6,67*10^-11 Hм²/кг;

Дослід Кавендиша з обертовими вагами (рис. 6.7).

Постійна тяжіння відноситься до світових фундаментальних констант. Вона характеризує, з кількісного боку, фундаментальну властивість матерії – гравітацію.

Поле тяжіння та його характеристика.

Сили тяжіння відносяться до фундаментальних гравітаційних взаємодій. На питання про походження сил тяжіння, фізика поки ще не може відповісти. Але незважаючи на це:

а) Закон всесвітнього тяжіння має велику сферу застосування: він справедливий для тіл, які знаходяться в спокої, або повільно рухаються.

б) Закон всесвітнього тяжіння вказує лише, від чого залежить сила взаємного притягання тіл, а не пояснює механізм передачі дії на відстані через вакуум.

Згідно з сучасною картиною світу, будь-яка взаємодія тіл, у тому числі і гравітаційна, на відстані, здійснюється через особливий матеріальний посередник – силове поле, яке називається гравітаційним полем або полем тяжіння.

Рис. 6.8.

Для кількісної характеристики гравітаційного поля в кожній його точці вводиться фізична величина – напруженість гравітаційного поля. Вона вимірює силу з якою поле тяжіння діє на пробне тіло одиничної маси, яке знаходиться в данні точці поля (рис. 6.8).

;

; ;;

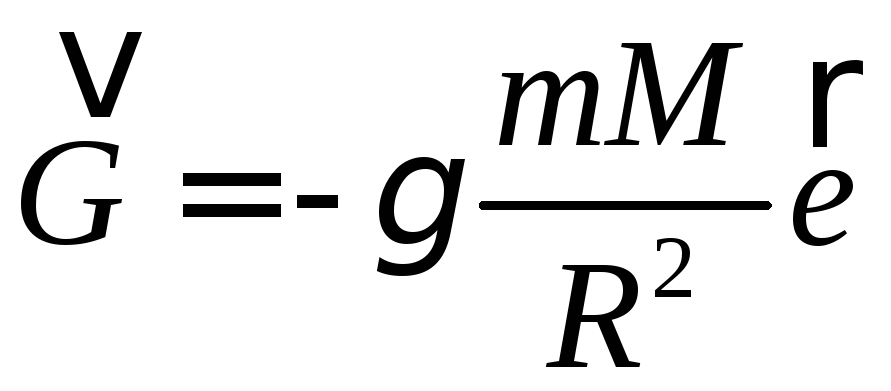Вектор напруженості направлений до центру, в котрому покладений токчовий заряд поля. Таке поле називається центральним.

;
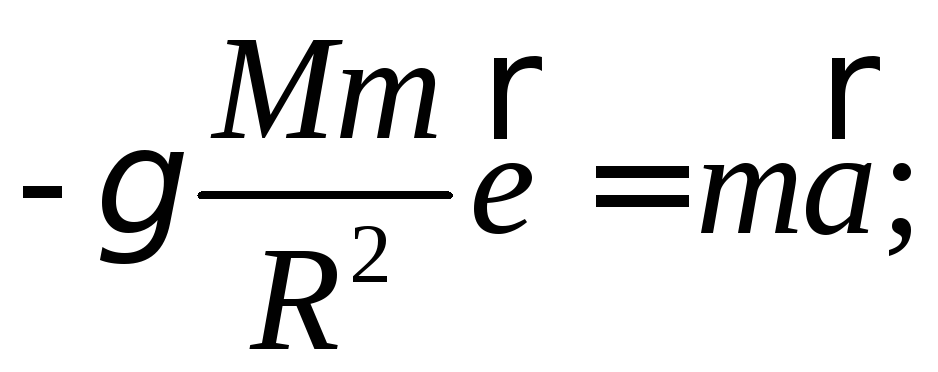