Елементи ств Ейнштейна. Релятивістська механіка.

15. Власний час життя μ-мезону дорівнює 2 мкс. Від точки народження до точки розпаду в лабораторній системі відліку мю-мезон пролетів відстань l = 6 км. З якою швидкістю (в частинах швидкості світла) рухався мезон ?

16. Показати, що формула додавання швидкостей релятивістських частинок переходить у відповідну формулу класичної механіки при .

17. Дві релятивні частинки рухаються в лабораторній системі відліку зі швидкостями = 0,6с та = 0,9с вздовж однієї прямої. Визначити їх відносну швидкість у двох випадках: 1) частинки рухаються у одному ж і тому напрямку; 2) частинки рухаються в протилежних напрямках.

18. Прискорювач надав радіоактивному ядру швидкість = 0,4с. В момент вильоту з прискорювача ядро викинуло в напрямку свого руху -частинку зі швидкістю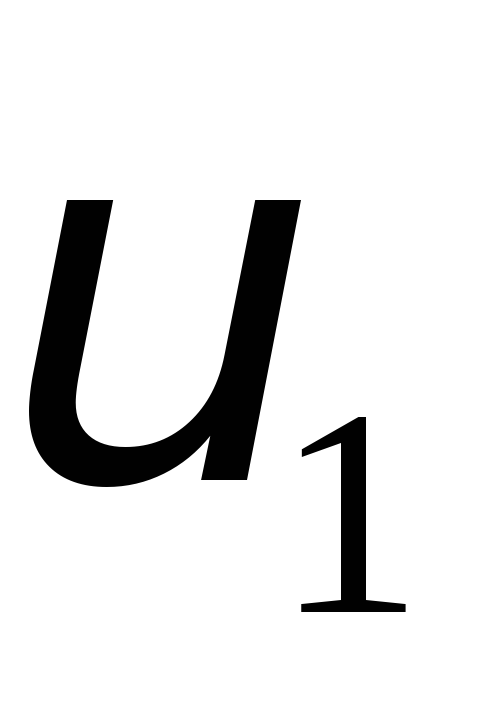= 0,75с відносно прискорювача. Знайти швидкість частинки відносно ядра.

19. Два прискорювача викидають назустріч один одному частинки зі швидкостями = 0,9с. Визначити відносну швидкість зближення частинок в системі відліку, яка рухається разом з однією із частинок.

20. Частинка рухається зі швидкістю = 0,5с. В скільки разів релятивістська маса частинки більша маси спокою?

21. З якою швидкістю рухається частинка, якщо її релятивістська маса в три рази більша маси спокою?

22. Відношення заряду електрона, який рухається, до його маси, визначене із досліду, дорівнює 0,88·10¹¹ Кл/кг. Визначити релятивістську масу т електрону та його швидкість .

23. На скільки відсотків релятивістська маса частинки більша маси спокою при швидкості = 30 Мм/с ?

24. Показати, що вираз релятивістського імпульсу переходить у відповідний вираз імпульсу у класичній механіці при .

25. Електрон рухається зі швидкістю 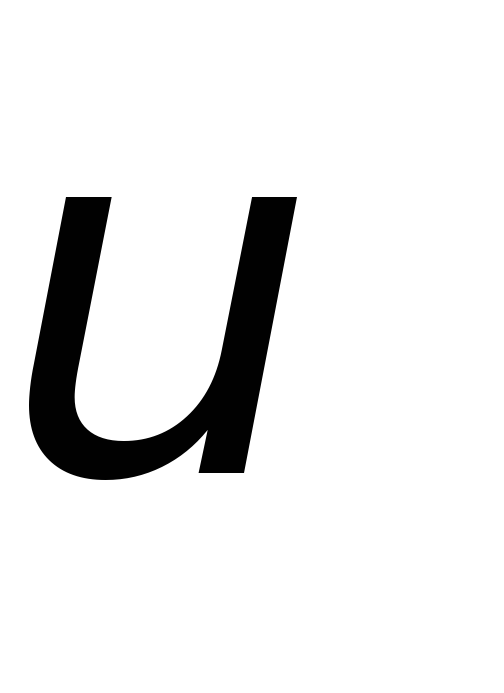= 0,6с. Визначити релятивістський імпульс p електрону.

26. Імпульс р релятивістської частинки дорівнює т₀с (т₀ – маса спокою). Визначити швидкість частинки (в часкинах швидкості світла).

27. Повна енергія тіла зросла на = 1 Дж. На скільки при цьому зміниться маса тіла?

28. Визначити, на скільки повинна збільшитись повна енергія тіла, щоб його релятивістська маса зросла на = 1 г?

29. Визначити енергію спокою: 1) електрона; 2) протона; 3) -частинки; Відповідь подати в одиницях вимірювання джоулях та мегаелектрон-вольтах

30. Відомо, що об’єм води в океані дорівнює 1,37·10⁹ км. Визначити, на скільки зросте маса води в океані, якщо температура води збільшиться на= 1^оС. Густина води в океані прийняти рівною 1,03·10³ кг/м.

31. Кінетична енергія Т електрона дорівнює 10 МеВ. В скільки разів його релятивістська маса більша від маси спокою? Зробити такі ж розрахунки для протона.

32. В скільки разів релятивістська маса протона більше релятивістської маси електрона, якщо обидві ці частинки мають одинакову кінетичну енергію Т = 1 ГеВ?

33. Електрон летить зі швидкістю = 0,8с. Визначити кінетичну енергію Т електрона (в мегаелектрон-вольтах).

34. При якій швидкості кінетична енергія будь-якої частинки речовини дорівнює її енергії спокою?

35. Визначити швидкість електрона, якщо його кінетична енергія дорівнює: 1)Т = 4 МеВ; 2) Т = 1 кеВ.

36. Знайти швидкість протона, якщо його кінетична енергія дорівнює: 1)Т = 1 МеВ; 2) Т = 1 ГеВ.

37. Визначити імпульс р частинки (в одиницях т₀с), якщо її кінетична енергія дорівнює енергії спокою.

38. Визначити кінетичну енергію Т релятивістської частинки (в одиницях т₀с), якщо її імпульс р = т₀с.

39. Кінетична енергія релятивістської частинки дорівнює її енергії спокою. В скільки разів зросте імпульс частинки, якщо її кінетична енергія збільшиться в n = 4 рази?

40. Імпульс р релятивістської частинки дорівнює т₀с. Під дією зовнішньої сили імпульс частинки збільшився у два рази. У скільки разів зросте при цьому енергія частинки: 1) кінетична; 2) повна?