Практичне заняття 6.2 Тема: Елементи ств Ейнштейна. Релятивістська механіка. Основні формули та методичні рекомендації

При вирішенні всіх задач з СТВ використовуються дві початково синхронізовані інерціальні системи координат з взаємно паралельними осями: лабораторна система координат (К-система) і руається відносно неї з постійною швидкістю уздовж осі Ох система координат – К', яка називається власною системою координат.

1. Формула Лоренца скорочення довжини:

,

Де l₀ – власна довжина; ;с – швидкість світла у вакуумі.

2. Релятивістське співвідношення часу:

,

де ∆t₀ – власний час, що відповідає стану спокою рухомої СВ

()

3. Релятивістський закон додавання швидкостей:

4. Релятивістська маса і релятивістський імпульс:

; ,

де m₀ – маса спокою тіла (частинки).

5. Релятивістська форма II закону Ньютона :

6. Повна і кінетична енергія релятивістської частинки :

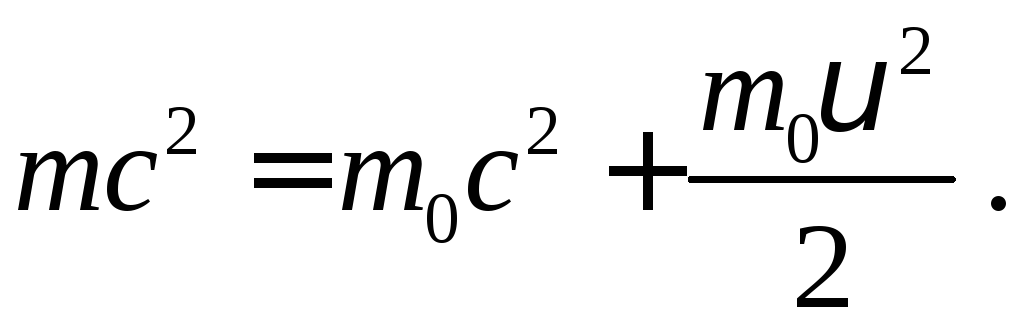
7. Закон взаємозв’язку маси і енергії :

.

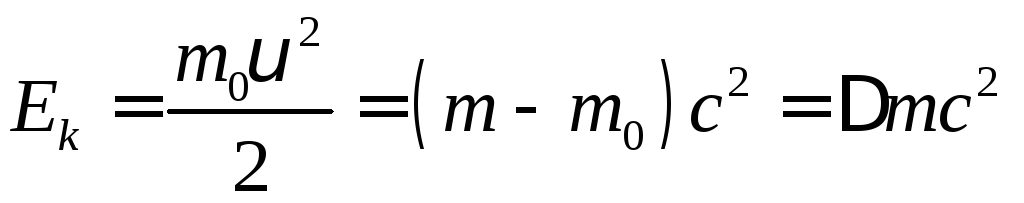Приклади розв’язування задач

Приклад 1. Частинка рухається зі швидкістю = 0,5с. У скільки разів релятивістська маса частинки більша маси спокою?

Розв’язання.

Релятивістська маса частинки рівна

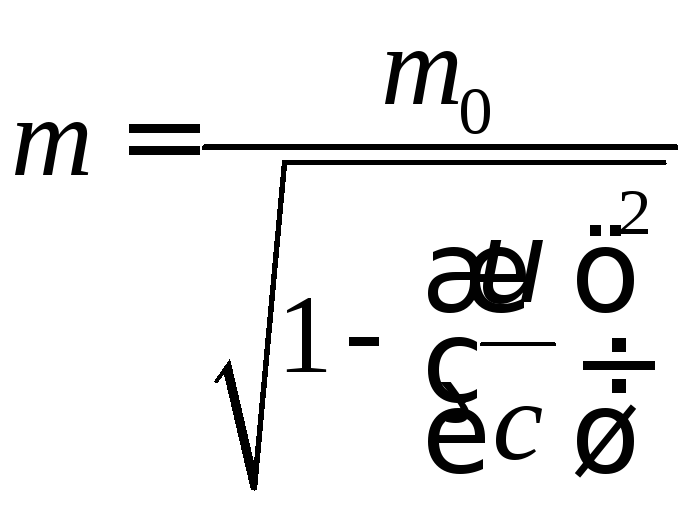
Звідси шукана величина дорівнює

Підставивши числові значення отримаємо

= 1,15.

Приклад 2. Стержень рухається вздовж нерухомої лінійки з деякою постійною швидкістю. Якщо зафіксувати положення обох кінців стержня одночасно в системі відліку, що зв’язана з лінійкою, то різниця відліків на лінійці становить = 4 м. Якщо положення обох кінців зафіксувати одночасно в системі відліку, що зв’язана зі стержнем, то різниця відліку по лінійці складатиме= 9 м. Знайти власну довжину стержня та його швидкість відносно лінійки.

Розв’язання.

Позначимо через L власну довжину стержня. У нерухомій системі відліку його довжина в разів менша.

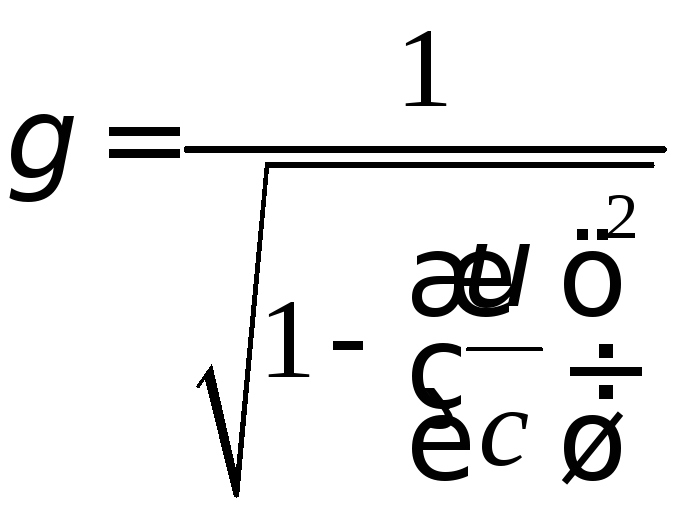
Тобто, .

Якщо ж на лінійці точки фіксуються одночасно в системі стержня, то відстані між поділками лінійки зменшені у разів і відстань між поділками:

Вирішимо отриману систему рівнянь. Поділимо рівняння один на одне і отримаємо формулу для розрахунку іL:

;

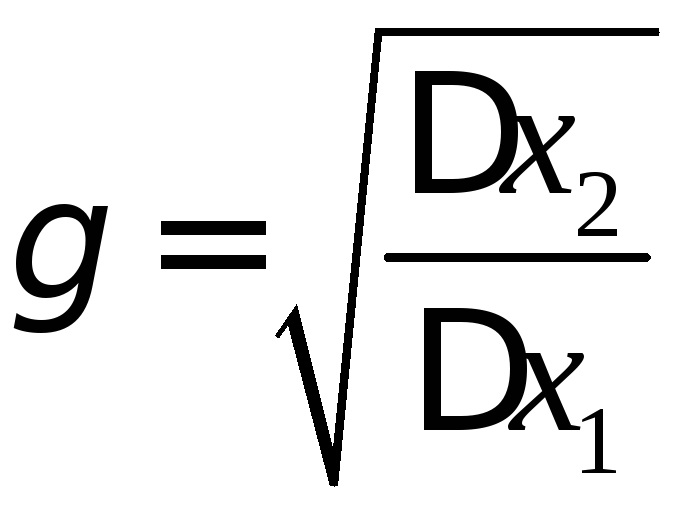З формули для можна виразити швидкість, яка рівна

Підставивши числові значення, отримаємо:

= 6 м; = 0,75с.

Приклад 3. Знайти власну довжину стержня, якщо в лабораторній системі відліку його швидкість = 0,5с, довжина l = 1 м і кут між ним та напрямком руху = 45°.

Розв’язання.

Рис. 1.

Спроектуємо довжину стержня на осі Ох та Оу лабораторної системи координат К (рис. 1):

У вибраних системах координат лоренцівсь­кого скорочення зазнає тільки Х-компонента довжини стержня. Відповідно,

та , де

Квадрат власної довжини знаходиться з теореми Піфагора (рис. 1.) за формулою:

.

Звідси, нарешті, для власної довжини стержня отримаємо:

= 1,08 м.

Приклад 4. Власний час життя деякої нестабільної частинки = 10 нс. Знайти шлях, який пролетить ця частинка до розпада в лабораторній системі відліку, де час її життя становить= 20 нс.

Розв’язання.

Лоренцівське гальмування ходу часу становить

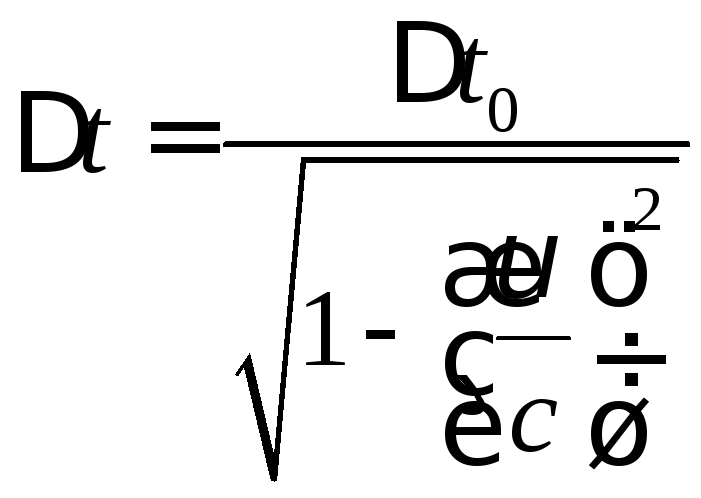
Звідси знайдемо швидкість частинки .

;

;

Знайшовши швидкість, можемо розрахувати шлях, який пройде частинка:

Підставивши числові значення, отримаємо:

= 5,196 м.