Енергія, імпульс і маса фотона.

Фотонами називають найдрібніші частинки світла, або кванти світла. Корпускулярні, або квантові, властивості світла проявляються, наприклад, у явищах фотоефекту або при дослідженні тиску світла. Фотон, як і будь-яка інша матеріальна частинка, має масу, імпульс та енергію.

І все-таки фотон відрізняється від інших частинок тим, що завжди рухається зі сталою швидкістю, яку ніяк не можна змінити.

Швидкість фотона дорівнює швидкості світла, і вона однакова в усих інерціальних системах відліку.

Але тоді з’являються певні утруднення з масою. При релятивістська маса прямує до нескінченності згідно з формулою

Але цього не може бути! Можна припустити, що маса спокою m₀ дорівнює нулю, і це цілком слушно. Дослід підтверджує, що маса спокою фотона в багато разів менша від маси електрона: m₀<4·10^-21 m_e.

Висновок: частинка з нульовою масою спокою завжди рухається зі швидкістю світла.

Проте маса руху, тобто інертна маса, у фотона є.

Спочатку визначимо інші характеристики фотона: енергію та імпульс. Енергія фотона, як відомо, залежить від частоти електромагнітної хвилі ν:

E=h ν,

де h = 6,626·10^-21 Дж·с – стала Планка.

Імпульс фотона знайдемо, скориставшись зв’язком енергії та імпульсу:

Оскільки m₀ = 0, то імпульс фотона

А тепер можна знайти і масу фотона, бо його імпульс p=mc. Маса фотона:

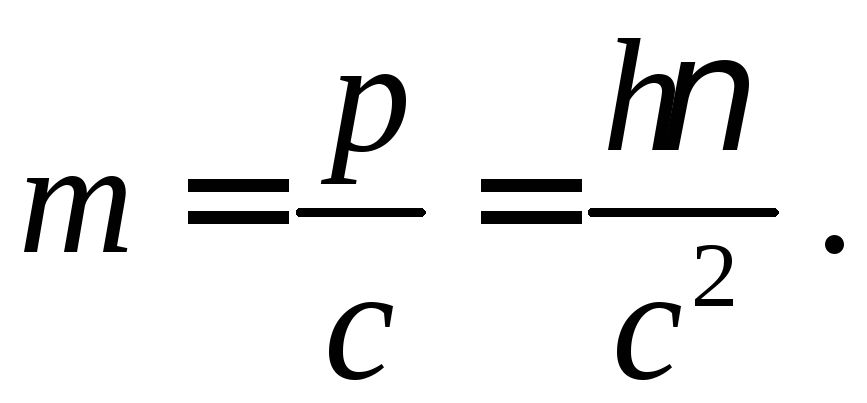
Практичне заняття 6.1 Тема: Неінерціальні системи. Методичні рекомендації та основні формули

Покажемо на декількох прикладах методи рішення задач в неінерціальних системах, тобто в системах, де закони Ньютона, а отже, і всі закони класичної механіки, якими ми користувалися до цих пір, справедливі тільки в припущенні, що окрім сил, зумовлених взаємодією з другими конкретними тілами, діють так звані сили інерції. Сили інерції залежать перш за все від характеру руху неінерціальної системи; це означає, що для їх розрахунку необхідно знати, як рухається неінерціальна система відносно будь-якої інерціальної системи, тобто знати характер руху, його кінематичні параметри.

Сили інерції прямо пропорційні масі даного тіла, отже, прикладені вони, як правило, до центра мас тіла.

Ми розглянемо тільки два типи неінерціальних систем: 1) системи, які рухаються поступально, прямолінійно і прискорено; 2) системи, що обертаються з постійною кутовою швидкістю відносно якої-небудь інерціальної системи (наприклад, відносно Землі). У першому випадку на будь-яке тіло масою m діятиме сила інерції ,де – прискорення неінерціальноїсистеми. У другому випадку діють відцентрова сила інерції , направленатак само, як радіус-вектор , даної матеріальної точки, проведений від осі обертання до точки , і сила інерції Коріоліса, де– швидкість матеріальної точки відносно неінерціальної системи, що обертається .

У задачах, в яких йде мова про фізичні явища, що відбуваються усередині прискорено рухомого тіла (вагону, ліфта і т. д.), рішення, запропоноване на застосуванні другого закону Ньютона, спрощується, якщо розглядати явище в неінерціальній системі відліку, пов’язаній з тілом яке рухається прискорено. Відповідно двом рухам тіла – поступальному і обертальному – застосовують як поступально рухомі, так і не інерціальні системи відліку, що обертаються. У поступально рухомих неінерціальних системах відліку другий закон Ньютона виражається рівнянням:

(1)

Це ж рівняння застосовується і в системах відліку, що обертаються, за умови, що дана матеріальна точка (частинка) знаходиться у ній у стані спокою. Тоді у виразі ,– доцентрове прискорення точки всистемі відліку, що обертається, в якій знаходиться дана частинка; величину називають відцентровою силою інерції.

Сила інерції, що входить в рівняння (1), відрізняється від інших сил тим, що вона існує тільки в неінерціальній системі відліку і для неї не можна вказати тих конкретних тіл, з боку яких вона діє.

Рис. 1.

Існує інший спосіб пояснити поведінку тіла в неінерціальній системі відліку, яка рухається поступально (або, яка обертаєть­ся, якщо дана матеріальна точка знаходиться в ній у стані спокою). При цьому ніяких сил інерції не вводять, але вважають, що відбувається зміна поля тяжіння: прискорення сили тяжіння змінюється за модулем і напрямом та замість g стає рівним g', причому

, (2)

де – прискорення точки неінерціальної системи відліку (відносно інерціальної), в якій знаходиться дана точка (рис. 1). На рисунку 1: –прискорення вагону відносно Землі, g' – прискорення частинки відносновагону. У системі відліку, пов’язаній з вагоном, поле тяжіння таке, що лінія нахилу (напрям вектора g') виявляється нахиленою до помостів вагону, а сила тяжіння відрізняється від тієї, що була в нерухомому вагоні. Цей метод пояснення поведінки тіл в неінерціальних системах відліку отримав обґрунтування в загальній теорії відносності.

З двох розглянутих методів другий набагато швидше приводить до цілі в тих випадках, коли шукана величина визначається в інерціальній системі відліку якою-небудь відомою формулою, що містить прискорення сили тяжіння. Тоді досить прийняти це прискорення рівним величині g', що виражається рівнянням (2), і провести необхідні обчислення. Сюди відносяться задачі на розподіл тиску в рідині або газі в прискорено рухомих посудинах, на коливання математичного або фізичного маятника в прискорюваних кабінах і т.д.