
- •Введение
- •1. Комплексные числа
- •1.1.Комплексные числа и действия над ними
- •1.2. Геометрическое изображение комплексных чисел на плоскости
- •1.3. Тригонометрическая форма комплексного числа
- •1.4. Показательная форма комплексного числа
- •2. Функции комплексной переменной
- •2.1. Множества точек на комплексной плоскости
- •2.2. Функция комплексной переменной
- •2.5. Геометрический смысл модуля и аргумента производной
- •2.6. Элементарные функции
- •2.7. Свойства действительной и мнимой части аналитической функции
- •3. Интегрирование функций комплексной переменной
- •3.1. Определение и вычисление интеграла по комплексной переменной
- •3.2. Вычисление интегралов
- •3.3. Интегральные теоремы Коши
- •3.4.Интегральная формула Коши
- •4.Функциональные ряды
- •4.1.Основные свойства равномерно сходящихся функциональных рядов
- •4.2. Бесконечная дифференцируемость аналитических функций
- •4.4. Разложение функций в ряд Тейлора
- •4.5. Разложение функций в ряды Лорана
- •5.1. Определение особых точек. Вид ряда Лорана в окрестности И.О.Т.
- •5.2. Классификация изолированной особой точки
- •5.3. Вычет функции в изолированной особой точке
- •5.4. Основные теоремы о вычетах
- •5.5. Вычисление определенных интегралов с помощью вычетов
- •6. Элементы операционного исчисления
- •6.1.Определение оригинала, изображение оригинала
- •6.2. Свойства преобразования Лапласа
- •6.3. Нахождение оригиналов
- •Литература

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
n |
|
|
ходится. При z =1 ряд расходится. При z ¹1 , но |z|=1, ряд å |
| z | |
сходится, на основании |
||||||||||||||||||
n |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
||
признака Дирихле (полагая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
= |
( b |
> b |
> .....,limb |
= 0 )), |
|
|
|||||||||||||
|
|
|
||||||||||||||||||
n |
|
|
n |
n |
|
n+1 |
|
|
|
|
|
n |
|
|
|
|
|
|||
а |
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
z - z |
n+1 |
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Sn = |
åzk |
|
|
= |
|
|
< |
|
|
|
, z ¹1 . |
|
|
|||||||
|
|
1- z |
|1 |
- z | |
|
|
||||||||||||||
|
|
k =1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Свойства степенных рядов.
Так как степенные ряды частный случай функциональных рядов, то они обладают всеми свойствами сходящихся функциональных рядов, в частности сумма степенного ря- да в круге его сходимости является аналитической функцией, степенные ряды можно по- членно интегрировать, дифференцировать в круге сходимости, радиусы полученных сте- пенных рядов совпадают с радиусом сходимости исходного степенного ряда.
4.4. Разложение функций в ряд Тейлора
∞
Предположим, что ряд åcn (z - z0 )n сходится в круге | z - z0 |< R к функции f (z), тогда
n=0
получим, что
c0 = f (z0 ),c1 = f ¢(z0 ), n!cn = f (n) (z0 ) ,
т.е.
cn = f (n) (z0 ) ,n = 0,1,2,K . n!
Числа cn называются коэффициентами Тейлора функции f (z), а степенной ряд с этими ко- эффициентами называется рядом Тейлора функции f (z) по степеням (z - z0 ) . Если z0 = 0 ,
то ряд называется рядом Маклорена. Имеет место теорема о разложении функции в ряд Тейлора.
Теорема. Если функция f (z) |
аналитическая в круге | z - z0 |< R , то она однозначно |
|||||||
представляется в нем своим рядом Тейлора |
|
|
|
|||||
|
|
|
∞ |
|
|
|
|
|
|
f (z) = åcn (z - z0 )n , | z - z0 |< R , |
|||||||
Где |
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c = |
f (n) (z0 ) |
= |
1 |
! |
f (η)dη |
, 0 < r < R . |
||
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
n! |
|
|
2πi |
ò |
(η - z0 ) |
n+1 |
||
|
|
|
|z−z0|=r |
|
|
|||
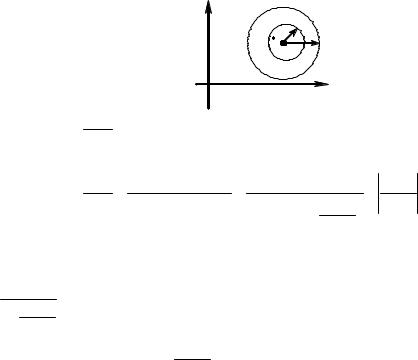
Доказательство. Пусть z произвольная точка внутри круга | z - z0 |< R (рис.4.1). Вы- |
||||||||
берем число r, так чтобы выполнялось неравенство 0 < r < R |
и точка z лежала в круге |
||||
| z - z0 |< r . По интегральной формуле Коши получим |
|
||||
f (z) = |
1 |
!ò |
f (η)dη |
. |
(4.9) |
2πi |
η - z |
||||
|
|
γ r |
|
||
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
z r |
R |
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
0 |
Рис.4.1. |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представим дробь |
1 |
в виде: |
|
|
|
|
|
|
|
|
|
η - z |
|
|
|
|
|
|
|
|
|
|
1 |
= |
1 |
= |
1 |
z - z0 |
|
, |
z - z0 <1, |
|
|
η - z |
|
(η - z0 ) - (z - z0 ) |
|
æ |
- |
ö |
|
η - z0 |
|
|
|
|
|
(η - z0 )ç1 |
|
÷ |
|
|
||
|
|
|
|
|
è |
|
η - z0 ø |
|
|
|
т.к.
| z - z0 |<| η - z0 | .
1
Дробь 1- z - z0 можно рассматривать как сумму бесконечно убывающей геометрической
η - z0
прогрессии со знаменателем q = z - z0 , следовательно
η - z0
1 |
|
1 |
∞ |
æ z - z |
0 |
ök |
∞ |
(z - z |
)k |
|
|
|
= |
|
åç |
|
÷ |
= å |
|
0 |
(4.10) |
||
|
|
|
|
|
k +1 |
||||||
η - z |
|
η - z0 k=0 |
è |
η - z0 ø |
k =0 |
(η - z0 ) |
|
||||
Ряд (4.10) при каждом фиксированном z, равномерно сходится по η для всех ηÎ γz , дейст-
вительно
|
|
|
|
|
|
|
|
|
|
|
|
|
(z - z |
0 |
)k |
|
|
1 | z - z |k |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
£ |
|
|
× |
|
0 |
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(η - z0 )k +1 |
|
r |
|
rk |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
∞ |
| z - z0 |
|k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Числовой |
ряд å |
|
|
|
сходится как |
|
геометрическая прогрессия со |
знаменателем |
|||||||||||||||||||||||||
r |
k |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
)k |
||
|
| z - z |
0 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z - z |
|||
|
|
|
<1 |
, по критерию Вейерштрасса равномерно сходится по η ряд å |
|
0 |
, т.к. |
||||||||||||||||||||||||||
|
r |
|
|
|
k +1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
f (η)(z - z0 )k |
k=0 |
(η - z0 ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
| f (η) |£ M , ηÎ γr , то равномерно сходится и ряд å |
|
|
|
|
|
|
и его можно почленно ин- |
||||||||||||||||||||||||||
(η - z0 ) |
k+1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|||||
тегрировать. В результате интегрирования формула (4.9) принимает вид |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
f (η) |
|
|
|
1 |
|
|
|
|
æ |
∞ |
(z - z0 )k |
ö |
|
|
|
|||||
|
|
|
|
|
|
|
f (z) = |
|
! |
|
dη = |
|
|
|
! f (η)ç |
å |
|
|
|
|
÷dη = |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k +1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2πi |
ò |
|
η - z |
|
|
|
2πi |
ò |
|
ç |
|
|
|
|
|
÷ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
γ r |
|
|
|
γr |
|
è k =0 (η - z0 ) |
ø |
|
|
|
|||||||||||||
∞
= åсk (z - z0 )k ,
k =0
где
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
|
|
с |
= |
1 |
! |
f (η)dη |
, k = 0,1,2,K. |
(4.11) |
|||||||
|
|
|
|
|
|
||||||||||
|
|
k |
|
|
|
|
|
k +1 |
|
|
|
|
|||
|
|
|
|
|
|
2πi |
ò |
(η − z0 ) |
|
|
|
|
|||
|
|
|
|
|
|
γr |
|
|
|
|
|
|
|
||
Ранее получено, что |
c = |
f (k) (z |
0 |
) |
|
. Полученное разложение единственно. |
Действительно, |
||||||||
|
|
|
|
||||||||||||
|
k |
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
если имеется другое разложение |
|
|
|
|
|
− z0 ) |
k |
, |
|
|
|||||
|
|
|
|
% |
|
|
|
||||||||
|
f (z) = åck (z |
|
|
|
|
||||||||||
то так как |
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
% |
|
f (k) (z0 ) |
, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ck = |
|
|
|
|
|
|
|
k!
то
c%k = ck .
Следствие из теоремы Тейлора. Теорема Тейлора доказывает справедливость раз- ложения аналитической функции в круге. Если функция f(z) аналитическая в области G и z0 G , то f(z) можно разложить в ряд по степеням (z − z0 ) , который будет сходится к f (z)
в круге
| z − z0 |< Rz0 ,
где
Rz0 = min | η − z0 |,η ГD .
Ряды Тейлора для элементарных функций.
Справедливы равенства
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
n |
|
|
|
|
|
|
∞ |
|
|
|
z |
n |
|
|
|
|
|
|
|
||||||||
ez =1+ z + |
|
|
|
|
|
+K + |
|
+K = å |
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
n! |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
2n+1 |
|
|
|||||||||
|
|
|
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
|
z |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||||||||
sin z = z − |
|
|
+ |
|
|
|
|
−K = å |
(−1)n |
|
|
|
|
|
|
|
|
|
, |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(2n + |
1)! |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
5! |
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
z |
4 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
z |
2n |
|
|
|
|
|
|||||||||
cos z =1− |
|
|
|
+ |
|
|
|
−K = å |
(−1)n |
|
|
|
|
|
, |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2n)! |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
4! |
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
z |
5 |
|
|
|
|
|
|
|
|
|
∞ |
|
z |
2n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
shz = z + |
|
|
|
|
+ |
|
|
|
|
|
+K = |
|
|
å |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
(2n +1)! |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
3! |
|
|
|
|
|
5! |
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
z |
4 |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
chz =1+ |
|
|
|
|
|
+ |
|
|
|
|
+K = |
å |
z |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2! |
|
|
|
|
|
4! |
|
|
|
|
|
|
|
|
|
n=0 |
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Эти ряды сходятся для любых значений z. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
z |
n |
|
|
||||||||||
ln(1+ z) = z − |
|
|
|
|
|
+ |
|
|
−K = å(−1)n+1 |
|
|
, |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α(α −1) |
|
|
|
|
|
|
|
|
α(α −1)(α − 2)(α − n +1) |
|
|||||||||||||||||||
(1+ z)α = 1+ αz + |
|
z2 +K+ |
|
|
zn +K = |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=1+ å |
α(α −1)(α − 2)K(α − k +1) |
zk , |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=1− z + z2 + z3 +K = å(−1)k zk , |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
1+ z |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=1+ z + z2 +K = åzk . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1− z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Эти ряды сходятся в круге | z |<1.
Доказательство этих разложений такие же, как в обычном анализе.
При решении задачи разложения функции в ряд Тейлора часто применяются искусствен- ные приемы, рассмотрим примеры.
Пример. Разложить в ряд Тейлора в окрестности точки z0 = 0 функцию
z |
. Найти радиус сходимости ряда. |
f (z) = z2 - 2z - 3 |
Решение. Разложим данную функцию на элементарные дроби методом неопределен- ных коэффициентов:
z |
|
= |
z |
= |
A |
|
+ |
B |
|
= |
A(z - 3) + B(z +1) |
. |
z2 - 2z - 3 |
|
(z +1)(z - 3) |
|
z + |
1 |
|
z - |
3 |
|
(z +1)(z - 3) |
||
Из тождества z = A(z − 3) + B(z +1) , полагая последовательно z = −1, z = 3 , находим
A = 14 , B = 34 ,
т.е.
f (z) = 14 × z 1+1 + 34 × z 1- 3 .
Преобразуем правую часть равенства следующим образом:
|
|
|
|
|
|
|
|
|
f (z) = 1 |
× |
|
1 |
|
- |
1 |
× |
1 |
|
|
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
+ z |
|
|
z |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
4 |
|
1- |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
Используя разложение функции |
|
|
|
|
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1+ z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
( |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
1 |
æ |
|
|
z |
|
|
z |
2 |
ö |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
||||||||||||
f (z) = |
|
|
|
1 |
- z + z2 - z3 +K |
|
- |
|
ç1 |
+ |
|
|
+ |
|
|
+K÷ |
= |
||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
è |
|
|
3 |
|
9 |
ø |
|
||||||
|
1 |
æ |
4 |
|
z + |
8 |
z |
2 |
|
28 |
|
z |
3 |
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
ç - |
|
|
|
|
|
|
- |
|
|
|
+K÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
3 |
|
9 |
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Радиус сходимости можно определить двумя способами. Ряд в первой скобке сходится в круге | z |<1, ряд во второй скобке в круге | z |< 3. Оба ряда сходятся в круге | z |<1, поэтому
радиус сходимости R=1.
Второй способ определения R следует из формулы для
|
1 |
!ò |
f (η)dη |
||
cn = |
|
|
|
. |
|
2πi |
(η - z0 ) |
n+1 |
|||
|
γr |
|
|
||
Радиус сходимости R равен расстоянию от центра круга z0 до ближайшей точки ηÎ γr при которой знаменатель обращается в нуль. В нашем случае z0 = 0 , а точка η = −1. По-
этому радиус сходимости равен
| η - z0 |=| -1|=1. |
|
|
1 |
|
|
Пример. Разложить в ряд Тейлора в окрестности точки z0 |
= 3 функцию f (z) = |
|
. |
||
3 |
- 2z |
||||
|
|
|
Решение. Преобразуем данную функцию следующим образом:
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

|
|
1 |
|
|
= |
|
|
1 |
|
|
= |
|
|
1 |
|
= |
||||
|
3 - 2z |
|
3 - 2(z - 3 + 3) |
-3 - 2(z - 3) |
||||||||||||||||
= |
1 |
|
× |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
1+ |
2 (z - 3) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Используя разложение для f |
(z) = |
1 |
получим. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
1+ z |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
∞ |
|
2 |
|
n |
|
|
||
f (z) = |
|
= - |
× å(-1)n çæ |
÷ö |
|
(z - 3)n . |
||||||||||||||
3 |
- 2z |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
n=0 |
è 3 |
ø |
|
|
|
|||||||
Ряд сходится в круге | z - 3 |< 32 .
При разложении в ряды Тейлора отношения двух функций, ряды Тейлора которых извест- ны, полезно применять метод неопределенных коэффициентов. Суть метода рассмотрим на конкретном примере. Теоретической основой метода является единственность разло- жения функции в ряд Тейлора.
Пример. С помощью метода неопределенных коэффициентов найти первые три от- личные от нуля члена разложения функции f(z)=tgz в окрестности точки z=0.
Решение. tgz = cossin zz . По методу неопределенных коэффициентов, справедливо равен-
ство
cossin zz = a0 + a1z + a2 z2 + a3z3 + a4 z4 +K .
Здесь a0,a1,a2 ,…- неопределенные коэффициенты.
Так как функция tg z, нечетная, то a0 = a2 = a4 =K = a2n = 0 .
Учитывая известные разложения для функций sinz, cosz получим тождество:
z - |
z |
3 |
|
z |
5 |
|
z |
7 |
æ |
|
z |
2 |
|
z |
4 |
|
z |
6 |
ö |
( |
a z + a z3 |
+ a z5 |
) |
. |
|
|
+ |
|
- |
|
+K = ç1 |
- |
|
+ |
|
+ |
|
-K÷ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3! |
5! |
7! |
ç |
2! |
4! |
6! |
÷ |
1 |
3 |
5 |
|
||||||||||||||
è |
ø |
|
|
|
|
|
|
||||||||||||||||||
После преобразований, приравнивая коэффициенты при одинаковых степенях z, получим уравнения для неизвестных коэффициентов a1,a3,a5 :
z |
|
1 = a1 |
|
a1 |
|
|
|
|||||
|
|
|
|
|
||||||||
z3 |
|
- |
1 |
= - |
+ a |
|||||||
|
|
|
|
|||||||||
|
|
3! |
|
2! |
3 |
|||||||
|
|
|
|
a3 |
||||||||
z5 |
|
|
1 |
= a + |
a1 |
- |
||||||
|
|
|
|
|
||||||||
|
|
5! |
|
5 |
4! |
2! |
||||||
|
|
|
|
|||||||||
Решая эту систему, получим
a1 =1, a3 = 13 , a5 = 152 .
Следовательно
tgz = z + 13 z2 + 152 z5 .
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
