Министерство образования и науки Российской Федерации Федеральное агентство по образованию

Московский государственный институт электронной техники (технический университет)

_____________________________________________________________

А.М. Терещенко

Теория функций комплексной переменной

Учебное пособие

Утверждено редакционно-издательским советом института

Москва 2006

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Введение

Операции, которые рассматриваются в математике, можно разделить на два класса: прямые и обратные. Так, действию сложения соответствует обратное действие – вычита- ние, умножению – деление, возведению в целую положительную степень – извлечение корня. Совокупность чисел целых и дробных, называемых рациональными числами, будет замкнутой по отношению к первым четырем основным действиям алгебры: сложению, вычитанию, умножению и делению, т.е. при выполнении любого из этих действий над двумя любыми рациональными числами (кроме деления на нуль), мы в результате полу- чим элемент это же совокупности – рациональное число. Извлечение корня в простейшем случае квадратного корня, с одной стороны, дает нам примеры новых чисел, действитель- ных, но не рациональных, называемых иррациональными, а, с другой стороны, чисел вида

y−1 , где y – действительное число. Числа вида y−1 где y – любое действительное число, не равное нулю, называют чисто мнимыми. Приведенные примеры показывают, что обратные операции приводят с необходимости расширения понятия числа. При реше-

ние квадратного уравнения az2 + bz + c = 0 , где a,b,c – действительные числа, корнями мо- гут быть числа вида x + y−1 , где x, y – действительные числа. Такие числа называются

комплексными. В случае y = 0 комплексное число обращается в действительное.

В настоящем пособии будут рассмотрены свойства функций комплексной перемен-

ной z = x + y−1 . Функции комплексной переменной находят многочисленные приложе- ния как в прикладных математических дисциплинах (теоретическая физика, гидродина- мика, теория упругости), так и в различных разделах математики: алгебре, аналитической теории чисел, дифференциальных уравнениях, теории рядов, преобразованиях Фурье, Ла- пласа. Особенно широкое применение методы теории функций комплексной переменной нашли в теории электрических цепей. Раздел теории функций комплексной переменной – операционное исчисление – является одним из основных математических инструментов решения различных задач из области автоматики и телемеханики.

Основное внимание в данном пособии уделяется методам ТФКП, которые имеют большое применение в прикладных задачах – разложения в ряды, вычисление интегралов с помо- щью вычетов, методы операционного исчисления. Для того, чтобы студенты могли само- стоятельно в полном объеме овладеть методами ТФКП, в пособии приведено большое ко- личество примеров с решениями, что дает возможность не только глубже усвоить теоретический материал, но и приобрести необходимые практические навыки в решении задач.

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

1. Комплексные числа

1.1.Комплексные числа и действия над ними

Определение. Комплексным числом называется пара действительных чисел x и y взятых в определенном порядке z = (x, y) . Если y = 0 , то соответствующую пару (x, 0)

отождествляют с действительным числом x . Таким образом, совокупность всех действи- тельных чисел является частью совокупности всех комплексных чисел. Для комплексных чисел определены понятия равенства и арифметические операции следующим образом:

z1 × z2 = (x1x2 - y1y2, x1y2 + x2 y1) .

Пользуясь введенными определениями, можно проверить, что действия над ком- плексными числами обладают свойствами:

а) Ассоциативности

i2 = i ×i = (0,1) ×(0,1) = (-1, 0) = -1. Любое комплексное число (x, y) можно представить ра- венством:

Равенство z = x + iy называется алгебраической формой комплексного числа. Число x

x − iy называется сопряженным с комплексным числом z = x + iy и обозначается z , т.е. z = x − iy

что z × z = z × z =| z |2 .

Введем операцию деления комплексных чисел. Для любых двух комплексных чисел

раические формы z1 = x1 + iy1, z2 = x2 + iy2 , получим

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Эту формулу можно не запоминать, надо помнить, что она получается умножением числителя и знаменателя на число, сопряженное знаменателю. При умножении необходи-

мо учитывать, что i2 = −1, и все операции проводить по обычным правилам алгебры.

1.2. Геометрическое изображение комплексных чисел на плоскости

Выберем на плоскости прямоугольную систему координат. Всякое комплексное число z = (x, y) = x + iy изображается точкой на плоскости с координатами x и y (рис.1.1).

x

0 x

Рис.1.1.

Такое соответствие между комплексными числами и точками плоскости является вза- имно однозначным. При этом действительные числа изображаются точками оси абсцисс, а чисто мнимые – точками оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат – мнимой осью. Плоскость, на которой изображают комплексные числа, называют комплексной плоскостью. Комплексное число z изображается также век- тором с началом в точке 0 и проекциями x и y на координатные оси. Длина вектора z, рав-

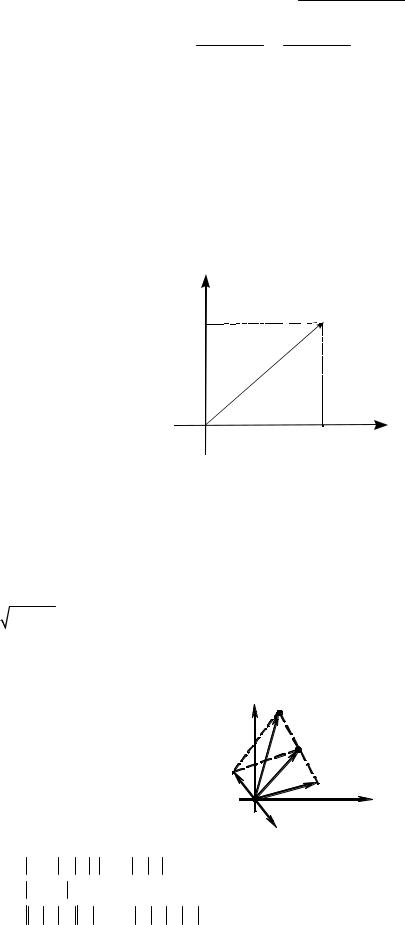
на x2 + y2 равна модулю комплексного числа, в этом состоит геометрический смысл мо- дуля комплексного числа | z |. Из геометрической интерпретации комплексных чисел следуют ряд полезных выводов и неравенств (рис.1.2).

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

1.3. Тригонометрическая форма комплексного числа

Положение точки на комплексной плоскости однозначно определяется расстояни- ем точки от начала координат r =| z | и углом ϕ между действительной осью и вектором z, относительно положительного направления действительной оси (рис.1.3). Этот угол назы- вается аргументом комплексного числа z(z ¹ 0) , и обозначается arg z. Для числа z=0, arg z не определен. Из рис.1.3

y

r y

j

Рис.1.3.

видно, что

Следовательно, любое комплексное число z ¹ 0 можно представить в виде

Запись комплексного числа в виде (1.4) называется тригонометрической формой ком- плексного числа. Для нахождения аргумента комплексного числа надо решить систему

уравнений

−π < α ≤ π . Это значение называется главным и обозначается arg z, другие значения аргу- мента задаются равенством Argz = arg z + 2kπ .

Для главного значения аргумента справедливы соотношения:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com