
- •Тестовые задания к первой главе
- •Две матрицы называются равными, если равны их
- •Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется
- •Построение обратной допускает матрица
- •Построение обратной допускает матрица
- •Тестовые задания ко второй главе.
- •Взаимно перпендикулярными векторами являются
- •Тестовые задания к третьей главе.
- •Уравнение прямой с угловым коэффициентом имеет вид:
- •Уравнение прямой, проходящей через данную точку имеет вид:
- •Уравнение прямой, проходящей через две точки имеет вид:
- •Общее уравнение прямой имеет вид:
- •Уравнение прямой в отрезках имеет вид:
- •Нормальное уравнение прямой имеет вид:
- •Полярное уравнение прямой имеет вид:
- •Каноническое уравнение гиперболы, у которой расстояние между фокусами равно 10 и действительная ось равна 8, имеет вид:
- •Каноническое уравнение параболы, в случае, когда расстояние между фокусом и вершиной равно 3 имеет вид:
- •Общее уравнение плоскости имеет вид:
- •Уравнение плоскости в отрезках на осях имеет вид:
- •Нормальное уравнение плоскости имеет вид:
- •Точки, в которых нарушается непрерывность функции, называются
- •Если в точке разрыва функции существуют конечные пределы функции слева и справа, то эта точка называется точкой
- •Первым замечательным пределом является предел
- •Вторым замечательным пределом является предел
|
|
|
|
470. |
Проверить, |
принадлежат |
ли |
|
|
прямые |
x - 4 |
= |
y + 2 |
= |
z |
и |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x + 1 |
|
|
|
y + 1 |
|
z - 5 |
|
|
|
|
|
|
|
|
|
1 |
|
3 |
1 |
|
|||||||||
|
= |
|
= |
плоскости x - 2 y - 1 = 0 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Тестовые задания к четвертой главе. |
|
|
|
|
|
|||||||||||||
Задание { 1 }. |
Уравнение плоскости, |
проходящей через данную точку пер- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= |
(A; B; C ), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
пендикулярно вектору n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
- : Ax + By + Cz = 0 , |
|
- : A(x - x0 ) + B(y - y0 ) + C(z - z0 ) + D = 0 , |
||||||||||||||||||||||||||||
- : Ax + By + Cz + D = 0 , |
- : A(x - x0 ) + B(y - y0 ) + C(z - z0 ) = 0 . |
|||||||||||||||||||||||||||||
Задание { 2 }. Общее уравнение плоскости имеет вид: |
|
|
|
|
|
|||||||||||||||||||||||||
- : |
x |
+ |
y |
+ |
z |
= 0 , |
|
|
- : |
x |
+ |
y |
+ |
z |
= 1, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
||||||||||||||||||
|
|
a |
|
b |
c |
|
|
|
|
|
a |
|
|
c |
|
|
|
|
|
|||||||||||
- : Ax + By + Cz + D = 0 , |
|
- : Ax + By + Cz = 0 . |
|
|
|
|
|
|||||||||||||||||||||||
Задание { 3 }. Уравнение плоскости в отрезках на осях имеет вид: |
||||||||||||||||||||||||||||||
- : |
x |
+ |
y |
+ |
z |
= 1, |
|
|
- : |
x |
+ |
y |
+ |
z |
= 0 , |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
a |
|
b |
c |
|
|
|
|
|
a |
|
b |
|
c |
|
|
|
|
|
||||||||||
- : Ax + By + Cz = 0 , |
|
|
- : Ax + By + Cz + D = 0 . |
|||||||||||||||||||||||||||
Задание { 4 }. Нормальное уравнение плоскости имеет вид: |
|
|
|
|
|
|||||||||||||||||||||||||
- : Ax + By + Cz + D = 0 , |
|
- : |
x cos a + y cos b + z cos g = 1 , |
|||||||||||||||||||||||||||
- : Ax + By + Cz = 0 , |
|
|
- : |
x cos a + y cos b + z cos g = p . |
||||||||||||||||||||||||||
Задание { 5 }. |
Общее уравнение плоскости проходящей через начало коор- |
|||||||||||||||||||||||||||||
динат имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
- : Ax + By + D = 0 , |
|
|
- : D + By + Cz = 0 , |
|
|
|
|
|
||||||||||||||||||||||
- : Ax + By + Cz = 0 , |
|
|
- : Ax + By + Cz + D = 0 . |
|||||||||||||||||||||||||||
Задание { 6 }. |
Общее уравнение плоскости проходящей через ось аппликат |
|||||||||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : Ax + By = 0 , |
|
|
|
|
- : Ax + Cz = 0 , |
|
|
|
|
|
||||||||||||||||||||
- : By + Cz = 0 , |
|
|
|
|
- : Ax + By + Cz = 0 . |
|
|
|
|
|
||||||||||||||||||||
Задание { 7 }. |
Общее уравнение плоскости проходящей через ось ординат |
|||||||||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : Ax + By = 0 , |
|
|
|
|
- : Ax + Cz = 0 , |
|
|
|
|
|
||||||||||||||||||||
- : By + Cz = 0 , |
|
|
|
|
- : Ax + By + Cz = 0 . |
|
|
|
|
|
||||||||||||||||||||
Задание { 8 }. |
Общее уравнение плоскости проходящей через |
ось абсцисс |
||||||||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : Ax + By = 0 , |
|
|
|
|
- : Ax + Cz = 0 , |
|
|
|
|
|
||||||||||||||||||||
- : By + Cz = 0 , |
|
|
|
|
- : Ax + By + Cz = 0 . |
|
|
|
|
|
||||||||||||||||||||
106
Задание { 9 }. |
Условие |
перпендикулярности |
|
|
двух |
плоско |
||||||||
A1 x + B1 y + C1 z + D1 = 0 и A2 x + B2 y + C2 z + D2 |
= 0 |
имеет вид: |
|
|||||||||||
- : |
A1 |
= |
B1 |
= |
C1 |
, |
- : A A + B B + C C |
2 |
= D D , |
|||||
|
|
|
||||||||||||
|
A2 |
|
B2 |
C2 |
1 |
2 |
1 |
2 |
1 |
1 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|||||
107
- : |
A1 |
= |
B1 |
= |
C1 |
= 1 , |
|
- : A A + B B + C C |
2 |
= 0 . |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
A2 |
B2 |
C2 |
|
|
1 |
|
2 |
1 |
2 |
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задание { 10 }. |
Условие |
параллельности |
|
|
|
|
|
|
двух |
п |
||||||||||||||
A1 x + B1 y + C1 z + D1 = 0 и A2 x + B2 y + C2 z + D2 |
= 0 |
имеет вид: |
|
|||||||||||||||||||||
- : |
A1 |
= |
B1 |
= |
C1 |
= 1 , |
|
- : |
|
A1 |
= |
B1 |
= |
C1 |
, |
|
|
|
|
|||||
|
|
|
|
|
A2 |
|
|
|
|
|
|
|||||||||||||
|
A2 |
B2 |
C2 |
|
|
|
|
|
B2 |
|
C2 |
|
|
|
|
|
||||||||
- : A1 A2 + B1 B2 + C1C2 = D1D2 , |
- : A1 A2 + B1B2 + C1C2 = 0 . |
|
||||||||||||||||||||||
Задание { 11 }. |
Уравнение |
плоскости, |
проходящей |
через |
|
точкиA(2;3;1), |
||||||||||||||||||
B(3;1;4), C(2;1;5), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- : x + 2 y + z - 9 = 0 , |
|
- : x - 2 y - z + 9 = 0 , |
|
|
||||||||||||||||||||
- : x + 2 y + z + 9 = 0 , |
|
- : x - 2 y + z - 9 = 0 . |
|
|
||||||||||||||||||||
Задание { 12 }. |
Уравнение |
плоскости, |
проходящей |
через |
|
точки A(2;0;-1), |
||||||||||||||||||
B(- 2;4;1), C(0;2;-1), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : x + z - 2 = 0 , |
|
- : x - z + 9 = 0 , |
|
|
|
|
|
|||||||||||||||||
- : x + y - 2 = 0 , |
|
- : x - y + 9 = 0 . |
|
|
|
|
|
|||||||||||||||||
Задание { 13 }. Уравнение плоскости, проходящей через начало координат и |
||||||||||||||||||||||||
точки A(2;1;1), |
B(- 3;0;4), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- : 4x + 11y - 3z = 0 , |
|
- : 4x - 11y + 3z = 0 , |
|
|
||||||||||||||||||||
- : 4x + 11y + 3z = 1 , |
|
- : 4x + 11y + 3z = 0 . |
|
|
||||||||||||||||||||
Задание { 14 }. |
Уравнение |
плоскости, проходящей через точку A(3;5;-7) и |
||||||||||||||||||||||
отсекающей равные отрезки на осях координат, имеет вид: |
|
|
|
|
|
|||||||||||||||||||
- : x + y + z = 4 , |
|
- : x + y + z = 3 , |
|
|
|
|
|
|||||||||||||||||
- : x + y + z = 2 , |
|
- : x + y + z = 1 . |
|
|
|
|
|
|||||||||||||||||
Задание { 15 }. |
Уравнение плоскости, проходящей через точку A(1;1;2) и отсе- |
|||||||||||||||||||||||
кающей отрезки, равные 5 и –7 на осях Ох и Оу соответственно, имеет вид: |
|
|||||||||||||||||||||||
- : 14x - 10 y + 33z = 70 , |
|
- : 14x - 10 y + 33z = 50 , |
|
|||||||||||||||||||||
- : 14x - 10 y + 33z = 30 , |
|
- : 14x - 10 y + 33z = 10 . |
|
|||||||||||||||||||||
Задание { 16 }. |
Расстояние |
точки A(7;-1;2) |
|
|
|
|
|
|
от |
плоскости |
||||||||||||||
x + 2 y - 2z + 5 = 0 равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- : 1, |
|
|
|
|
|
|
|
- : 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
- : 3, |
|
|
|
|
|
|
|
- : 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задание { 17 }. |
Расстояние точки A(3;5;1) от плоскости x + 2 y - 2z + 5 = 0 |
|
||||||||||||||||||||||
равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
- : |
13 |
, |
|
|
|
|
|
- : |
|
16 |
, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
108
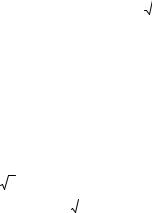
- : |
|
11 |
, |
|
|
|
|
|
|
|
|
|
- : |
|
19 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задание { 18 }. |
Расстояние точки A(2;0;4) от плоскости 2x - |
|
|
y + 3z = -4 |
||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||
равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- : 9, |
|
|
|
|
|
|
|
|
|
|
|
- : 7, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- : 5, |
|
|
|
|
|
|
|
|
|
|
|
- : 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задание { 19 }. |
Расстояние |
точки A(3;9;1) |
|
|
от |
плоскостиx - 2 y + 2z = 3 |
||||||||||||||||||||||||||||
равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- : |
|
4 |
, |
|
|
|
|
|
|
|
|
|
- : |
|
7 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- : |
|
11 |
, |
|
|
|
|
|
|
|
|
|
- : |
|
16 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Расстояние точки A( |
3;1;1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Задание { 20 }. |
|
от плоскости, проходящей через |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3;2;3), равно |
|||||||||||||||||
начало координат перпендикулярно вектору n = ( |
||||||||||||||||||||||||||||||||||
- : 2, |
|
|
|
|
|
|
|
|
|
|
|
- : 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- : 4, |
|
|
|
|
|
|
|
|
|
|
|
- : 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
точкиA(2;3;1), |
||||||||
Задание { 21 }. |
Уравнение |
прямой, |
проходящей |
через |
|
|||||||||||||||||||||||||||||
B(4;6;9), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
- : |
x - 2 |
= |
y - 3 |
= |
|
z - 1 |
, |
|
|
- : |
x + 2 |
= |
y + 3 |
= |
|
z + 1 |
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
6 |
9 |
10 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
8 |
|
|
|
|||||||||||
- : |
x - 2 |
= |
y - 3 |
= |
|
z - 1 |
, |
|
|
- : |
x + 2 |
= |
y + 3 |
= |
|
z + 1 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
3 |
8 |
|
|
|
|
|
6 |
|
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|||||||||||
Задание { 22 }. |
Уравнение |
прямой, |
проходящей |
|
|
через |
точкиA(7;-1;2), |
|||||||||||||||||||||||||||
B(5;1;4), имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
- : |
x - 7 |
= |
y + 1 |
= |
z - 2 |
, |
|
|
- : |
x + 7 |
= |
y - 1 |
= |
z + 2 |
, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
- 2 |
2 |
2 |
|
|
|
|
|
- 2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||||
- : |
x - 7 |
= |
y + 1 |
= |
z - 2 |
, |
|
|
- : |
x + 7 |
= |
y - 1 |
= |
z + 2 |
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
12 |
2 |
6 |
|
|
|
|
|
12 |
|
|
|
|
|
2 |
|
|
|
|
6 |
|
|
|
|||||||||||
Задание { 23 }. |
Уравнение |
прямой íìx - 2 y + 4z = 0, |
записанное в пара- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
î3x - 2 y + 5z = 0, |
|
|
|
|
|
||||||||||||||||
метрической форме, имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
- : x = t, y = 4t, z = 7t , |
|
|
- : x = 2t, y = -7t, z = 3t , |
|||||||||||||||||||||||||||||||
- : x = -t, y = 4t, z = -7t , |
|
|
- : x = -2t, y = 7t, z = 4t . |
|||||||||||||||||||||||||||||||
109
Задание { 24 }. |
|
|
|
Уравнение прямой íìx + y - z + 5 = 0, |
записанное в |
па- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î2x - y + 2z - 2 = 0, |
|
|
|
|
|
||||||||||||||||||||||||||
раметрической форме, имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
- : x = t, y = -4t, z = -3t , |
- : x = t, y = -8 - 4t, z = -3 - 3t , |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- : x = -t, y = -8t, z = -3t , |
- : x = 1 - 2t, y = 3 - 8t, z = -8 - 3t . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задание { 25 }. |
|
|
|
Направляющие |
косинусы cos a, cos b, cos g , |
прямой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x - 1 |
= |
|
y - 5 |
= |
|
z + 2 |
, соответственно равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
- 3 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
- : |
|
1 |
|
, |
4 |
|
|
, - |
|
5 |
|
, |
|
|
|
|
|
- : |
7 |
|
|
, |
|
9 |
|
|
, |
|
11 |
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
13 |
|
|
13 |
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
13 |
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
- : |
|
4 |
|
, - |
3 |
|
, |
|
12 |
, |
|
|
|
|
|
- : |
3 |
|
|
, |
|
4 |
|
|
, - |
|
5 |
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
13 |
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
13 |
|
13 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Задание { 26 }. |
|
|
|
Направляющие |
косинусы cos a, cos b, cos g , |
прямой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
= |
|
|
y - 7 |
= |
|
z + 3 |
, соответственно равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
12 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
- : |
12 |
, |
9 |
|
, |
20 |
, |
|
|
|
|
|
|
|
|
- : |
3 |
|
|
|
, |
5 |
|
|
, |
|
7 |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
25 |
25 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
25 |
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
- : |
4 |
|
, - |
3 |
|
|
, |
12 |
, |
|
|
|
- : |
7 |
|
|
|
, |
3 |
|
|
, |
|
16 |
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
25 |
25 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
25 |
|
25 |
25 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Задание { 27 }. |
|
|
|
Направляющие |
косинусы cos a, cos b, cos g , |
прямой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ì5x - 6 y + 2z + 21 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соответственно равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
îx - z + 3 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
- : |
6 |
|
, |
7 |
, |
6 |
, |
|
|
|
|
|
|
|
|
- : |
6 |
|
, |
7 |
|
, |
6 |
, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
25 |
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
- : |
6 |
|
, - |
7 |
, - |
6 |
, |
|
|
- : - |
6 |
, |
7 |
|
, |
6 |
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
31 |
31 |
31 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Задание { 28 }. |
|
|
|
Косинус угла |
между прямыми |
x - 1 |
= |
y + 2 |
= |
z - 5 |
|
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
y - 3 |
|
|
|
|
|
|
z + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
= |
|
= |
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
73 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|||||||||||||||||
- : cos j = ± |
, |
- : cos j = ± |
, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
||||||||||||
- : cos j = ± |
72 |
, |
- : cos j = ± |
71 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
||||||||||||
110

Задание { 29 }. |
Косинус |
угла |
между |
прямыми |
x + 2 |
= |
|
y + 4 |
|
= |
z + |
8 |
и |
|||||||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x - 1 |
|
y - 3 |
|
|
|
|
|
|
|
z |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
11 |
|
||||||||||||
|
= |
= |
|
|
|
|
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5 |
0 |
11 |
|
|
11 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
- : cos j = ± |
, |
|
|
|
|
|
|
|
|
- : cos j = ± |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : cos j = ± |
11 |
, |
|
|
|
|
|
|
|
|
- : cos j = ± |
11 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
25 |
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Задание { 30 }. |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y - 1 |
|
|
|
z - 1 |
|
|
|
||||||||||||||
Угол |
образованный |
прямыми |
= |
|
|
|
= |
|
|
|
|
|
, |
|
и |
|||||||||||||||||||||||
1 |
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||
|
x - 1 |
|
y - 1 |
|
|
|
|
|
z |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= |
= |
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
1 |
|
|
|
|
|
0 |
|
|
|
|
|
- : 300, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- : 600, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- : 450, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- : 900. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГЛАВА 5. ВВЕДЕНИЕ В АНАЛИЗ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§1. Понятие функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Пусть даны два непустых множества X |
и Y . Переменная |
|
y называ- |
||||||||||||||||||||||||||||||||
ется однозначной функцией f |
от переменной x в данной области измене- |
|||||||||||||||||||||||||||||||||||||
ния |
X = {x}, если каждому значению x Î X |
ставится в соответствие одно |
||||||||||||||||||||||||||||||||||||
определенное действительное значение y = f (x), принадлежащее множеству Y = {y}. Говорят также, что функция f отображает множество X на множество Y . При этом, переменная x называется аргументом или незави-
симой переменной, а у – функцией или зависимой переменной. Функция,
все значения которой равны между собой, называется постоянной. Множество X носит названиеобласти определения или области
существования функции f (x), а Y – множеством значений этой функ-
ции.
В простейших случаях множество X представляет собой или откры-
тый интервал: (a; b), a < x < b или полуоткрытые интервалы: (a; b],
a < x £ b ; [a; b), a £ x < b |
или замкнутый интервал (отрезок или сег- |
мент): [a; b], a £ x £ b , где |
a и b – некоторые вещественные числа или |
символы -¥ и +¥ (в последних случаях равенства исключаются).
Пример 1. Администрация планирует организовать торговлю определенным видом товара. Опрос продавцов и покупателей показал, что функция
111
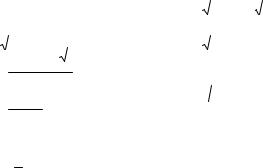
предложения |
на товар имеет |
вид: Q = 0.5 × 2P + 84 , а функция |
спроса– |
Q = -0.5 × 2P |
+ 116 . Здесь, Q |
– дневной объем продаж (шт.); P |
– цена |
единицы товара (руб/шт). Найти: 1) множество значений функции предложения на интервале цен [1; 6] руб/шт; 2) значение функции спроса при цене
на товар P = 2 руб/шт.; 3) объем продаж при равновесной цене.
Решение: 1) Подставляя значения P = 1 и P = 6 в функцию предложения, получим Q(1) = 85 , Q(6) = 116 . Таким образом, ответ на первый вопрос задачи имеет вид: [85;116].
2) Для ответа на второй вопрос задачи достаточно подставить значение P = 2 в функцию спроса: Q(2) = -0.5 × 22 + 116 = 114 шт.
3) Прежде чем найти объем продаж, необходимо установить равновесную цену товара. Приравнивая правые части функций спроса и предложения, находим P = 5 руб/шт. Теперь, подставляя найденное значение равновесной цены, например в функцию предложения, получим расчетный объ-
ем продаж: Q(5) = 0.5 × 25 + 84 = 100 шт.
Задания.
471.Вычислить f (0), f (1), f (2), f (3), если f (x) = x4 - 6x3 + 11x2 - 6x .
472.Вычислить f (- 1), f (- 0.001), f (100), если f (x) = lg x2 .
473. Вычислить f (0.9), f (0.99), f (0.999), f (1), если f (x) = 1 + [x], где
[x] – целая часть числа x .
Найти области определения (существования) следующих функций:
474. |
y = 3x + 3 . |
|
|
|
475. |
y = x2 + 5x - 6 . |
|||||||||||
476. |
y = |
3x - 1 |
. |
|
|
|
|
477. |
y = |
|
+ |
|
. |
||||
|
|
|
|
x - 1 |
1 - x |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
5x + 6 |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
478. |
y = 3x - 1 + |
|
|
. |
479. |
y = |
2 - 3x + lg x . |
||||||||||
|
|
|
|||||||||||||||
4 - x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
480. y = 
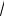 x2 - 4x + 3 .
x2 - 4x + 3 .
482. y = 
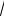 1 - x2 . 484. y = x + cos x .
1 - x2 . 484. y = x + cos x .
486. y = tg x .
2
488. y = log2 (2x - 1).
1
481. y =  .
.  x2 - 4x
x2 - 4x
483. y = sin 4x .
485. y = ctg x .
487. y = arctg(2x - 1).
489. y = log2 (log3 x).
112
490. |
y = log5 (3x - x2 ). |
|
|
491. |
y = |
1 |
|
|
. |
|
|
|||||||||||||
|
|
log2 (1 - 2x) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
- |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
492. |
y = |
|
|
|
|
. |
|
|
493. |
y = 2 x . |
|
|
|
|
|
|||||||||
x2 - 5x + 4 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
494. |
Построить |
области изменения переменной x , удовлетворяющей |
||||||||||||||||||||||
неравенствам: 1) |
| x |< 4 ; |
2) x2 £ 9 ; |
3) |
| x - 4 |< 1 ; 4) |
-1 < x - 3 £ 2 ; |
|||||||||||||||||||
5) x2 > 9 ; 6) (x - 2)2 £ 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
495. |
Записать неравенствами и построить интервалы изменения пере- |
|||||||||||||||||||||||
менных: 1) [-1, 3]; |
2) (0, 4); 3) [-2, 1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
496. |
Определить область изменения переменной x = 1 - |
, где t при- |
||||||||||||||||||||||
|
||||||||||||||||||||||||
нимает любое значение ³ 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |£ 3 графики |
||||||||||||
В задачах 497-499 построить по |
точкам на отрезке| |
|||||||||||||||||||||||
указанных функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
497. |
1) y = 2x ; |
2) |
y = 2x + 2 ; |
3) y = 2x - 2 . |
|
|
|
|
|
|||||||||||||||
498. |
1) y = x2 ; |
2) |
y = x2 |
+ 1; |
3) y = x2 |
- 1 . |
|
|
|
|
|
|||||||||||||
|
1) y = |
x3 |
|
y = |
x3 |
|
|
y = |
x3 |
|
|
|
|
|
|
|
|
|
||||||
499. |
|
; |
2) |
|
+ 1 ; |
3) |
|
|
|
- 1 . |
|
|
|
|
|
|||||||||
3 |
3 |
3 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
500. Построить графики функций: 1) |
y = |
6 |
; 2) y = 2x ; 3) y = log2 x . |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
Какую особенность в расположении этих кривых относительно осей координат можно заметить?
501. Построить на одном |
чертеже графики функций: 1) y = sin x ; |
2) y = cos x по точкам, в которых |
y имеет наибольшее, наименьшее и нуле- |
вое значения. Сложением ординат этих кривых построить на том же чертеже график функции y = sin x + cos x .
502. Найти корни x1 и x2 функции y = 4x - x2 и построить ее график на отрезке [x1 - 1, x2 + 1] .
503. Построить графики функций: 1) y =| x | ; 2) y = - | x - 2 | ;
3)y =| x | -x .
Взадачах 504-507 найти области определения вещественных значений функций и построить их графики.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
504. 1) |
y = |
x + 2 ; |
|
2) y = |
|
9 - x2 ; |
3) y = 4x - x2 . |
|||||||
505. 1) |
y = |
|
+ |
|
; |
2) y = arcsin |
x - 1 |
. |
||||||
- x |
4 + x |
|||||||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
113

506. |
1) |
y = |
x (2 ± x ) |
; |
2) |
y = ± x |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 - x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = - |
|
x 16 - x2 |
|
|
|
|
|
|
|
|
|
||||||||||
507. |
1) |
y = - |
|
2 sin x ; |
2) |
|
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
508. l) |
f (x) = x2 - x + 1; вычислить f (0), f (l), f (–l), f (2), f (a+1); |
|
|
|||||||||||||||||||||||||||||
2) j(x) |
|
2x - 3 |
|
|
|
|
|
|
|
æ |
3 ö |
æ 1 |
ö |
|
1 |
|
. |
|
|
|||||||||||||
= |
|
|
|
|
; вычислить j(0), j(-1), jç |
|
|
|
÷, jç |
|
÷, |
|
|
|
|
|||||||||||||||||
x2 + 1 |
2 |
|
|
j(x) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
è x |
ø |
|
|
|
|
|
|||||||||||||
|
F (x) = x |
2 |
|
|
|
|
F (b) - F (a) |
|
|
|
|
|
æ a + h ö |
æ a - h ö |
||||||||||||||||||
509. |
|
; вычислить: 1) |
|
|
|
|
; 2) |
|
|
Fç |
|
|
|
|
|
÷ |
- Fç |
|
|
|
÷ . |
|||||||||||
|
b - a |
|
|
2 |
|
|
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
è |
|
|
ø |
|||||||||||||
510. |
f (x) = x2 , j(x) = x2 ; вычислить |
|
f (b) - f (a) |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j(b) - j(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
511.F (x, y) = x3 - 3xy - y2 , вычислить F(4, 3) и F(3, 4).
512.Функция f (x) называется четной, если f (-x) = f (x) ; нечетной, если f (-x) = - f (x) . Указать, какие из следующих функций четные и какие нечетные:
1) |
f (x) = |
sin x |
; |
|
2) |
j(x) = |
a x |
- 1 |
; |
3) |
F (x) = a x + |
1 |
; |
|
|
|
a x |
+ 1 |
a x |
||||||||||
|
|
x |
|
|
|
|
|
|
|
|||||
4) |
F(x) = a x - |
1 |
; |
5) |
Y(x) = x sin 2 |
x - x2 ; |
6) |
f (x) = x + x2 . |
|
|||||
a x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
513. Середина любой хорды графика некоторой функции f (x) лежит выше графика этой функции. Записать это свойство функции неравенством. Проверить, что этим свойством обладает функция f (x) = x2 .
514. |
Какая из элементарных функций обладает |
свойствамиf (1) = 0 , |
|||
f (a) = 1 , f (xy) = f (x) + f ( y) ? |
свойствамиf (0) = 1 , |
||||
515. |
Какая из элементарных функций обладает |
||||
f (1) = a , f (x + y) = f (x) f ( y) ? |
|
|
|
||
516. |
Построить области изменения переменной x , удовлетворяющей |
||||
неравенствам: |
|
|
|
||
1) | x |< 3 ; 2) x2 £ 4 ; 3) | x - 2 |< 2 ; 4) (x - 1)2 £ 4 . |
|||||
517. |
Определить область изменения переменной x = 2 + |
1 |
, где t при- |
||
|
|||||
нимает любое значение ³ 1 . |
|
t |
|||
|
|
|
|||
518. Построить графики функций: |
|
|
|
||
|
x3 |
|
|
|
|
1) y = 4 - |
|
на отрезке | x |£ 2 ; |
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
114

2) y = 3,5 + 3x - x2 между точками пересечения с осью абсцисс.
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
519. |
Построить графики функций: |
|
|
|
|
|
|
|
|
|
|||||||||||||
1) |
y = x - 4 + |
|
|
x - 2 |
|
на отрезке [-2, 5]; |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2) |
y = 1 - cos x на отрезке | x |£ 2p . |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
520. |
Построить графики функций: 1) |
y = - |
4 |
|
; 2) y = 2-x . |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
521. |
Найти области определения вещественных значений функций: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) |
y = 4 - x2 ; |
2) y = |
|
|
|
- |
|
|
; |
|||||||||||||||
x + 1 |
3 - x |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
3) |
y = 1 - |
|
2 cos 2x ; |
4) y = |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
и построить их графики, |
1 + |
|
x2 - 4 |
|||||||||||||||||||||
|
2x + 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
522. |
1) Для функции |
f (x) = |
|
вычислить f (0), f (–2), f (–1/2), |
|||||||||||||||||||
|
x2 + 1 |
|||||||||||||||||||||||
f (x - 1), f (1/2); |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2) |
для функции j(x) = x3 вычислить |
j(x + h) - j(x - h) |
; |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
||||||
3) |
для функции f (x) = 4x - x2 вычислить |
f (a + 1) - f (a - 1) . |
||||||||||||||||||||||
§2. Пределы последовательности и функции. Бесконечно малые и бесконечно большие.
Пусть каждому натуральному числу n = 1, 2, 3, K по некоторому зако-
ну поставлено в соответствие число xn . Тогда говорят, что этим определена
числовая последовательность x1 , x2 , x3 ,… Кратко последовательность обозначается в виде {xn } = {x1 , x2 , x3 ,...} или xn , n Î N . Отдельные числа последовательности {xn } называются ее элементами. Говорят еще, что переменная xn пробегает значение последовательности {xn } .
Число A называется пределом последовательности {xn } , если для любого e > 0 найдется такое натуральное числоN , что для всех n > N выполняется неравенство xn - A < e .
Если последовательность {xn |
} имеет предел A , то пишут lim xn = A |
|
n ®¥ |
или xn ® A . В этом случае, последовательность называется сходящейся.
115

Если, в случае числовой последовательности{xn }, существует такое |
||||||
число M > 0 , что для " n Î N выполняется неравенство |
|
xn |
|
£ M , то такую |
||
|
|
|||||
последовательность называют ограниченной. |
|
|
|
|
|
|
Последовательность {xn } |
называется бесконечно |
|
малой, |
если |
||
lim xn = 0 . |
|
|
|
|
|
|
n ®¥ |
|
|
|
|
|
|
Последовательность {xn } |
называется бесконечно |
большой, если |
для |
|||
любого M > 0 существует такое натуральное число N (M ), |
|
что для любого |
||||
n > N верно неравенство xn > M . Для бесконечно большой последователь-
ности пишут lim xn = ¥ и говорят, что ее пределом является бесконечность.
n ®¥
Перейдем к определению предела функции. Пусть функция y = f (x) определена в некоторой окрестности точкиx0 , кроме, быть может, самой
точки x0 .
Существует два эквивалентных определения
(по Гейне): Число A называется пределом функции y = f (x) в точ-
ке |
x0 , если для любой последовательности допустимых значений аргумента |
|||||||||||
xn , |
n Î N (xn ¹ x0 ), |
сходящейся к x0 , последовательность соответствую- |
||||||||||
щих значений функции |
f (xn ), n Î N , сходится к числу A ; |
|||||||||||
|
(по Коши): Число A называется пределом функции y = f (x) в точ- |
|||||||||||
ке |
x0 , если для любого числа e > 0 |
существует такое числоd (e ) > 0 , что |
||||||||||
при всех x ¹ x0 , удовлетворяющих |
условию |
|
x - x0 |
|
< d , выполнено нера- |
|||||||
|
|
|||||||||||
венство |
|
f (x) - A |
|
< e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Если число A является пределом функции f (x) |
в точке x0 , то пишут |
||||||||||
lim f (x) = A или f (x) ® A при x ® x0 . |
|
|||||||||||
x ® x0 |
|
|
|
|
|
|
|
|||||
|
В определении предела функции считается, что |
x стремится к x0 лю- |
||||||||||
бым способом. Но бывают случаи, когда способ приближения аргумента x к точке x0 существенно влияет на значение предела. Поэтому вводят следующие понятия.
Число A называется пределом функции y = f (x) слева в точке x0 , если для любого числа e > 0 существует такое число d (e ) > 0 , что при всех
x Î (x0 - d; x0 ) |
выполнено неравенство |
|
f (x) - A |
|
< e . Предел слева обозна- |
|
|
||||
чают через lim |
f (x). |
|
|
|
|
x ® x0 - 0
116

Число A называется пределом функции y = f (x) справа в точке x0 , если для любого числа e > 0 существует такое число d (e ) > 0 , что при всех x Î (x0 ; x0 + d ) выполнено неравенство f (x) - A < e . Предел справа обо-
значают через lim f (x).
x ® x0 + 0
Пределы функции слева и справа называютсяодносторонними пре-
делами.
Функция y = f (x) имеет предел в точке x0 тогда и только тогда, ко-
гда существуют оба односторонних предела и они равны.
Понятия бесконечно малых и бесконечно больших функций вводятся аналогично понятиям для последовательностей.
В заключении следует отметить, что понятие предела в математике тесно связано с различными понятиями в экономике. Приведем пока лишь два примера из микроэкономики: 1) Предельный доход (marginal revenue – MR) – приращение дохода, которое возникает за счет бесконечно малого увеличения выпуска продукции; причем, если MR=P, где P – цена, то в условиях совершенной конкуренции это означает, что эластичность спроса по цене бесконечно велика. 2) Предельные издержки (marginal cost – MС) – приращение совокупных издержек, вызванное бесконечно малым увеличением производства.
Задания.
523. Полагая n = 1, 2, 3, K, написать последовательности значений переменных:
|
1 |
|
1 |
æ |
|
1 |
ön |
|
a = |
|
, a = - |
|
, a = ç |
- |
|
÷ . |
|
2n |
2n |
2 |
||||||
|
|
è |
|
ø |
Начиная с какого n модуль каждой из переменной сделается и будет
оставаться меньше 0,001, меньше данного положительного e ? |
|
||||||
524. |
|
Написать |
последовательность |
значений |
переменно |
||
x = 1 + |
(-1)n |
|
. Начиная с какого n модуль разности x - 1 станет и будет |
||||
2n + 1 |
|||||||
|
|
|
|
|
|||
оставаться меньше 0,01, меньше данного положительного e ?
525.Прибавляя к 3 (или вычитая из 3) сначала 1, затем 0,1, потом 0,01
ит.д. записать «десятичными» последовательностями приближения пере-
менной к пределу: xn ® 3 + 0 , xn ® 3 - 0 .
117
526. Записать «десятичными» последовательностями приближения переменных к пределам: xn ® 5 + 0 ; xn ® 5 - 0 ; xn ® -2 + 0 ; xn ® -2 - 0 ; xn ® -1 + 0 ; xn ® -1 - 0 ; xn ® -1, 2 + 0 ; xn ® -1, 2 - 0 .
527. Доказать, что lim x2 = 4 . Пояснить таблицами значений x и x2 .
x ®2
528. |
Доказать, |
что |
lim (2x - 1) = 5 . По данному числу e > 0 найти |
||
|
|
|
x ®3 |
|
|
наибольшее число d |
> 0 такое, чтобы при любом x |
из d -окрестности числа |
|||
3 значение |
функции |
y = 2x - 1 оказалось в e -окрестности |
числа 5. Пояс- |
||
нить графически. |
|
|
|
|
|
529. |
Доказать, |
что |
lim (3 - 2x - x2 ) = 4 . Из |
какой |
наибольшей d - |
|
|
|
x ®-1 |
|
|
окрестности числа -1 нужно взять значение x , чтобы значение функции
y= 3 - 2x - x2 отличалось от ее предела меньше чем на e = 0, 0001 ?
530.Доказать, что sin a , есть бесконечно малая при a ® 0 .
Указание. Построить чертеж и показать, что | sin a |<| a | .
|
|
531. |
Доказать, что lim |
sin x = sin a . |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Указание. Положив |
x = a + a , |
составить разность sin x - sin a и |
||||||||||||||||||||||||||
затем положить a ® 0 . |
|
|
3x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
532. |
Доказать, что |
lim |
|
|
= 3 . Пояснить таблицами значений x |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
3x + 4 |
|
|
|
|
|
|
|
|
|
x ®¥ |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
, при x=1, 10, 100, 1000,... |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x - 3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
533. |
Доказать, что |
lim |
|
|
|
= 2 . При каких x |
значения функции |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®¥ |
|
|
2x + 1 |
|
|
|
|
|
|
|
|
||||||
будут отличаться от своего предела меньше чем на 0,001? |
|
|
|
|
|||||||||||||||||||||||||||
|
|
534. |
Доказать, что |
lim |
|
1 - 2x2 |
|
= -0,5 . При каких x значения функ- |
|||||||||||||||||||||||
|
|
|
2 + 4x2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®¥ |
|
|
|
|
|
|
|
|
|
||||||||
ции будут отличаться от своего предела меньше чем на 0,01? |
|
|
|
||||||||||||||||||||||||||||
|
|
535. |
|
Доказать, |
что |
lim0,333...3 = |
1 |
, |
составив |
разности |
1 |
- 0,3 ; |
|||||||||||||||||||
|
|
|
3 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ®¥14243 |
|
|
|
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n знаков |
|
|
|
|
|
|
|
|
|||||
1 |
- 0,33 ; |
1 |
- 0,333 |
1 |
; |
1 |
- 0,333...3 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
3 |
|
|
3 |
3 |
|
14243 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
n знаков |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
536. |
Написать последовательности: |
|
|
|
|
|
|
|
|||||||||||||||||||||
1) |
xn = |
|
n |
|
|
; |
|
|
|
2) xn |
= - |
|
n |
; |
|
|
3) xn = |
(-1)n n |
; |
|
|
||||||||||
|
|
|
|
|
|
|
|
n + 1 |
|
|
n + 1 |
|
|
||||||||||||||||||
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
118
|
|
|
|
8 cos n |
p |
|
|
|
|
|
|
|
|
|
2n + (-1)n |
|
|
|
|
|
|
||||||||||
4) xn |
= |
2 |
|
; |
|
5) |
|
xn |
= |
|
; |
6) |
xn = 2-n a cos pn . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
n + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
|
|
|
Существует ли |
lim |
xn |
в каждом примере и чему он равен? |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n ®+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
537. |
Найти |
lim |
3 |
|
|
|
|
и lim |
|
|
3 |
и пояснить таблицами. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
n ®2 +0 x - 2 |
n ®2 -0 x - 2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
538. |
Найти |
lim |
21 / x |
|
и |
lim 21 / x |
и пояснить таблицами. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
n ®0 +0 |
|
|
|
|
n ®0 -0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
539. |
Выяснить точный смысл «условных» записей: |
|
|
|
||||||||||||||||||||||||
1) |
2 |
= 0 ; |
|
|
|
|
|
2) |
2 |
= ±¥ ; |
|
|
|
|
|
3) 3¥ = ¥ ; |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
¥ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) 3-¥ |
= 0 ; |
|
|
|
|
|
5) lg 0 = -¥ ; |
|
|
6) tg90o = ±¥ . |
|||||||||||||||||||||
|
|
|
540. |
Показать, что lim |
sin x не |
существует, составив |
последователь- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n ®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ности значений sin x : |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
p |
|
|||||||||||
1) при x = np ; |
|
|
2) при x = |
+ 2pn ; |
3) |
при |
x = - |
+ 2pn , |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
( n = 0,1, 2, 3, 4, ... ). |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
541. |
Показать, что lim sin |
1 |
не существует. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x ®0 |
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
542. |
Показать, что lim |
x sin |
1 |
= 0 |
при |
любом способе приближения |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
x к 0. |
|
|
|
|
|
|
|
x ®0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
радиусаR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
543. |
В круг |
вписан |
правильный |
многоугольник с числом |
||||||||||||||||||||||||
сторон n и стороной а. Описав около круга квадрат, показать, что an < e , как только n > 8R / e , т.е. an ® 0 , когда n ® ¥ .
544. Пусть |
rn - апофема правильного, вписанного в круг n-угольника. |
Доказать, что lim |
rn = R , где R - радиус круга. |
n ®¥ |
|
545.Вершина В треугольника АВС перемещается по прямойВЕ||АС, неограниченно удаляясь вправо. Как будут при этом изменяться стороны треугольника, его площадь, внутренние углы и внешний угол BCD?
546.Написать «десятичные» последовательности приближений пере-
менных |
к |
пределам: xn ® 4 + 0 ; |
xn ® 4 - 0 ; |
xn ® -1, 5 + 0 ; |
xn ® -1, 5 - 0 . |
|
|
|
|
547. Доказать, что: 1) lim x3 = 27 ; |
2) lim(x2 + 2x) = 3 . |
|||
|
|
x ®3 |
x ®1 |
|
119

548. Доказать, что lim |
5x + |
2 |
|
|
|
x ®¥ 2x |
|
|
5x + 2 - 2, 5 есть бесконечно малая при
2x
таблицей, полагая x= 1, 10, 100, 1000, ...
549. Доказать, что lim cos x = cos a
x ®a
= 2, 5 , показав, что |
разность |
x бесконечно большом. Пояснить
(cм. задачу 530).
550. Написать последовательности значений переменных:
1) x |
|
|
|
|
æ |
|
1 ön |
|
|
|
|
|
|
|
|
|
2) x |
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
= 1 + ç- |
|
|
|
÷ ; |
|
|
|
|
|
|
|
|
|
n |
= |
(-1) |
|
+ |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n sin |
np |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3) xn = (-1)n (2n + 1) ; |
|
|
|
|
|
|
|
|
4) xn = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Какая из последовательностей имеет предел при n ® +¥ ? |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
551. Найти: |
1) |
lim |
|
|
1 |
|
; |
2) |
|
|
lim |
1 |
|
|
; 3) |
|
lim |
3tg 2 x ; 4) |
lim 3tg 2 x ; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®1-0 2x -1 |
|
|
|
|
x ®1+0 2x -1 |
|
|
|
|
|
|
|
x ® |
p |
-0 |
|
x ® |
p |
+0 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
4 |
|
|
|
|
4 |
|
|
|
|
||||||
5) lim |
|
|
|
|
|
; |
6) |
lim |
|
|
|
|
|
|
; |
|
7) |
|
lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x ® |
p |
+0 1 + 2tg 2 x |
|
|
|
x ® |
p |
-0 1 + 2tg 2 x |
|
|
|
|
|
x ®+¥ 1 + a x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
552. |
Доказать, |
что |
lim0,666...6 = |
2 |
, |
|
|
составив |
разности |
2 |
- 0,6 ; |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ®¥14243 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n знаков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
- 0,66 ;…; |
2 |
- 0,666..6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
14243 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n знаков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
553. Пусть an - внутренний угол правильногоn-угольника. Доказать, |
||||||||||||||||||||||||||||||||||||||||||||||||||
что lim an |
= p . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n ®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
справа взята точкаМ на рас- |
||||||||||||||||||||||
|
|
|
|
|
554. На продолжении |
отрезка |
|
|
AB = a |
|
|
||||||||||||||||||||||||||||||||||||||||||||
стоянии BM = x . Найти lim |
AM |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ® ¥ BM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
§ 3. Свойства пределов. Раскрытие неопределенностей вида |
0 |
|
и |
¥ |
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
¥ |
|
||||||
|
|
|
|
|
Пусть все данные величины(слагаемые, сомножители, делимое и де- |
||||||||||||||||||||||||||||||||||||||||||||||||||
литель) зависят от одного |
аргумента x |
|
и обладают конечными |
пределами |
|||||||||||||||||||||||||||||||||||||||||||||||||||
(при |
|
x ® x0 |
|
или |
при x ® ¥ ). |
Тогда, |
основные |
свойства пределов могут |
|||||||||||||||||||||||||||||||||||||||||||||||
быть представлены равенствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1) lim c = c , ( c - const ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
120
|
2) |
|
lim [ |
f (x) ± g(x)] = lim f (x) ± lim g(x); |
|
|
|
|
|||||||||||||||||||||
|
3) |
|
lim [c × |
f (x)× g(x)] = c × lim f (x)× lim g(x); |
|
|
|||||||||||||||||||||||
|
4) |
|
lim [ |
f (x)]n = [ lim f (x) ]n ; |
|
|
|
|
|
|
|||||||||||||||||||
|
5) |
|
lim |
f (x) |
|
= |
|
lim f (x) |
, ( lim g(x) ¹ 0 ); |
|
|
|
|
|
|||||||||||||||
|
|
g(x ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim g(x ) |
|
|
|
|
|
|
|
|
||||||||||||
|
6) |
|
Если для всех значений x |
в некоторой окрестности точки x0 , кро- |
|||||||||||||||||||||||||
ме, быть может, |
x = x0 , функции |
f (x) и j(x) |
|
равны и одна из них имеет |
|||||||||||||||||||||||||
предел при x ® x0 , то и вторая имеет тот же предел. |
|
|
|||||||||||||||||||||||||||
|
Последнее |
|
|
свойство |
применяется при |
раскрытии |
неопределенностей |
||||||||||||||||||||||
|
0 |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
x2 |
|
- a 2 |
|
|
|
|
|
|
|
|
||||
вида |
|
|
и |
|
|
. Например, |
|
|
|
|
|
= x + a |
при любых x , кроме x = a . Сле- |
||||||||||||||||
0 |
|
¥ |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x - a |
|
|
|
|
|
|
|
|
||||||||
довательно, согласно свойству lim |
|
x2 - a2 |
|
= lim (x + a) = 2a . |
|||||||||||||||||||||||||
|
x - a |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®a |
x®a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания. |
|
|
|
|
|
|
|||
|
Найти пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
555. 1) lim |
x2 - 4x + 1 |
; |
|
|
2) |
lim |
|
|
1 + sin 2x |
. |
|
|||||||||||||||||
|
|
|
2x + 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
x ®2 |
|
|
|
|
|
|
|
|
|
|
|
x ®p / 4 1 - cos 4x |
|
|
||||||||
|
556. lim |
x2 |
- 4 |
|
|
(пояснить таблицей). |
|
|
|
|
|
|
|||||||||||||||||
|
x - 2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
x ®2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
557. lim |
|
|
x - 2 |
|
. |
|
|
|
|
|
558. lim |
|
x2 - 9 |
|
. |
|||||||||||||
|
|
|
- 3x + 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x ®2 x2 |
|
|
|
|
|
|
|
|
|
|
x ®3 x2 - 2x - 3 |
|||||||||||||
Указание. Решить пример 557 двумя способами: 1) полагая x = 2 + a ; 2) разлагая знаменатель на множители.
559. lim tg x . x ®p sin 2x
x
561. lim  . x ®0
. x ®0  1 + 3x - 1
1 + 3x - 1
563.lim 3  x - 1 .
x - 1 .
x®1 
 x - 1
x - 1
560. lim |
sin x - cos x |
. |
|
||
x ®p / 4 |
cos 2x |
|
562.lim 
 ax - x .
ax - x .
x ®a x - a
564. lim 3  1 + mx - 1 .
1 + mx - 1 .
x ®0 x
Указание. В примере 563 положить x = t 6 , а в примере564
1 + mx = t 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
. |
565. lim |
|
1 + x |
- |
1 - x |
|
. |
566. lim |
1 - tg x |
1 + tg x |
||||
|
|
|
|
|
|
|
|
|
|
||||
x ®0 |
|
|
x |
x ®p |
|
sin 2x |
|||||||
121

567. 1) lim |
2x |
2 - 1 |
; |
2) lim |
5x3 - 7x |
. |
|||||
|
|
- 4x |
|
|
|
|
|||||
x ®¥ 3x2 |
|
|
x ®¥ 1 - 2x3 |
|
|||||||
Указание. Можно решить двумя способами: 1) разделив числитель и |
|||||||||||
знаменатель на x |
в высшей степени; 2) положив x = 1 / a . |
||||||||||
568. lim |
3x - 1 |
|
. |
|
569. lim |
x3 |
- 1 |
|
. |
||
|
+ 1 |
|
|
+ 1 |
|||||||
x ®¥ x2 |
|
|
x ®¥ x2 |
|
|||||||
570.lim 
 x - 6x .
x - 6x .
x ®¥ 3x + 1
572. lim 
 2n2 + 1 .
2n2 + 1 .
n ®¥ 2n - 1
Найти пределы:
574.lim 3x + 6 .
x®-2 x3 + 8
576. |
lim |
x2 |
- x - 2 |
. |
|
|
x3 |
+ 1 |
|||
|
x ® -1 |
|
|
||
578.lim 5x2 - 3x + 2 .
x® ¥ 2x2 + 4x + 1
|
|
æ |
5x2 |
|
1 |
ö |
|||||
|
|
|
|
|
|
|
|||||
580. |
lim |
ç |
|
|
|
|
+ 2 x |
÷ . |
|||
|
|
|
2 |
||||||||
|
x ® ¥ç |
1 - x |
|
|
|
|
÷ |
||||
|
|
è |
|
|
|
|
|
ø |
|||
|
lim |
2 - |
|
|
|
. |
|
||||
582. |
|
x - 3 |
|
||||||||
|
- 49 |
|
|
||||||||
|
x ®7 |
|
x2 |
|
|
|
|
||||
571. |
lim |
|
|
|
3n |
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n ®¥ 1 - 2n |
|
|
|
|
|
|
|
||||||||||||
573. |
lim |
1 + 2 |
+ 3 + ... |
+ n |
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n ®¥ |
|
|
|
|
|
9n4 + 1 |
|||||||||||||
575. |
|
|
|
|
9 - x2 |
|
|
|
|
|
|
|
||||||||
lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x ®3 |
|
3x - 3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
577. |
lim |
|
|
|
1 + cos x |
|||||||||||||||
|
|
|
|
sin x |
|
|
||||||||||||||
|
x ®p +0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
579. |
lim |
|
|
3n |
+ 1 |
|
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n ®¥ |
|
|
3n2 + 1 |
|
|
|
|
|
|
|
|||||||||
581. |
lim |
1 + 3 + 5 + ... + (2n - 1) |
. |
|||||||||||||||||
|
|
|||||||||||||||||||
|
n ® ¥ |
|
|
1 + 2 + 3 + ... + n |
||||||||||||||||
583. |
lim |
|
|
sin 2x - cos 2x - 1 |
. |
|||||||||||||||
|
|
|
||||||||||||||||||
|
x ®p / 4 |
|
|
|
cos x - sin x |
|||||||||||||||
§ 4. Первый замечательный предел.
При раскрытии неопределенностей вида 0 , а также при нахождении
0
пределов содержащих тригонометрические функции, часто используют равенство
lim |
sin x |
= lim |
x |
= 1 , |
|
|
|||
x ®0 x |
x ®0 sin x |
|||
называемое первым замечательным пределом.
Задания.
Найти пределы:
122
584. |
lim |
|
sin 4x |
|
|
|
(умножить и разделить на 4 или положить 4x = a ). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x ®0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
tg x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
585. |
lim |
|
|
3 |
. |
|
|
|
|
586. |
lim |
|
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x ® 0 |
x |
|
|
|
x ®0 |
|
|
x |
|||||||||||||||||
|
|
|
sin 2 |
x |
|
|
|
|
|
|
|
|
|
|
1 - cos 2x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
587. |
lim |
|
|
3 |
. |
|
|
|
588. |
lim |
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
x ®0 |
x2 |
|
|
|
x ® 0 |
|
|
x sin x |
|||||||||||||||||
589. |
lim |
|
|
|
|
sin 3x |
|
. |
590. |
lim |
sin(x + h) - sin(x - h) |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x ®0 |
x + 2 - |
2 |
|
|
h ®0 |
|
|
|
|
h |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
591. 1) lim |
arctg x |
; |
|
|
2) lim |
arcsin (1 - 2x) |
. |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
x ®0 |
|
|
|
|
|
x |
|
|
x ®1 / 2 |
|
|
4x2 - 1 |
|||||||||||||
Указание. |
|
Положить в |
примере1) |
arctg x = a , а в примере2) |
||||||||||||||||||||||
arcsin (1 - 2x) = a .
592.lim 1 - cos x .
x ®0 x2
Найти пределы:
594. |
lim |
|
|
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x ® 0 sin 3x |
|
|
|
||||||||
596. |
lim |
|
1 - cos 2x |
|
. |
|||||||
|
|
|
x |
|
|
|||||||
|
x ®-0 |
|
|
|
|
|
||||||
598. |
lim |
1 - cos mx |
. |
|||||||||
|
|
|||||||||||
|
x ®0 |
x2 |
|
|
|
|||||||
|
ésin(x - 2) |
|
|
|
||||||||
600. |
limê |
|
|
|
|
|
+ 2 |
|||||
|
x2 |
- 4 |
|
|||||||||
|
x ®2ê |
|
|
|
|
|||||||
|
ë |
|
|
|
|
|
|
|
|
|
||
593. |
lim |
tg x - sin x |
. |
||||
|
|
|
|
|
|||
|
x ®0 |
|
x3 |
||||
595. |
lim |
|
sin 4x |
||||
|
|
|
|
|
|
||
|
x ®0 |
|
x + 1 - 1 |
||||
|
|
|
|
|
|
|
|
597. |
lim |
2x sin x |
. |
||||
|
|||||||
|
x ®0 sec x - 1 |
||||||
599. lim 1 - cos 2x + tg2 x
|
|
|
x ®0 |
x sin x |
- |
1 |
ù |
|
|
|
( x -2)2 |
ú |
(положить x = 2 + a ). |
|
ú
û
601. 1) lim |
arcsin (x + 2) |
; |
2) lim |
cos (x + h) - cos (x - h) |
. |
||||
|
|
|
|||||||
x ®-2 |
x2 + 2x |
h ® 0 |
h |
||||||
602. lim |
|
|
sin2 x |
. |
|
|
|
||
|
|
|
|
|
|
|
|
||
x ®0 |
1 |
+ x sin x - cos x |
|
|
|
|
|||
|
|
|
|
|
|||||
|
§ 5. Неопределённости вида ¥ - ¥ и |
0 × ¥ . |
|
||||||
Рациональная функция – это частное от деления многочленов. Иррациональная – функция, содержащая иррациональное выражение
от независимой переменной.
123
При отыскании пределов от рациональных и иррациональных выражений необходимо овладеть умением раскрытия различных видов неопределенностей, в том числе вида ¥ - ¥ и 0 × ¥ . Естественно, дать общую схему раскрытия неопределенностей для всех случаев практически невозможно. Вместе с тем, для частных случаев можно использовать следующие приёмы:
1)если имеем неопределённость вида ¥ - ¥ и присутствует иррациональность, то предварительно, до перехода к пределу, необходимо избавиться от иррациональности в числителе или знаменателе(например, умножив и разделив на сопряженное), а затем находить предел.
2)неопределённость вида 0 × ¥ путем замены переменной или ряда
элементарных преобразований приводится к одному из видов |
0 |
|
|
или |
¥ |
|
, за- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
¥ |
|
|
|
|||||
дачи на раскрытие которых приведены в предыдущих параграфах. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
ö |
|||||||
603. |
|
|
x |
2 |
+ 3x - |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
lim |
ç |
|
|
|
|
÷ |
. |
|
|
|
|
|
|
|
|
604. |
limç |
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
÷ . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x ®+¥è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®1è x - 1 x2 - 1 ø |
||||||||||||||||||||||||
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
æ |
|
|
1 |
|
|
|
|
|
|
|
|
12 |
ö |
|||||||||
605. |
|
|
x |
2 |
+ x + 1 |
|
|
|
|
|
|
|
x |
2 |
- x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
lim |
ç |
|
|
|
|
- |
|
|
|
|
÷ . |
|
606. |
limç |
|
|
|
|
|
- |
|
|
|
|
|
|
|
÷ . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x ®+¥è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
x ®2è x - 2 x3 - |
8 ø |
|||||||||||||||||||||||
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ç |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
÷ |
|
|
|
|
|
é1 + 3 + ... + (2n - 1) |
|
|
ù |
||||||||||||||||||||||||||||||||
|
ç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
607. |
lim |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
608. |
limê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- nú . |
||||||||
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
x ÷ |
|
|
|
|
|
|
|
n + 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x ®0ç sin |
|
|
|
|
|
|
4 sin |
2 |
|
|
|
|
|
n ®¥ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|||||||||||||||||||||||||||
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
609. |
lim (1 - x)tg |
p |
x |
|
(положить x = 1 - a ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x ®1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ 1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
610. |
lim |
ç |
|
|
x |
|
+ 1 - |
|
x |
|
- 4x ÷ . |
611. |
lim ç |
|
|
+ |
|
|
|
|
|
|
|
|
÷ . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x ®-¥è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
x ®-2è x + |
2 x2 - |
ø |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
||||||||
612. |
lim |
|
|
|
|
|
|
x |
2 |
|
- x |
+ |
|
|
|
|
613. |
|
|
|
|
x |
2 |
- a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
ç x - |
|
|
|
|
|
1 ÷ . |
|
|
lim ç x - |
|
|
|
|
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x ®+¥è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
x ®+¥è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
614. |
|
æ sin x |
|
|
- tg |
2 |
x |
ö |
|
|
|
|
|
|
|
|
æ1 + 2 + 3 + ... + n |
|
|
n |
ö |
|
||||||||||||||||||||||||||||||||||
lim |
ç |
|
|
|
|
|
|
|
|
|
|
|
|
÷ . |
|
|
|
615. |
limç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
÷ . |
||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
n + 2 |
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||
|
x ®p / 2è cos 2 |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
n ®¥è |
|
|
|
|
|
|
|
|
|
|
ø |
|
||||||||||||||||||||||||
|
|
æ |
|
|
|
|
|
p |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
616. |
lim |
ç x |
- |
|
|
|
÷ tg x |
|
|
(положить x = |
|
+ a ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x ®p / 2 è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
§ 6. Непрерывность функции.
124
Функция y = f (x) называется непрерывной в точке x0 , если она определена в некоторой окрестности точки x0 и
lim f (x) = f (x0 ).
x ® x0
Последнее равенство означает, что:
1) функция f (x) должна быть определена в точке x0 и в ее окрестно-
сти;
2) должны существовать конечные пределы lim f (x) и |
lim f (x); |
x ® x0 - 0 |
x ® x0 + 0 |
3)эти пределы (слева и справа) должны быть одинаковыми;
4)эти пределы должны быть равны f (x0 ).
Функция называется непрерывной на отрезке [x1 , x2 ], если она непре-
рывна в каждой точке внутри отрезка, а на его границах lim f (x) = f (x1 ) и
x ® x1 + 0
lim f (x) = f (x2 ).
x ® x2 -0
Элементарные функции: степенная xn , показательная ax , логарифмическая, тригонометрические и им обратные, а также их сумма, произведение, частное непрерывны при всяком x , при котором они имеют определенное значение.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Различают два основных вида точек разрыва:
|
1) точки разрыва первого рода – когда существуют конечные пределы |
|||||||
lim |
f (x) и |
lim |
f (x), т.е. когда выполнено второе условие непрерывно- |
|||||
x ® x0 - 0 |
x ® x0 + 0 |
|
|
|
|
|
|
|
сти и не выполнены остальные (или хотя бы одно из них); |
|
|
||||||
|
2) точки разрыва второго рода– когда хотя бы один из пределов |
|||||||
lim |
f (x) или |
lim f (x) не существует или равен бесконечности. |
||||||
x ® x0 - 0 |
|
x ® x0 + 0 |
|
|
|
|
|
|
|
В свою очередь, точки разрыва первого рода делятся на: |
|||||||
|
а) точки устранимого разрыва – когда lim |
f (x) = |
lim f (x); |
|||||
|
|
|
x ® x0 -0 |
|
|
|
x ® x0 + 0 |
|
|
б) точки конечного разрыва – когда lim f (x) ¹ lim |
f (x). |
||||||
|
|
|
x ® x0 -0 |
|
x ® x0 +0 |
|||
|
|
|
Задания. |
|
|
|
|
|
|
617. Указать |
точку разрыва функцииy = |
|
4 |
|
, |
найти lim y , |
|
|
|
x - 2 |
||||||
|
|
|
|
|
|
x ®2-0 |
||
lim |
y , lim y |
и построить кривую по точкам x = – 2, 0, 1, 3, 4 и 6. |
||||||
x ®2 +0 |
x ®±¥ |
|
|
|
|
|
|
|
125

618. |
|
Найти точки разрыва и построить графики функций: |
|
|||||
1) y = - |
6 |
; |
2) y = tg x ; |
|
3) y = |
4 |
. |
|
|
|
4 - x2 |
||||||
|
x |
|
|
|
|
|
||
619. |
Построить график функции |
|
|
|
|
|||
|
|
|
|
ìx / 2 при |
x ¹ 2 |
|
||
|
|
|
|
y = í |
при x = 2 |
|
||
|
|
|
|
î0 |
|
|||
и указать точку ее разрыва. Какие из условий непрерывности в этой точке выполнены и какие не выполнены?
620. Построить графики функций: 1) y = |
x + 1 |
|
, 2) y = x + |
x + 1 |
. |
| x + 1 |
| |
|
|||
|
|
| x + 1 | |
|||
Какие из условий непрерывности в точках разрыва этих функций выполнены и какие не выполнены?
621. Построить график функции
ìsin x
ï при x ¹ 0, y = í x
ï2 при x = 0
î
и указать точку ее разрыва. Какие из условий непрерывности в ней выполнены и какие нет?
622. Указать точку разрыва функции y = 21 / x , найти lim y , |
lim y , |
x ®-0 |
x ®+0 |
lim y и построить график функции. Какие условия непрерывности в точке
x ®±¥
разрыва не выполнены?
623. Построить график функции
|
ì0,5x2 |
при | |
x |< 2 |
|
y = |
ï |
при |
| |
x |= 2 |
f (x) = í2,5 |
||||
|
ï |
при |
| |
x |> 2 |
|
î3 |
|||
иуказать точки ее разрыва.
624.Найти точки разрыва и построить графики функций
1) y = |
1 |
; |
2) y = arctg |
a |
; |
3) y = |
x3 - x2 |
||
|
|
|
|
. |
|||||
|
1 / x |
x - a |
|
||||||
|
1 + 2 |
|
|
|
|
2 | x - 1 | |
|||
625. Сколько однозначных функций задано уравнением x2 - y2 = 0 ?
Определить из них: 1) четную функцию; 2) нечетную функцию так, чтобы они имели конечные разрывы (I рода) при x = ±1, ± 2, ± 3,..., и построить их
графики.
|
626. Указать точку разрыва функцииy = |
x |
, найти |
lim y , |
|
x + 2 |
|||
|
|
|
x ®-2 -0 |
|
lim |
y , lim y и построить график по точкам x = -6, -4, -3, -1, 0, 2. |
|
||
x ®-2 +0 |
x ®±¥ |
|
|
|
126
627. Построить график функции
|
ì2 |
при x = 0 и x = ±2, |
y = |
ï |
- x2 при 0 <| x |< 2, |
f (x) = í4 |
||
|
ï |
при | x |> 2 |
|
î4 |
и указать точки разрыва. Какие условия непрерывности выполнены в точках разрыва и какие нет?
628. Найти точки разрыва и построить графики функций:
|
|
|
|
| x | |
|
|
|
1 |
|
1 |
|
|||||
1) |
y = 2 - |
; |
2) |
y = 2 |
x -2 |
; |
|
3) y = 1 - 2 |
x |
; |
||||||
|
||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
4) |
y = |
x3 |
+ x |
; |
5) |
y = |
|
4 - x2 |
|
. |
|
|
||||
2 | x | |
| 4x - x3 |
| |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
629. Сколько однозначных функций задано уравнением x2 + y 2 = 4 ? Определить из них: 1) две непрерывные на отрезке | x |£ 2 ; 2) ту из них, ко-
торая отрицательна на отрезке| x |£ 1 и положительна для всех остальных допустимых значений x . Построить график и указать разрывы последней функции.
Найти точки разрыва следующих функций и определить их тип:
630.y = x + 2 .
x- 4
632. |
y = log3 (1 - x). |
|||||
634. |
y = |
1 |
|
. |
|
|
|
x2 - 1 |
|
||||
636. |
y = |
|
2x |
. |
|
|
|
|
|
||||
|
|
|
sin x |
|
||
638. |
y = |
ìx + 1, |
x £ 0, |
|||
í |
|
|
x > 0. |
|||
|
|
î- x - 1, |
||||
|
æ |
p ö |
||
631. |
y = tgç x - |
|
÷ . |
|
4 |
||||
|
è |
ø |
||
633.y = x2 - 6x + 5 .
x2 - 7x + 6
-1
635.y = 3 x .
637. y = 2tg x .
639.y = x3 - 1 .
x- 1
§ 7. Второй замечательный предел.
Предел
æ |
|
1 |
ön |
|
|
1 |
|
limç1 |
+ |
|
÷ |
= lim(1 |
+ a ) |
|
= e |
n ®¥è |
|
n ø |
a ®0 |
|
a |
||
|
|
|
|
||||
называется вторым замечательным пределом.
Это число иррациональное и приближенно равно e » 2.71828 . Логарифмы с основанием e называются натуральными и обозначаются
127
loge x = ln x . Связь между десятичным и натуральным логарифмом определяется равенством: lg x = M ln x , где M » 0.43429 .
Пример 1. Известно, что формула сложных процентов имеет вид:
|
|
æ |
|
|
p |
ön |
|
||
Q |
= Q |
ç1 |
+ |
|
|
÷ |
, |
(1) |
|
100 |
|||||||||
|
0 |
è |
|
ø |
|
|
|||
где Q0 – первоначальная сумма вклада в банк, p – процент начисления за период времени (месяц, год), n – количество периодов времени хранения вклада в течение года, Q – сумма вклада по истечении n периодов хранения. Требу-
ется определить сумму депозита через x лет. |
|
|
|
|
|||||||||||||||
|
Решение: В общем случае, если p – процент начисления и год разбит |
||||||||||||||||||
на n |
частей, то формула (1) меняет вид, |
и через |
x лет сумма депозита |
||||||||||||||||
достигнет величины |
|
|
|
|
|
|
|
|
r ön x |
|
|
|
|
||||||
|
|
Q(n )= Q |
æ |
|
|
|
|
|
|
|
|||||||||
|
|
ç1 + |
|
|
|
÷ |
, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0 |
è |
|
|
n ø |
|
|
|
|
|
|
|||||
где r |
= p / 100 . Это выражение можно переписать так: |
|
|
||||||||||||||||
|
|
|
|
é |
|
|
|
|
r |
|
n |
|
ùr x |
|
|
|
|||
|
Q(n )= Q |
× ê |
æ |
|
|
|
ör |
ú . |
|
|
|
||||||||
|
ç1 |
+ |
|
|
|
|
÷ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
ê |
è |
|
|
|
n ø |
ú |
|
|
|
||||||
|
|
|
|
ê |
|
|
|
ú |
|
|
|
||||||||
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
Вводя новую переменную a = |
n |
и принимая во внимание, что a ® ¥ |
||||||||||||||||
|
r |
||||||||||||||||||
при n ® ¥ получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim Q(n )= |
lim Q × |
é æ |
|
|
1 öa |
ùr x |
Q × e |
r x |
. |
|||||||||
|
ê ç1 + |
|
|
|
|
÷ |
|
ú |
= |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
n ®¥ |
a ®¥ |
0 |
ê è |
|
|
a |
ø ú |
|
0 |
|
|
|||||||
|
|
|
|
ë |
|
|
|
|
|
|
|
|
û |
|
|
|
|
||
Расчеты, выполненные по этой формуле, называют вычислениями по непрерывным процентам.
Следует также отметить, что формулы вида(1) используются в демографических расчетах (прирост народонаселения) и в прогнозах макроэкономики (увеличение валового национального продукта).
Задания.
Найти пределы:
640. |
|
æ |
|
5 |
ön |
5 |
|
||
lim |
ç1 |
- |
|
÷ |
( положить - |
|
= a ). |
||
n |
n |
||||||||
|
n ®¥è |
|
ø |
|
|
||||
128
|
|
|
æ |
|
|
|
|
1 ön |
|
|
|
|
|
æ |
|
|
4 |
ön +3 |
||||||||||||||||||||
641. |
1) |
limç1 |
- |
|
|
|
|
|
÷ |
|
; |
|
|
|
2) |
lim |
ç1 |
+ |
|
|
|
÷ . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|||||||||||||||||||||||||||||
|
|
n ®¥è |
|
|
|
3n ø |
|
|
|
|
|
|
|
n ®-¥è |
|
|
|
ø |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- x |
|
|
|
|
||||||||||
642. |
1) |
lim(1 + 2x) |
|
|
|
; |
|
|
|
|
2) lim(1 - 4x) |
|
|
|
|
. |
|
|
|
|||||||||||||||||||
x |
|
|
|
|
|
x |
||||||||||||||||||||||||||||||||
|
|
x ®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
643. |
1) |
|
æ n |
|
|
|
ön |
; |
|
|
|
2) |
æ 2x |
- 1 ö |
2 x |
|||||||||||||||||||||||
limç |
|
|
|
|
÷ |
|
|
|
|
|
limç |
|
|
|
|
|
|
|
÷ . |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
n ®¥è n + 1 ø |
|
|
|
|
|
|
|
x ®¥è 2x |
+ 1 ø |
|
|
|
|
|
||||||||||||||||||||||
644. |
1) |
lim n [ln(n + 3) - ln n] ; |
|
|
2) lim (1 + 3 tg2 x)ctg2x . |
|||||||||||||||||||||||||||||||||
|
|
n ®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
645. |
lim (cos x)ctg2x |
|
|
(положить sin 2 x = a ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x ®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
646. |
1) |
lim |
ln(1 + a) |
; |
2) lim |
e-x - 1 |
; |
|
3) |
|
lim |
|
a2 x - 1 |
|||||||||||||||||||||||||
|
|
a |
|
x |
|
|
|
|
|
x |
|
|||||||||||||||||||||||||||
|
|
a ®0 |
|
|
|
|
|
x ®0 |
|
|
|
|
|
|
|
x ®0 |
|
|
||||||||||||||||||||
Указание. В примере 2) положить e-x - 1 = a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
647. |
Найти последовательные целые числа, между которыми содер- |
|||||||||||||||||||||||||||||||||||||
жится число 6 × (1 - 1.01-100 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Найти пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
648. |
1) |
|
æ |
|
|
|
|
2 ö3n |
|
|
|
|
|
|
æ n - 3 ön / 2 |
|||||||||||||||||||||||
limç1 |
+ |
|
|
÷ |
|
|
|
; |
|
|
|
2) |
limç |
|
|
|
|
÷ . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||||||||||||||||||||||
|
|
n ®¥è |
|
|
|
n ø |
|
|
|
|
|
|
|
n ®¥è |
|
ø |
|
|
|
|
|
|
|
|||||||||||||||
649. |
1) |
|
æ 3x |
- 2 ö |
2 x |
; |
|
|
2) |
lim |
e-3 x |
|
- 1 |
. |
|
|
|
|
||||||||||||||||||||
limç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x ®¥è 3x |
+ 1 ø |
|
|
|
|
|
|
x ®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
650. |
lim (sin x)ctg2x |
|
|
(положить cos 2 2x = a ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x ®p / 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
651. |
1) |
lim |
|
|
|
t |
|
|
; |
|
|
|
2) |
lim n [ln n - ln(n + 2)] . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
t ®0 ln(1 |
+ xt) |
|
|
|
|
n ® ¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Тестовые задания к пятой главе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Задание { 1 }. Если, в случае числовой последовательности {xn }, |
существует |
|||||||||||||||||||||||||||||||||||||
такое число M > 0 , что для " n Î N выполняется неравенство |
|
|
xn |
|
£ M , то |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
такую последовательность называют |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
- : ограниченной, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- : возрастающей, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
- : убывающей, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- : монотонной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
129
