- •Тема 1. Определители.
- •1.Перестановки.
- •2,3.Свойства.
- •4. Теорема (о знаке члена определителя.)
- •5. Понятие определителя произвольного порядка.
- •6.Свойства определителей.
- •Тема 2. Матрицы, ранг матрицы.
- •1.Матрицы
- •2.Ранг матрицы
- •3. Теорема о базисном миноре, теорема о ранге матрицы, теорема об элементарных преобразованиях матрицы.
- •4. Нахождение ранга матрицы с помощью элементарных преобразований.
- •5.Обратная матрица её свойства.
- •Тема 3. Системы линейных алгебраических уравнений.
- •1.Системы линейных алгебраических уравнений.
- •2. Основные определения: общее решение, частное решение, совместные и несовместные системы, эквивалентность систем.
- •3. Квадратные системы линейных алгебраических уравнений.
- •4. Теорема Крамера. Критерий совместности систем линейных уравнений общего вида (теорема Кронекера-Капелли).
- •5.Метод Гаусса решения систем линейных алгебраических уравнений.
- •6.Базисные и свободные неизвестные.
- •7. Однородные системы. Свойства решений (существование, линейность множества решений).
- •8.Фундаментальная система решений.
- •9.Теорема о числе векторов в фундаментальной системе решений.
- •Тема 4. Линейные пространства.
- •2. Аксиоматика линейного пространства, свойства, вытекающие из определения.
- •3.Примеры линейных пространств.
- •4.Линейно зависимые и линейно независимые системы векторов и их свойства.
- •5.Базис и размерность линейного пространства.
- •6. Конечномерные и бесконечномерные пространства.
- •7.Координаты вектора в данном базисе.
- •8. Матрица перехода от одного базиса к другому, преобразование координат вектора при переходе к новому базису.
- •9.Подпространство.
- •10. Линейные оболочки, теорема об их размерности.
- •Тема 5. Линейные операторы.
Тема 1. Определители.
1.Перестановки.
Опр.
Упорядоченная совокупность чисел
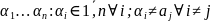 наз. перестановкой.
наз. перестановкой.
1, 2, …n – натуральная перестановка
Преобразование перестановки, при которой2а элемента меняются местами, наз. транспозицией.
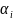 и
и
 образ. инверсию, если
>
при i<j,
и создает порядок при
<
при i<j.
Если число инв. четное, то перестановка
называется четной.
Общее число инв.
образ. инверсию, если
>
при i<j,
и создает порядок при
<
при i<j.
Если число инв. четное, то перестановка
называется четной.
Общее число инв.
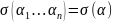
2,3.Свойства.
Свойства Перестановок.
1) Общее число перестановок из n элемента есть n!
 – n-способов
поставить элемент на 1е место.
– n-способов
поставить элемент на 1е место.
n(n-1) – max из 2ух элементов => длина элемента n(n-1)(n-2)…1=n!
2) Каждая транспозиция меняет четность перестановок.

1. Транспозиция соседних элементов

а) не влияет на число инв. отношение других элементов.
б) если < получим инв. при перест., > получим порядок при перестановке.
2.

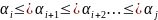
С помощью k+1 транспозиции
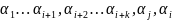
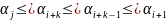
С помощью k транспозиции
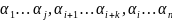 =>
2k+1-
общее число транспозиций => четность
перестановок меняется.
=>
2k+1-
общее число транспозиций => четность
перестановок меняется.
3. Все n! перестановки из n чисел могут быть упорядочены так, что каждая последняя отличается от предыдущей на 1, это упорядочение можно начать с любой перестановки
n=2; n!=2 (1;2) (2;1) (2;1) (1;2)
Пусть верно при (n-1). Док. при n:
 перест.
из n
эл.
перест.
из n
эл.
из n-1(n-1)! перестановка из (n-1) элемента = > по предположению индукции.
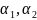 – меняем
местами
– меняем
местами

Следствие 1.
n>2 => число четных перестановок = числу нечет.
Упорядочение: четные перестановки -> нечетных перестановок и т.д. n! (n>2) – чет.
Следствие 2.
От
 перест. из n
чисел можно перейти к другой за конечное
число транспозиции.
перест. из n
чисел можно перейти к другой за конечное
число транспозиции.
4)
Если
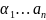 – перест. с числом инв. =S,
то после преобразования ее в натуральную
перестановку ее индексные номера
образуют перестановку с тем же числом
инв.
– перест. с числом инв. =S,
то после преобразования ее в натуральную
перестановку ее индексные номера
образуют перестановку с тем же числом
инв.
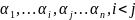
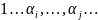 и
и
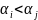 (нет инв.)
(нет инв.)
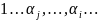 и
и
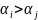 (инв.)
(инв.)
4. Теорема (о знаке члена определителя.)
Знак
члена определителя
 совпадает со знаком
совпадает со знаком
 ,
где S –число инверсий в
перестановке
,
где S –число инверсий в
перестановке
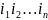 t-число
инверсий в перестановке
t-число
инверсий в перестановке
 индексов
столбцов.
индексов
столбцов.
[ ]
Допустим,
что четность числа S+t
не меняется если в члене определителя
(5) поменять местами два любых элемента.
Пусть это будут для определенности

 (6)
(6)
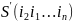 -число инверсий в перестановке
-число инверсий в перестановке
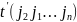 - число инверсий в перестановке
- число инверсий в перестановке
По
теореме
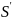 изменилась
на 1,
изменилась
на 1,
 - изменилась на 1
- изменилась на 1
Поэтому
числа
 ,
,
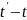 являются нечетными.
являются нечетными.
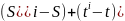 -
число четное,
-
число четное,
 -
число четное
-
число четное
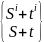 -одинаковой четности числа
-одинаковой четности числа
В произведении (6) расположим в порядке расположения следования строк
(7)
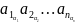

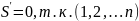
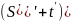 и S+t
и S+t


[///]
5. Понятие определителя произвольного порядка.
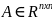
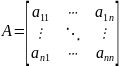
 – образ.
перест.
– образ.
перест.
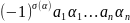
Опр.
Опред. квад. м. n-го
порядка наз. ∑ всевозм. произв. эл. м.,
взятых по 1му из каждой строки и каждого
столбца, причем если эти сомнож. упоряд.
по возраст. строк, то это произв. берется
со знаком
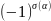 .
.
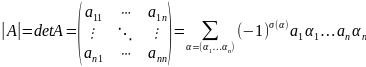
 – член
опред.
– член
опред.
– знак члена опред.
n>2=> число полож. членов – числу отриц.
6.Свойства определителей.
1) Опред. треуг. м. равен произвед. диаг. эл.
2)
Равноправ. строк и столбцов.
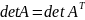
 – перест.
индексных
номеров
– перест.
индексных
номеров
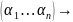 (1…n)=>
sgn
члена опред. не меняется.
(1…n)=>
sgn
члена опред. не меняется.
3) Если в м. есть нулевая строка(столбец), то detA=0
4) При умнож. строки(столбца) м. на число detA умнож. на это же число.
5) Если в опред. какая-либо строка(столбец) представ. в виде ∑ 2х других, то detA равен ∑ опред.

6) При перест. 2х строк(стол) м. опред. меняет sgn.
7) detA, имеющий 2е= строки = 0
8) Если 1а строка есть лин. комбин. других, то detA=0
9) Если к какой-либое строке +лин. комб. других строк, то detA не меняется.
Опр.