
- •Тема 1. Определители.
- •1.Перестановки.
- •2,3.Свойства.
- •4. Теорема (о знаке члена определителя.)
- •5. Понятие определителя произвольного порядка.
- •6.Свойства определителей.
- •Тема 2. Матрицы, ранг матрицы.
- •1.Матрицы
- •2.Ранг матрицы
- •3. Теорема о базисном миноре, теорема о ранге матрицы, теорема об элементарных преобразованиях матрицы.
- •4. Нахождение ранга матрицы с помощью элементарных преобразований.
- •5.Обратная матрица её свойства.
- •Тема 3. Системы линейных алгебраических уравнений.
- •1.Системы линейных алгебраических уравнений.
- •2. Основные определения: общее решение, частное решение, совместные и несовместные системы, эквивалентность систем.
- •3. Квадратные системы линейных алгебраических уравнений.
- •4. Теорема Крамера. Критерий совместности систем линейных уравнений общего вида (теорема Кронекера-Капелли).
- •5.Метод Гаусса решения систем линейных алгебраических уравнений.
- •6.Базисные и свободные неизвестные.
- •7. Однородные системы. Свойства решений (существование, линейность множества решений).
- •8.Фундаментальная система решений.
- •9.Теорема о числе векторов в фундаментальной системе решений.
- •Тема 4. Линейные пространства.
- •2. Аксиоматика линейного пространства, свойства, вытекающие из определения.
- •3.Примеры линейных пространств.
- •4.Линейно зависимые и линейно независимые системы векторов и их свойства.
- •5.Базис и размерность линейного пространства.
- •6. Конечномерные и бесконечномерные пространства.
- •7.Координаты вектора в данном базисе.
- •8. Матрица перехода от одного базиса к другому, преобразование координат вектора при переходе к новому базису.
- •9.Подпространство.
- •10. Линейные оболочки, теорема об их размерности.
- •Тема 5. Линейные операторы.
5.Базис и размерность линейного пространства.
Опр. Базис - упорядоченная система ЛНЗ векторов, такая что через нее выражается любой вектор прост-ва.
Опр.
Размерностью ЛП назы-ся число
векторов базиса. Размерность нулевого
прост-ва = 0;
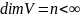 конечномерное прост-во.
конечномерное прост-во.
Опр.
ЛП назы-ся беск. мерным
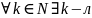 инейно
независ. векторов
инейно
независ. векторов
Если
ЛП св. векторов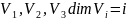
6. Конечномерные и бесконечномерные пространства.
Линейное пространство называется конечно-мерным , если для него существует конечная порождающая с.в., и бесконечномерным в противоположном случае

7.Координаты вектора в данном базисе.
Если система векторов e1, ..., en n-мерного линейного пространства Ln образует базис в Ln, то любой вектор x из Ln может быть представлен в виде
x = С1·e1+ С2·e2+ ...+ Сn· en.
Выражение x = С1·e1+ С2·e2+ ...+ Сn· en называется разложением вектора по базису e1, ..., en, а числа С1, С2, ..., Сn называются координатами вектора x в базисе e1, ..., en.
Координаты вектора принято обозначать тем же символом, что и сам вектор:
x = x1·e1+ x2·e2+ ...+ xn· en.
Взаимно однозначное соответствие x = x1·e1+ x2·e2+ ...+ xn· en ⇐⇒ x = (x1, x2, ..., xn)
— изоморфизм Ln и Rn
8. Матрица перехода от одного базиса к другому, преобразование координат вектора при переходе к новому базису.
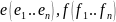 - базисы в V
- базисы в V
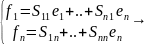
S= -
матрица перехода от e
к f.
-
матрица перехода от e
к f.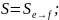
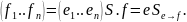
Теорема.
 -
невырожден.
-
невырожден.
Док-во:
Пусть
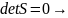
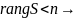 есть строка(столб.),
есть строка(столб.),
который явл. линейн. комб.
Других
строк(столб.) -ЛЗ.
-ЛЗ.
Теорема.
Если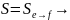
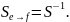
Док-во: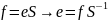 .
.
Теорема.
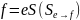 .
Тогда
.
Тогда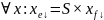 .
.
Док-во:
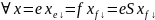
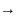 единств. разложение
единств. разложение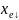 =
=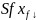
9.Подпространство.
Опр. L c V - подмно-во ЛП наз-ся ЛПЛП, если
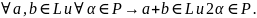
10. Линейные оболочки, теорема об их размерности.
Опр.
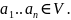 Линейн. оболочка
-
Линейн. оболочка
-
мн-во
всех линейн. комбинаций; L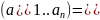
{x=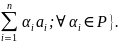
Теорема. Линейн. оболочка сама явл. ЛП.
Теорема. dimL max числу ЛНЗ
эл-тов .
Док-во: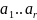 -
ЛНЗ,
-
ЛНЗ,
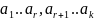 ;
;
dimL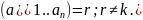 Вся
сист. ЛЗ;
Вся
сист. ЛЗ;
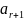 -
лин. комб.
-
лин. комб.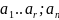 -лин.
комб.
-лин.
комб.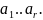
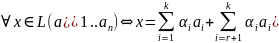
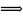 x
- лин. комб.
x
- лин. комб.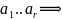 базис
базис
dimL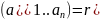
Тема 5. Линейные операторы.
1.Линейные операторы в конечномерном линейном пространстве.
2. Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.
Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.
Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.
Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:
A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u).
3. Примеры.
1)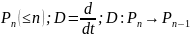 .
.
2)Нулев.
оператор: .
.
3)Y-тождественный оператор:
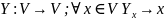 .4)
.4)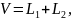
P-оператор
проектирования на
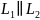
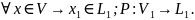
4.Матрица линейного оператора в данном базисе
V,W
над Р. dimV=n;
e=(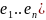 -базис
в V;
-базис
в V;
dimW=m;
f=( -
базис в W,
-
базис в W,
A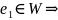 разл.по
базису.
разл.по
базису.
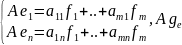 =
=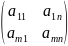
-матрица л.о. А в паре базисов f, e
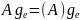 ;
A:V
;
A:V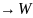 ;
;
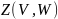 -
мн-во всех
-
мн-во всех
Л.о. из V в W.
5.Связь между линейными операторами и квадратными матрицами.
Связь
между матрицами линейного оператора в
разных базисах:
![]() M(φ)
- матрица Л.О. φ в старом базисе.
M1(φ)
- матрица Л.О. φ в новом базисе.
Т -
матрица перехода от старшего базиса к
новому базису.
M(φ)
- матрица Л.О. φ в старом базисе.
M1(φ)
- матрица Л.О. φ в новом базисе.
Т -
матрица перехода от старшего базиса к
новому базису.
6. .Преобразование матрицы оператора при переходе от одного базиса к другому.
Теорема:(мат-цы оператор. в разл. базис.)
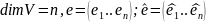
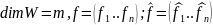
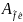 =
=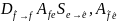 =
=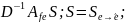
D=
Док-во:
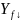 =
=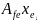 =
=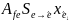 ,
,
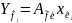
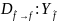 =
=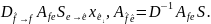
Следствия:
1)D,S
- невырожд. матрицы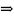
матрицы л.о. в разн. базисах эквивалент.
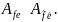 2)rang матр. л.о. не
изм. при
2)rang матр. л.о. не
изм. при
переходе к др. базису.
Теорема:
A,B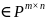 -
эквивалент.
-
эквивалент.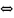 А
и В
А
и В
- матрицы одного л.о. в разных базисах.
Док-во:"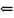 "Следствие
1)
"Следствие
1)
"
"A
 B
B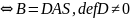 ;defS
;defS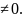
V-зафиксирован. базис в e; dimV=n;
W-зафиксирован. базис.
Пусть
А- матр. А:V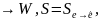 D=
D=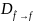
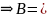 .
.
