
- •Тестовые задания к первой главе
- •Две матрицы называются равными, если равны их
- •Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется
- •Построение обратной допускает матрица
- •Построение обратной допускает матрица
- •Тестовые задания ко второй главе.
- •Взаимно перпендикулярными векторами являются
- •Тестовые задания к третьей главе.
- •Уравнение прямой с угловым коэффициентом имеет вид:
- •Уравнение прямой, проходящей через данную точку имеет вид:
- •Уравнение прямой, проходящей через две точки имеет вид:
- •Общее уравнение прямой имеет вид:
- •Уравнение прямой в отрезках имеет вид:
- •Нормальное уравнение прямой имеет вид:
- •Полярное уравнение прямой имеет вид:
- •Каноническое уравнение гиперболы, у которой расстояние между фокусами равно 10 и действительная ось равна 8, имеет вид:
- •Каноническое уравнение параболы, в случае, когда расстояние между фокусом и вершиной равно 3 имеет вид:
- •Общее уравнение плоскости имеет вид:
- •Уравнение плоскости в отрезках на осях имеет вид:
- •Нормальное уравнение плоскости имеет вид:
- •Точки, в которых нарушается непрерывность функции, называются
- •Если в точке разрыва функции существуют конечные пределы функции слева и справа, то эта точка называется точкой
- •Первым замечательным пределом является предел
- •Вторым замечательным пределом является предел

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КАБАРДИНО-БАЛКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СБОРНИК ЗАДАЧ ПО ВЫСШЕЙ МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ ЭКОНОМИЧЕСКОГО ФАКУЛЬТЕТА
ЧАСТЬ 1
НАЛЬЧИК 2004
УДК 519.6 ББК 22.11
Рецензент:
кандидат физико-математических наук, старший научный сотрудник НИИ ПМА КБНЦ РАН
А.В. Псху
Составители: Лесев В.Н., Кучмазокова Л.С.
Сборник задач по высшей математике для студентов экономического факультета. Часть 1. – Нальчик: Каб.-Балк. ун-т, 2004.
За основу издания был выбран популярный сборник задач В.П. Минорского [10], дополненный новыми заданиями и задачами по экономике. Имеется обширная подборка задач для самостоятельных упражнений и контрольных заданий.
Предназначено для студентов всех форм обучения экономических и смежных технических специальностей.
Рекомендовано РИСом университета
УДК 519.6 ББК 22.11
ÓКабардино-Балкарского государственного университет, 2004
2
ГЛАВА 1. ЛИНЕЙНАЯ АЛГЕБРА
§1. Матрицы. Действия над матрицами
Матрица – это прямоугольная таблица чисел, содержащая m строк и n столбцов:
æ a |
a |
K a |
ö |
|
ç |
11 |
12 |
1n |
÷ |
ç a21 |
a22 |
K a2 n ÷ |
||
ç |
L |
L |
L L |
÷ . |
ç |
÷ |
|||
ç |
|
am 2 |
|
÷ |
èam1 |
K amn ø |
|||
Эту матрицу обозначают A = (aij ), где 1 £ i £ m , 1 £ j £ n и говорят,
что ее размер m ´ n . Числа aij , из которых составлена матрица, где i -номер строки, j -номер столбца, называют элементами матрицы. Элементы мат-
рицы для которых i = j |
образуют главную диагональ матрицы. |
|
Чтобы матрицу |
произвольного |
размера A = (aij ) умножить на число |
l , нужно каждый элемент матрицы aij |
умножить на число l . |
|
Две матрицы одного размера A = (aij ) и B = (bij ) можно складывать.
При этом, результатом сложения будет новая матрица C = (cij ) того же размера, что и исходные матрицы, элементы которой определяются равенствами
cij = aij + bij .
Произведение матриц A ´ B определено при условии, что левая матрица A имеет столько столбцов, сколько строк у правой матрицы B . Поэтому, пусть матрица A имеет p строк и q столбцов, а матрица B – q строк и
r столбцов. Тогда |
результатом |
произведения A ´ B |
будет |
новая матрица |
C = (cij ), имеющая |
p строк, r |
столбцов, элементы |
которой |
определяются |
q
равенствами cij = å aik bkj .
k =1
Пример 1. На предприятии выпускается 4 вида изделий при использовании 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы
A :
æ2 |
3 |
4 |
5 |
ö |
|
|
ç |
|
2 |
5 |
6 |
÷ |
|
ç1 |
÷ |
, |
||||
A = ç |
7 |
2 |
3 |
2 |
÷ |
|
ç |
÷ |
|
||||
ç |
4 |
5 |
6 |
8 |
÷ |
|
è |
ø |
|
||||
где строки – вид изделия, а столбцы – вид сырья.
3
Необходимо найти затраты сырья на каждый вид изделия при заданном плане их выпуска: соответственно 60, 50, 35 и 40 ед.
Решение: Составим матрицу-строку, определяющую план выпуска продукции: q = (60 50 35 40). Тогда решение задачи находится как произведение матрицы q на матрицу А:
æ2 |
3 |
4 |
5ö |
æ |
120 + 50 + 245 + 160 |
ö |
æ |
575 |
ö |
||
ç |
|
2 |
5 |
|
÷ |
ç |
180 + 100 + 70 + 200 |
÷ |
ç |
|
÷ |
ç1 |
6÷ |
ç |
÷ |
ç550 |
÷ |
||||||
q × A = (60 50 35 40)× ç |
7 |
2 |
3 |
2 |
÷ |
= ç |
240 + 250 + 105 + 240 |
÷ |
= ç |
835 |
÷ . |
ç |
÷ |
ç |
÷ |
ç |
÷ |
||||||
ç |
4 |
5 |
6 |
8 |
÷ |
ç |
300 + 300 + 70 + 320 |
÷ |
ç |
990 |
÷ |
è |
ø |
è |
ø |
è |
ø |
||||||
Матрица, полученная из данной заменой всех ее строк столбцами с со-
хранением номера, называется транспонированной и обозначается AT .
Пример 2. Пусть затраты 4-х видов сырья на выпуск4-х видов продукции характеризуется матрицей A , приведенной в примере 1. Требуется найти общие затраты на сырье для каждого вида продукции и его перевозку, если известны себестоимости каждого вида сырья и его доставки(соответственно 4, 6, 5, 8 и 2, 1 ,3 , 2 ден. ед.).
Решение: Составим матрицу себестоимостей сырья и его доставки:
æ4 |
6 |
5 |
8 |
ö |
|
ç |
|
|
|
|
÷ |
С = ç |
2 |
1 |
3 |
2 |
÷ . |
è |
ø |
||||
Тогда ответ на вопрос задачи дается в виде произведения матрицы A на транспонированную матрицу C T :
|
|
|
|
|
|
|
æ |
2 3 4 5ö |
|
æ |
4 2ö |
æ 86 29 |
ö |
||||
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
ç |
|
÷ |
ç |
÷ |
|
|
|
A × CT |
|
|
ç1 2 5 6÷ |
|
ç6 1 ÷ |
ç 89 31÷ |
||||||||
|
|
|
|
= |
ç |
7 2 3 2 |
÷ |
× |
ç |
5 3 |
÷ |
= ç |
÷ . |
||||
|
|
|
|
|
|
|
ç |
÷ |
|
ç |
÷ |
ç 71 29 |
÷ |
||||
|
|
|
|
|
|
|
ç |
4 |
5 6 8 |
÷ |
|
ç |
8 2 |
÷ |
ç |
÷ |
|
|
|
|
|
|
|
|
è |
ø |
|
è |
ø |
è140 47 |
ø |
||||
|
|
|
|
|
|
|
|
|
|
Задания |
|
|
|
||||
|
Сложить матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
æ |
1 |
12 ö |
|
æ2 |
|
- 10ö |
|
|
|
|
|
|
|
|
||
1. |
ç |
|
÷ |
= |
ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
|
A = ç |
0 |
÷ , B |
ç |
2 |
|
|
÷ |
|
|
|
|
|
|
|
|||
|
è |
- 3ø |
|
è |
|
|
7 ø |
|
|
|
|
|
|
|
|
||
2. |
æ- 2 |
4 ö |
= |
æ |
3 |
|
- 4ö |
|
|
|
|
|
|
|
|||
A = ç |
|
÷ , B |
ç |
|
|
|
÷ , |
|
|
|
|
|
|
|
|||
|
ç |
7 |
÷ |
|
|
ç |
|
|
2 |
÷ |
|
|
|
|
|
|
|
|
è |
- 1ø |
|
|
è- 7 |
ø |
|
|
|
|
|
|
|
||||
|
æ |
1 4 2 ö |
|
|
|
æ 2 - 1 4 |
|
ö |
|
|
|
||||||
|
ç |
|
÷ |
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
3. A = ç- 1 3 0 ÷ , B = ç 0 |
4 - 1÷ , |
|
|
|
|||||||||||||
|
ç |
|
÷ |
|
|
|
ç |
- 4 |
- 2 3 |
|
÷ |
|
|
|
|||
|
è |
9 8 - 1ø |
|
|
|
è |
|
ø |
|
|
|
||||||
4
æ11 0 |
|
4 |
ö |
æ - 5 3 |
1 ö |
||||
ç |
|
|
|
|
÷ |
ç |
|
|
÷ |
4. A = ç 7 - 1 3 ÷ , B = ç- 2 6 |
3 ÷ , |
||||||||
ç |
1 6 |
- 6 |
÷ |
ç |
- 4 10 |
÷ |
|||
è |
ø |
è - 1 |
ø |
||||||
æ3 |
2 |
1 |
ö |
æ- 2 - 2 - 1 |
ö |
|
|||
ç |
|
1 |
|
÷ |
ç |
|
|
÷ |
|
5. A = ç2 |
3÷ , |
B = ç- 2 |
0 - 3÷ . |
|
|||||
ç |
0 |
- 1 |
2 |
÷ |
ç |
0 |
1 - 1 |
÷ |
|
è |
ø |
è |
ø |
|
|||||
Умножить матрицу A на число l :
|
æ0 |
1 ö |
, l = 3 , |
|
|
|
|
|
|
7. |
æ |
2 |
4 ö |
, l = -0.5 , |
|||||||
6. A = ç |
|
|
÷ |
|
|
|
|
|
|
A = ç |
|
|
÷ |
||||||||
|
ç |
2 |
- |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
- 6 |
- |
÷ |
|
|
è |
1ø |
|
|
|
|
|
|
|
|
|
|
|
|
è |
8ø |
|
||||
|
æ- 13 0 - 2ö |
|
|
|
|
|
|
|
|
æ4 1 0 ö |
|||||||||||
8. |
ç |
|
|
|
|
|
÷ |
l = -2 , |
|
|
ç |
|
|
|
÷ |
||||||
A = ç 4 |
0 - 5÷ , |
|
9. A = ç6 - 3 2÷ , l = -3 , |
||||||||||||||||||
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
ç |
0 |
- 4 0 |
÷ |
||
|
è |
- 6 7 12 ø |
|
|
|
|
|
|
|
|
è |
ø |
|||||||||
|
|
æ- 7 |
|
8 |
14ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ç |
|
|
|
|
÷ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
10. |
A = ç 12 |
|
5 |
|
6 ÷ , |
l = |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ç |
2 |
|
4 |
|
÷ |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
è |
|
10ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найти произведение матриц A ´ B , если |
|
|
|
|
||||||||||||||||
11. |
A = |
æ |
2 |
1 ö |
, |
|
|
æ1 - 5ö |
|
|
|
|
|
|
|
||||||
ç |
|
|
÷ |
B = ç |
|
|
|
÷ , |
|
|
|
|
|
|
|
||||||
|
|
ç |
|
- |
÷ |
|
|
|
ç |
0 |
÷ |
|
|
|
|
|
|
|
|||
|
|
è- 1 |
3ø |
|
|
|
è0 |
ø |
|
|
|
|
|
|
|
||||||
12. |
A = |
æ1 - 2ö |
|
B = |
æ9 |
- 1ö |
|
|
|
|
|
|
|
||||||||
ç |
|
|
÷ , |
ç |
|
|
|
|
÷ , |
|
|
|
|
|
|
|
|||||
|
|
ç |
|
|
÷ |
|
|
|
ç |
0 |
2 |
÷ |
|
|
|
|
|
|
|
||
|
|
è0 |
- 1 ø |
|
|
|
è |
ø |
|
|
|
|
|
|
|
||||||
|
|
æ 2 - 1 2 ö |
|
|
æ |
1 |
1 0 ö |
|
|
|
|
|
|||||||||
|
|
ç |
|
|
1 |
|
|
÷ |
|
|
ç |
|
1 |
÷ |
|
|
|
|
|
||
13. A = ç- 1 |
|
|
0 ÷ , |
B = ç- 1 |
- 1÷ , |
|
|
|
|
|
|||||||||||
|
|
ç |
0 |
|
2 - |
÷ |
|
|
ç |
|
|
÷ |
|
|
|
|
|
||||
|
|
è |
|
1ø |
|
|
è |
0 1 1 ø |
|
|
|
|
|
||||||||
|
|
æ4 2 1ö |
|
|
æ 10 |
|
0 - 1ö |
|
|
|
|
|
|||||||||
|
|
ç |
|
6 |
|
÷ |
|
|
ç |
|
|
|
6 |
|
÷ |
|
|
|
|
|
|
14. A = ç8 |
4÷ , |
B = ç- 3 |
|
3 ÷ , |
|
|
|
|
|
||||||||||||
|
|
ç |
3 6 9 |
÷ |
|
|
ç |
- 3 |
|
|
÷ |
|
|
|
|
|
|||||
|
|
è |
ø |
|
|
è |
- 4 0 ø |
|
|
|
|
|
|||||||||
|
|
æ7 - 2 10 ö |
|
|
æ1 2 - 1ö |
|
|
|
|
|
|||||||||||
15. |
|
ç |
|
- 3 |
|
|
÷ |
|
|
ç |
10 |
|
÷ |
|
|
|
|
|
|||
A = ç0 |
32÷ , |
B = ç9 |
|
8 ÷ . |
|
|
|
|
|
||||||||||||
|
|
ç |
0 |
|
|
|
|
÷ |
|
|
ç |
|
|
÷ |
|
|
|
|
|
||
|
|
è |
- 2 21ø |
|
|
è2 1 1 ø |
|
|
|
|
|
||||||||||
|
Транспонировать матрицы: |
|
|
|
æa |
c ö |
|
|
|||||||||||||
|
|
æ17 |
- 31ö |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16. |
A = |
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
17. |
A = |
ç |
÷ |
, |
|
ç |
29 |
- 15 |
÷ , |
|
|
|
|
|
|
|
|
ç |
÷ |
|
|||||||
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
èb |
d ø |
|
|
||||
5

|
æ25 - 1 |
9 ö |
æ1 - 4 7 - 10ö |
||||||
18. |
ç |
- 2 |
|
|
÷ |
ç |
- 5 8 |
÷ |
|
A = ç68 |
|
8 ÷ , |
19. A = ç2 |
- 11÷ , |
|||||
|
ç |
- 3 |
7 |
÷ |
ç |
- 6 9 |
÷ |
||
|
è91 |
ø |
è3 |
- 12ø |
|||||
|
æ11 |
0 |
5 |
ö |
|
|
|
|
|
|
ç |
3 |
8 |
÷ |
|
|
|
|
|
20. |
ç 6 |
÷ |
|
|
|
|
|||
A = ç |
|
|
|
÷ . |
|
|
|
|
|
|
ç 4 |
2 |
7 |
÷ |
|
|
|
|
|
|
ç |
0 |
9 |
÷ |
|
|
|
|
|
|
è13 |
ø |
|
|
|
|
|||
§2. Определители и их свойства. Ранг матрицы
Определителем квадратной матрицы A называется число, равное сумме всех произведений элементов этой матрицы, взятых по одному из каждой строчки и каждого столбца; при этом каждое произведение снабжено знаком плюс или минус по некоторому правилу. Определитель обозначается
A или det(A).
Определители матриц первого, второго и третьего порядков(размера 1 ´ 1, 2 ´ 2, 3´ 3) определяются равенствами
|
|
det(a |
) = |
|
a |
|
= a , |
æ a |
|
a |
ö |
= |
a |
a |
|
= a |
a |
|
- a a |
|
, |
|
|
|
|
detç |
11 |
12 |
÷ |
11 |
|
12 |
22 |
21 |
|||||||||
|
|
11 |
|
|
11 |
|
11 |
ç |
|
|
÷ |
|
|
|
|
11 |
|
12 |
|
||
|
a11 |
a12 |
a13 |
|
|
|
|
èa21 |
a22 |
ø |
|
a21 |
a22 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
- a13 a22 a31 -a12 a21a33 -a23 a32 a11 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a21 |
a22 |
a23 |
|
= a11a22 a33 +a12 a23 a31 +a21 a32 a13 |
||||||||||||||||
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель матрицы, полученной из исходной путем вычеркивания i -ой строки и j -го столбца, называется минором элемента aij и обозначается M ij .
Алгебраическим дополнением элемента aij называется выражение
Aij = (- 1)i + j M ij .
Минором k -го порядка матрицы A , содержащей m строк и n столбцов называется определитель матрицы, полученной из матрицы A путем вычеркивания произвольно выбранных m - k строк и n - k столбцов.
Минор матрицы A максимального порядка и отличный от нуля называется базисным. Порядок базисного минора называется рангом матрицы и обозначается r , r(A) или rang(A).
6
Приведем теперь некоторые свойства определителей:
1.Определители квадратных матриц A и AT равны.
2.Перестановка двух строк (столбцов) определителя меняет его знак. 3.Общий множитель элементов какой-либо строки(столбца) можно
выносить за знак определителя.
4.Если определитель содержит пропорциональные строки(столбцы), то он равен нулю.
5.Определитель не измениться, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки(столбца), умноженные на произвольное число.
6.Определитель разлагается по элементам строки(столбца), т.е. равен сумме произведений элементов некоторой строки(столбца) на соответст-
вующие им алгебраические дополнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Вычислить определители: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
21. |
|
3 |
- 2 |
|
, |
|
|
|
|
22. |
|
2 |
3 |
|
, |
|
|
|
23. |
|
3 |
- 2 |
|
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
4 |
6 |
|
|
|
|
|
|
|
|
6 |
- 10 |
|
|
|
|
|
|
|
- 4 |
5 |
|
|
|
|
|
|
|
||
|
|
|
|
|
- |
1 |
|
, |
|
|
sin a |
|
cos a |
|
|
|
sin 2 a |
cos 2 a |
|
, |
|||||||||||
24. |
|
|
a |
|
|
25. |
|
|
, |
26. |
|
|
|||||||||||||||||||
|
|
a |
|
|
a |
|
|
|
- cos a |
|
sin a |
|
|
|
sin2 |
b |
cos2 b |
|
|
||||||||||||
27. |
|
1 |
0 |
2 |
|
, |
28. |
|
3 |
- 1 |
0 |
|
, |
|
29. |
|
2 |
5 |
7 |
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
0 |
2 |
3 |
|
|
1 |
- 1 |
- 2 |
|
|
|
- 2 |
2 |
0 |
|
|
|
||||||||||||||
|
|
3 |
4 |
0 |
|
|
|
|
|
|
1 |
- 1 2 |
|
|
|
|
|
- 6 0 1 |
|
|
|
|
|||||||||
Вычислить определители, разложив по элементам первого столбца:
|
2 |
3 |
4 |
|
|
a |
1 |
a |
|
30. |
5 |
- 2 |
1 |
, |
31. |
- 1 |
a |
1 |
. |
|
1 |
2 |
3 |
|
|
a |
- 1 |
a |
|
Вычислить определители, разложив по элементам ряда, содержащего наибольшее число нулей:
|
1 |
b |
1 |
|
|
- x |
1 |
x |
|
32. |
0 |
b |
0 |
, |
33. |
0 |
- x |
- 1 |
. |
|
b |
0 |
- b |
|
|
x |
1 |
- x |
|
7
Упростить и вычислить определители:
|
|
2 - 3 1 |
|
|
|
|
12 |
6 - 4 |
|
|
|
1 |
|
2 |
5 |
|
|
|||||||
34. |
|
6 |
- 6 |
2 |
, |
|
35. |
|
6 |
4 |
4 |
|
, |
36. |
|
3 |
|
- 4 |
7 |
, |
|
|||
|
|
2 - 1 2 |
|
|
|
|
3 2 8 |
|
|
|
|
- 3 12 - 15 |
|
|
||||||||||
|
|
a - a a |
|
|
|
x2 |
x 1 |
|
|
|
|
|
|
m + a m - a |
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
37. |
|
a |
a |
- a |
, |
38. |
|
y2 |
y |
1 |
|
, |
|
|
39. |
|
n + a 2n - a |
a |
. |
|||||
|
|
a - a - a |
|
|
|
z 2 |
z 1 |
|
|
|
|
|
|
|
a |
|
- a |
a |
|
|||||
|
|
|
Найти x |
из уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x2 |
4 |
9 |
|
|
|
|
|
x2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
40. |
|
x |
2 |
3 |
= 0 , |
41. |
|
x |
- 1 |
1 |
|
= 0 . |
|
|
|
|
|
|
|
|
||||
|
|
1 |
1 |
1 |
|
|
|
|
|
0 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Определить ранг матриц: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
æ1 1 1ö |
|
|
|
æ1 0ö |
|
|
|
|
|
|
æ1 1 1ö |
|
|
|
|||||||||
42. |
ç |
2 |
÷ |
|
|
43. |
ç |
÷ |
|
|
|
|
|
|
ç |
2 |
÷ |
|
|
|
||||
ç2 |
2÷ , |
|
ç0 |
0÷ , |
|
|
|
|
|
44. ç1 |
3÷ , |
|
|
|||||||||||
|
ç |
|
÷ |
|
|
|
ç |
÷ |
|
|
|
|
|
|
ç |
|
÷ |
|
|
|
||||
|
è3 3 3ø |
|
|
|
è0 0ø |
|
|
|
|
|
|
è1 4 9ø |
|
|
|
|||||||||
|
æ1 2 3 4ö |
|
æ0 2 1 0ö |
|
æ0 1 0 1ö |
|
|
|||||||||||||||||
45. |
ç |
5 |
6 |
|
|
÷ |
46. |
ç |
3 |
0 |
|
|
|
÷ |
|
ç |
1 |
3 |
÷ |
|
|
|||
ç0 |
|
7 ÷ , |
ç1 |
|
|
|
2÷ , |
47. ç2 |
1÷ . |
|
|
|||||||||||||
|
ç |
|
|
|
|
÷ |
|
ç |
|
|
|
|
|
÷ |
|
ç |
|
|
÷ |
|
|
|||
|
è0 0 0 0 |
ø |
|
è0 1 0 4ø |
|
è4 3 5 4ø |
|
|
||||||||||||||||
§3. Обратная матрица
Пусть A – квадратная матрица n -го порядка. Квадратная матрица того же порядка n называется обратной для матрицы A , если она при умножении на A слева и справа дает единичную матрицу. Обратная матрица обозначается через A-1 . Таким образом, для матриц A и A-1 выполняются равенства A ´ A-1 = A-1 ´ A = E .
Матрица
|
æ |
A |
A |
K A |
ö |
|
|
ç |
11 |
21 |
n1 |
÷ |
|
~ |
ç A12 |
A22 |
K An2 ÷ |
, |
||
A = ç |
L |
L |
L L |
÷ |
||
|
ç |
÷ |
|
|||
|
ç A |
A |
K A |
÷ |
|
|
|
è |
1n |
2n |
nn |
ø |
|
8
в строчках которой расположены алгебраические дополнения элементов соответствующих столбцов матрицы A , называется взаимной для A .
Для построения обратной матрицы необходимо:
1.Проверить, является ли заданная матрица невырожденной, т.е. возможно ли построение обратной матрицы(для этого определитель исходной матрицы A должен быть отличным от нуля).
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2.Составить взаимную матрицу A . |
|
|
|
|
|
|
|
1 |
~ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|||
|
|
|
|
3.Найти обратную матрицу по формуле A |
|
|
= |
|
A . |
|||||||||||||
|
|
A |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Проверить полученный результат по определению, т.е. проверить |
||||||||||||||||||
справедливость равенств A ´ A-1 |
= A-1 ´ A = E . |
|
|
|
|
|||||||||||||||||
|
|
|
|
Другими словами, если матрица |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
æ x |
x |
|
K x |
|
ö |
|
|
||||||||||
|
|
|
|
|
ç |
|
11 |
12 |
|
K x |
1n |
÷ |
|
|
||||||||
|
|
|
|
A-1 |
ç x |
21 |
x |
22 |
|
2n |
÷ |
|
|
|||||||||
|
|
|
|
= ç |
|
|
|
|
|
|
|
÷ |
|
|
||||||||
|
|
|
|
|
ç L |
L L L |
÷ |
|
|
|||||||||||||
|
|
|
|
|
ç |
|
|
|
|
xn 2 |
|
|
|
|
|
|
÷ |
|
|
|||
|
|
|
|
|
è xn1 |
|
K xnn ø |
|
|
|||||||||||||
является обратной для матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
æ a |
|
|
|
a |
|
K |
a |
|
ö |
|
|
|
|||||
|
|
|
|
|
ç |
|
11 |
|
|
12 |
|
|
|
1n |
÷ |
|
|
|
||||
|
|
|
|
|
ça21 |
a22 |
K a2n ÷ |
, |
|
|
||||||||||||
|
|
|
|
A = ç |
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|||
|
|
|
|
|
ç L |
L L L |
÷ |
|
|
|
||||||||||||
|
|
|
|
|
ç |
|
|
|
|
|
an2 |
|
|
|
|
|
÷ |
|
|
|
||
|
|
|
|
|
èan1 |
K ann ø |
|
|
|
|||||||||||||
то элементы x матрицы A-1 |
подсчитываются по правилу |
|||||||||||||||||||||
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
A |
ji |
= |
(- 1)j +i M |
ji |
, |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
ij |
|
|
A |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
A |
|
– определитель матрицы A , Aji |
– алгебраические дополнения эле- |
|||||||||||||||||
|
|
|||||||||||||||||||||
ментов a ji , а M ji – миноры элементов a ji . |
|
|
|
|
|
|
|
|||||||||||||||
Задания
Найти обратные матрицы для следующих матриц:
|
æ |
1 - 2ö |
|
|
æ 7 |
- 4 |
ö |
|
|
|
æ13 5 ö |
|
|||||
48. |
ç |
|
÷ |
, |
49. |
ç |
|
|
÷ |
, |
|
50. |
ç |
|
|
÷ |
, |
ç |
|
÷ |
ç |
- 5 |
3 |
÷ |
|
ç |
31 12 |
÷ |
|||||||
|
è |
- 5 11ø |
|
|
è |
ø |
|
|
|
è |
ø |
|
|||||
|
æ |
- 8 |
13 ö |
|
|
æ |
cos a |
sin a ö |
|
|
æa |
b ö |
|
|
|||
51. |
ç |
|
÷ |
, |
52. |
ç |
|
|
|
÷ |
, |
53. |
ç |
|
÷ |
, |
|
ç |
- 13 |
÷ |
ç |
- sin a |
|
÷ |
ç |
|
÷ |
|
|||||||
|
è |
21ø |
|
|
è |
cos a ø |
|
|
è c |
d ø |
|
|
|||||
9
|
æ2 |
|
5 |
7 ö |
|
æ 3 - 4 |
|
|
5ö |
|
|
|
|
|
|
æ |
2 7 3ö |
||||||
|
ç |
|
|
3 |
|
÷ |
|
ç |
- 3 |
|
|
÷ |
|
|
|
|
|
|
ç |
|
9 |
÷ |
|
54. ç6 |
|
4÷ , |
55. ç2 |
|
|
1÷ , |
|
|
|
|
56. ç3 |
4÷ , |
|||||||||||
|
ç |
5 |
- 2 - |
|
÷ |
|
ç |
- 5 |
|
|
÷ |
|
|
|
|
|
|
ç |
|
|
÷ |
||
|
è |
3ø |
|
è 3 |
|
- 1ø |
|
|
|
|
|
|
è |
1 5 3ø |
|||||||||
|
æ 1 |
|
2 |
2ö |
|
æ1 |
1 |
|
|
1 |
1ö |
|
|
|
|
|
æ |
1 1 1 1ö |
|||||
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
ç |
|
|
÷ |
|||||
|
ç |
|
|
|
|
÷ |
58. çç1 |
1 |
- 1 - 1÷÷ , |
|
|
|
59. çç0 |
1 |
1 1÷÷ , |
||||||||
57. ç2 |
|
1 - 2÷ , |
|
|
|
||||||||||||||||||
|
ç |
2 |
- 2 |
|
÷ |
|
ç1 - 1 |
|
|
1 |
1÷ |
|
|
|
|
|
ç |
0 0 1 1÷ |
|||||
|
è |
1ø |
|
ç |
- 1 |
- 1 |
÷ |
|
|
|
|
|
ç |
|
|
÷ |
|||||||
|
|
|
|
|
|
|
|
è1 |
1ø |
|
|
|
|
|
è |
0 0 0 1ø |
|||||||
|
æ1 |
1 |
0 |
0ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ç |
|
1 |
1 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60. |
ç0 |
0÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ç |
0 |
0 |
1 |
1 |
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ç |
0 |
0 |
0 |
1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
§4. Системы линейных алгебраических уравнений |
|||||||||||||||||||
|
|
|
Системой линейных алгебраических уравнений, содержащей m |
||||||||||||||||||||
уравнений с n неизвестными, называется система вида |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
ìa x + a x |
|
|
+ K |
+ a |
|
x |
|
|
= b , |
|
|
|||||
|
|
|
|
|
|
|
ï 11 1 |
12 |
2 |
|
|
1n |
|
n |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
ïa21 x1 + a22 x2 + K + a2n xn |
|
= b2 , |
|
(1) |
||||||||||||
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïL L L L L L L L L L L |
|
|
||||||||||||||
|
|
|
|
|
|
|
ïa |
x + a |
m2 |
x |
2 |
+ K + a |
mn |
x |
n |
= b , |
|
|
|||||
|
|
|
|
|
|
|
î |
m1 1 |
|
|
|
|
|
|
m |
|
|
||||||
где |
aij |
– коэффициенты системы (1 £ i £ m ,1 £ j |
£ n ), bi |
– свободные чле- |
|||||||||||||||||||
ны, |
x j |
– неизвестные числа подлежащие определению. |
|
|
|
||||||||||||||||||
|
|
|
Систему (1) можно записать в матричной форме |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
AX = B , |
|
|
|
|
|
|
|
|
(2) |
|||
где A – основная матрица, т.е. матрица, составленная из коэффициентов |
|||||||||||||||||||||||
системы; |
X – |
вектор-столбец из неизвестных x j |
; B |
– |
вектор-столбец из |
||||||||||||||||||
свободных членов bi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Решением системы (1) называется множество из n |
неизвестных x j , |
|||||||||||||||||||
при подстановке которых в систему(1), каждое ее уравнение обращается в тождество.
Остановимся на трех способах решения систем линейных алгебраических уравнений.
Суть первого, который называется методом Крамера, определяется равенствами
10
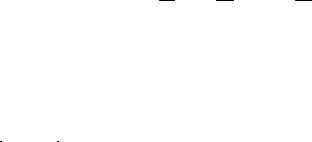
x1 = D1 , x2 = D2 , …, xn = Dn ,
D D D
где x j – неизвестные, D – определитель основной матрицы (определитель системы), D j – определители матриц полученных из основной заменой j -го столбца столбцом свободных членов bi .
Пример 1. Цена обращающихся на рынке акций ,АВ, С, D, их стоимость и ожидаемый доход зависящий от обменного курса приведены в следующей таблице:
Акция |
Текущая |
Ожидаемый доход, если обменный курс |
|||
стоимость |
понизится |
не изменится |
повысится |
||
|
|||||
А |
77 |
60 |
75 |
90 |
|
В |
85 |
100 |
75 |
75 |
|
С |
110 |
95 |
120 |
105 |
|
D |
75 |
50 |
50 |
105 |
|
Составить структуру портфеля и найти доходность.
Решение: Составим портфель из первых трех акций, обеспечивающий такой ожидаемый доход, какой имеет акция D. Структуру данного портфеля найдем как решение системы уравнений:
ì60x1 |
+ 100x2 + 95x3 |
= 50, |
|
ï |
+ 75x2 |
+ 120x3 |
= 50, |
í75x1 |
|||
ï |
+ 75x2 |
+ 105x3 |
= 105. |
î90x1 |
|||
Решение системы проведем методом Крамера. Найдем определитель основной матрицы:
|
60 |
100 |
95 |
|
D = |
75 |
75 |
120 |
= 118125 . |
|
90 |
75 |
105 |
|
Определители матриц полученных из основной заменой j -го столбца
столбцом свободных членов bi соответственно равны:
|
|
50 |
100 |
95 |
|
|
|
|
60 |
50 |
95 |
|
||
D1 |
= |
50 |
75 |
120 |
= 286875 , |
D2 = |
75 |
50 |
120 |
= 25875 , |
||||
|
|
105 |
75 |
105 |
|
|
90 |
105 |
105 |
|
||||
|
|
|
|
60 |
100 |
50 |
|
|
= -146250 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D3 |
= |
|
|
75 |
75 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
90 |
75 |
105 |
|
|
|
|
|
|
|
|
11
|
|
|
Таким |
образом, |
решение системы имеет |
:видx = |
D1 |
» 2,43 , |
||
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
D |
|
|
|
|
|
|
|
|
|
|
||
x |
2 |
= |
D2 |
» 0,22 , x = |
D3 |
» -1,24 . Следовательно, искомая цена будет рав- |
||||
|
|
|||||||||
|
|
D |
3 |
D |
|
|
|
|
||
на 77 × 2,43 + 85 × 0,22 - 110 × 1,24 = 69,4 . Это означает, |
что продав акцию |
|||||||||
D и купив указанный портфель, получим 75 - 69,5 = 5,6 ден. ед. дохода. |
||||||||||
|
|
|
Второй – называют матричным способом или методом обратной |
|||||||
матрицы, и он выражается формулой |
|
|
|
|||||||
|
|
|
|
|
|
|
X = A-1B . |
|
(3) |
|
|
|
|
Последнее равенство получено из равенства(2) умножением слева на |
|||||||
обратную матрицу для основной матрицы системы. |
|
|
|
|||||||
|
|
|
Пример 2. Потребитель тратит 20 руб. в день на апельсины и яблоки. |
|||||||
Предельная полезность яблок для него равна20 - 3x , где x – количество яблок, в шт. Предельная полезность апельсинов равна 40 - 5 y , где y – ко-
личество апельсинов, в шт. Цена одного яблока составляет 1 руб., цена одного апельсина – 5 руб. Какое количество яблок и апельсинов купит рациональный потребитель?
|
|
|
Решение: Так как в состоянии равновесия отношение предельных по- |
|||||||||||||||||||||||||||
лезностей равно отношению цен товаров: |
|
MU x |
|
|
= |
Px |
, а выбор потребите- |
|||||||||||||||||||||||
|
MU y |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Py |
|
|
||||
ля предопределен бюджетным ограничением: |
Px ´ x + Py |
´ y = 1 , то реше- |
||||||||||||||||||||||||||||
ние задачи можно найти как решение системы: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ì20 - 3x |
= |
1 |
|
, |
|
|
|
|
|
|
|
|
|
ì3x - y = 12, |
|
|||||||||
|
|
|
|
|
|
ï |
|
|
|
|
|
|
или, что тоже самое |
|
||||||||||||||||
|
|
|
|
|
|
|
- 5 y |
5 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
í40 |
|
|
|
í |
|
+ 5 y |
= 20. |
|
||||||||||||||||
|
|
|
|
|
|
ï |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
îx |
|
||||||
|
|
|
|
|
|
îx + 5y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Решим |
полученную |
|
систему методом |
обратной матрицы. Основная |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ3 |
- 1ö |
|
|
|
|
|
|
||||
матрица |
|
системы |
|
|
|
|
имеет |
видA = |
ç |
|
|
|
÷ |
, |
|
а |
обратная |
ей– |
||||||||||||
|
|
|
|
|
ç |
|
|
|
÷ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è 1 |
|
5ø |
|
|
|
|
|
|
|||
|
-1 |
|
1 |
æ |
5 |
1ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
= |
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
16 |
ç |
- 1 |
3 |
÷ . Тогда, столбец из неизвестных найдем по формуле (3): |
|
||||||||||||||||||||||||
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
æ x ö |
|
-1 |
|
|
|
|
1 |
æ |
5 1ö |
æ12 ö |
|
1 |
æ |
80ö |
æ5ö |
|
||||||||
|
|
|
|
|
|
ç ÷ |
= A |
B = |
|
ç |
÷ |
ç |
÷ |
= |
ç |
÷ |
ç ÷ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
ç ÷ |
|
|
|
|
× ç |
÷ |
× ç ÷ |
|
|
|
× ç |
÷ |
= ç ÷ . |
|
||||||||||
|
|
|
|
|
|
è y ø |
|
|
|
|
|
|
16 è- 1 3ø è20ø |
|
16 è |
48ø |
è3ø |
|
||||||||||||
|
|
|
Таким образом, |
x = 5 , |
y = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Оба вышеуказанных способа применимы лишь дляневырожденных систем, т.е. для систем, определитель которых отличен от нуля ( D ¹ 0 ).
Более общим методом решения систем, применимым и для случая вы-
рожденных систем ( D = 0 ), является метод Гаусса, который состоит в
12

последовательном исключении неизвестных. При решении методом Гаусса система в результате элементарных преобразований приводится к ступенчатому (в частности треугольному виду), после чего проводится последовательное определение неизвестных. Причем, для приведения системы к ступенчатому виду удобно проводить преобразования надрасширенной мат-
рицей A , т.е. матрицей полученной из основной добавлением столбца свободных членов.
Пример 3. На рынке обращаются три вида акций А, В, С. Их ожидаемая доходность и коэффициент ее реакции на изменение темпа роста ВВП β1 и темпа инфляции β2 представлены таблицей:
Акции |
r |
β1 |
β2 |
А |
11,5 |
1,0 |
0,6 |
В |
10,0 |
1,1 |
0,4 |
С |
12,0 |
1,5 |
0,8 |
Найти доходность безрисковых вложений x1 и премии за риск x2 , x3 . Решение: Ответ на вопрос задачи найдем как решение системы:
|
|
|
|
|
|
|
ìx |
+ x |
|
+ 0,6 x |
|
= |
11,5 , |
|
|
|
||||||
|
|
|
|
|
|
|
ï 1 |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íx1 |
+ 1,1 x2 + 0,4 x3 |
= 10 , |
|
|
|
||||||||||
|
|
|
|
|
|
|
ïx |
+ 1,5 x |
2 |
+ 0,8 x |
3 |
= 12 . |
|
|
|
|||||||
|
|
|
|
|
|
|
î 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Воспользуемся методом Гаусса. Составим расширенную матрицу |
||||||||||||||||||||||
системы |
|
и преобразуем ее к ступенчатому виду: |
|
|
|
|||||||||||||||||
A |
|
|
|
|||||||||||||||||||
æ1 |
1 |
0,6 |
11,5ö |
A - |
A |
æ 1 |
|
|
|
1 |
0,6 |
11,5ö |
A |
- 5A |
||||||||
|
|
ç |
|
|
÷ |
2 |
|
|
|
1 |
ç |
|
|
|
|
|
|
÷ |
3 |
2 |
||
A = ç1 |
1,1 |
0,4 |
10÷ |
|
Þ |
|
|
ç0 |
|
0,1 |
- 0,2 - 1,5÷ |
|
Þ |
|||||||||
ç1 |
1,5 |
0,8 |
12÷ |
A - |
A |
ç |
0 |
|
0,5 |
0,2 |
0,5÷ |
|
|
|||||||||
è |
|
|
ø |
3 |
|
|
|
1 |
è |
|
|
|
|
|
|
ø |
|
|
||||
|
|
|
|
|
|
|
|
æ 1 |
|
|
|
1 |
|
|
0,6 |
11,5ö |
|
|
|
|||
|
|
|
|
|
|
|
|
ç |
|
|
0,1 |
- 0,2 |
÷ |
|
|
|
||||||
|
|
|
|
|
|
|
Þ ç0 |
|
- 1,5÷ . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ç |
0 |
|
|
|
0 |
|
|
1,2 |
÷ |
|
|
|
||
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
8ø |
|
|
|
|||||
Полученной матрице соответствует система треугольного вида:
ìx |
+ x |
|
+ 0,6 x |
= |
11,5 |
, |
|
ï |
1 |
|
2 |
3 |
|
|
|
í |
0,1 x2 |
- 0,2 x3 |
= -1,5 |
, |
|||
ï |
|
|
|
1,2 x3 |
= 8 . |
||
î |
|
|
|
||||
Последовательно находя x3 |
из третьего, x2 из второго и x1 из перво- |
||||||
го уравнения системы, получим: x1 |
» 9,17 , x2 |
» -1,67 , x3 » 6,67 . |
|||||
Рассмотрим теперь некоторые элементарные виды систем и условия их разрешимости.
1. Система двух линейных уравнений с двумя неизвестными
13
ìía11 x1 + a12 x2 = b1 , îa21 x1 + a22 x2 = b2 ,
имеет единственное решение при условии, что D ¹ 0 .
2. Система трех однородных уравнений с тремя неизвестными
ìïa11 x1 + a12 x2 + a13 x3 = 0, ía21 x1 + a22 x2 + a23 x3 = 0, ïîa31 x1 + a32 x2 + a33 x3 = 0
имеет отличные от нуля решения, если D = 0 .
3. Система трех уравнений с тремя неизвестными
ìa x |
+ a x |
|
+ a x |
|
|
= b , |
|||||||
ï |
11 |
1 |
12 |
|
2 |
13 |
|
3 |
1 |
||||
ía21 x1 |
+ a22 x2 + a23 x3 = b2 , |
||||||||||||
ïa |
31 |
x |
+ a |
32 |
x |
2 |
+ a |
33 |
x |
3 |
= b |
||
î |
|
1 |
|
|
|
|
|
3 |
|||||
имеет решение при D ¹ 0 .
4. И в качестве особого случая(число неизвестных больше числа уравнений) – систему двух однородных уравнений с тремя неизвестными
|
|
|
ìa x + a x |
|
+ a x = 0, |
|
|
|
|
|
|||||||||||
|
|
|
í |
11 |
1 |
12 |
2 |
|
13 |
3 |
|
|
|
|
|
|
|
|
|||
|
|
|
îa21 x1 + a22 x2 + a23 x3 = 0, |
|
|
|
|
|
|||||||||||||
решение которой определяется формулами |
|
|
|
|
|
|
|
|
|
||||||||||||
x = k |
|
a12 |
a13 |
|
, |
|
x |
2 |
= - k |
|
a11 |
a13 |
|
, |
x = k |
|
a11 |
a12 |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
a22 |
a23 |
|
|
|
|
|
|
a21 |
a23 |
|
|
3 |
|
a21 |
a22 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где k – произвольное число.
Задания
Методом Крамера решить следующие системы уравнений:
61. |
ì38 x |
- 27 x |
|
= -5, |
62. |
ì11 x |
|
+ 13 x |
|
= 93, |
|
|||||
í |
1 |
|
2 |
= -23, |
í |
|
1 |
|
|
|
2 |
= 34, |
|
|||
|
î17 x1 |
- 19 x2 |
|
î22 x1 |
+ 7 x2 |
|
||||||||||
63. |
íì12 x -13 y = 20, |
64. |
íì19 x - 18 y = 15, |
|
||||||||||||
|
î14 x -17 y = 38, |
|
î2 x + 7 y = 203, |
|
||||||||||||
|
ì21 x - 20 y = 60, |
|
ì2x |
|
+ 7 x |
|
- |
8x = |
3, |
|||||||
65. |
66. |
ï |
1 |
|
|
2 |
|
|
3 |
|
||||||
í |
|
|
|
|
í3x1 + 4x2 - 8x3 = 2, |
|||||||||||
|
î7 x - 6 y = 32, |
|
ï |
|
|
- 3x2 - 3x3 = 10, |
||||||||||
|
|
|
|
|
|
|
î8x1 |
|
||||||||
14
|
ì5x - 2 y + 3z = 4, |
|
ì8x - 3y - 2z = 1, |
|||||||||||||||
67. |
íï3x - 5 y + 7z = 0, |
68. |
íï8x + 9 y - 5z = 7, |
|||||||||||||||
|
ï |
|
|
|
|
|
ï |
|
|
- 2 y |
+ 4z = 13. |
|||||||
|
î4x + 2 y - 5z = 3, |
|
î7x |
|
||||||||||||||
|
|
Методом обратной матрицы решить следующие системы уравнений: |
||||||||||||||||
69. |
ì3 x |
+ 7 x |
|
= 126, |
70. |
ì11 x |
+ 2 x |
|
= -13, |
|||||||||
í |
1 |
|
2 |
= 221, |
í |
|
|
1 |
|
|
|
2 |
= -9, |
|||||
|
î8 x1 |
+ 11 x2 |
|
î13 x1 |
+ 3 x2 |
|||||||||||||
71. |
íì17 x + 19 y = -8, |
72. |
íì11 x + 12 y = 76, |
|||||||||||||||
|
î6 x + 11 y = -20, |
|
î3 x + 2 y = 36, |
|
|
|||||||||||||
|
ì15 x + 2 y = 23, |
|
ì2x |
|
+ 3x |
|
+ |
5x |
|
= 10, |
||||||||
73. |
74. |
ï |
1 |
|
|
|
2 |
|
|
|
3 |
|
||||||
í |
|
|
|
|
í3x1 + 7x2 + 4x3 = 3, |
|||||||||||||
|
î16 x + 5 y = -7, |
|
ïx |
+ 2x |
2 |
+ 2x |
3 |
|
= 3, |
|||||||||
|
|
|
|
|
|
|
î |
1 |
|
|
|
|
|
|
|
|
||
|
ì5x - 6 y + 4z = 3, |
|
ì4x - 3y + 2z = -4, |
|||||||||||||||
75. |
íï3x - 3y + 2z = 2, |
76. |
íï6x - 2 y + 3z = -1, |
|||||||||||||||
|
ï |
|
|
|
|
|
ï |
|
|
- 3y + 2z = -3. |
||||||||
|
î4x - 5y + 2z = 1, |
|
î5x |
|
||||||||||||||
Методом Гаусса решить следующие системы уравнений:
77. |
íìx1 + 4 x2 |
|
= 23, |
78. |
íìx1 |
- 2 x2 |
|
= 17, |
|
|
||||||
|
î2 x1 + 3 x2 |
= -14, |
|
î3 x1 + 8 x2 = -19, |
||||||||||||
79. |
íìx - 3 y = 35, |
80. |
íì2 x + 7 y = 73, |
|
|
|||||||||||
|
î12 x + 11 y = 514, |
|
î3 x + 8 y = 77, |
|
|
|||||||||||
|
ìx + 2 y = 3, |
|
ì2x |
|
+ 7x |
|
|
+ 3x |
|
= 11, |
||||||
81. |
82. |
ï |
1 |
|
|
2 |
|
|
3 |
|
||||||
í |
|
|
|
|
í3x1 + 9x2 |
+ 4x3 = 15, |
||||||||||
|
î14 x - 7 y |
= 7, |
|
ïx |
+ 5x |
2 |
+ 3x |
= 10, |
||||||||
|
|
|
|
|
|
|
î |
1 |
|
|
|
|
3 |
|
|
|
|
ìx + 2 y + 2z = 8, |
|
ì3x - 4 y + 5z = 6, |
|||||||||||||
83. |
íï2x + y - 2z = 1, |
84. |
íï2x - 3y + z = -3, |
|||||||||||||
|
ï |
|
+ z = 4, |
|
ï |
|
|
- 5 y - z = -12. |
||||||||
|
î2x - 2 y |
|
î3x |
|
||||||||||||
|
|
Решить следующие системы уравнений: |
|
|
|
|
|
|||||||||
85. |
ì5 x + 3 x |
|
+ 4 x = 0, |
86. |
ì4 x - 6 x |
|
+ 5 x = 0, |
|||||||||
í |
1 |
|
2 |
3 |
í |
|
1 |
|
|
2 |
|
|
3 |
|||
|
î6 x1 + 5 x2 + 6 x3 = 0, |
|
î6 x1 - 9 x2 + 10 x3 = 0, |
|||||||||||||
15
87. |
ì2 x + 3 x |
|
+ 5 x = 0, |
|
88. |
ì8 x - 5 x |
|
- 6 x |
|
= 0, |
|
|||||||||||||
í |
1 |
|
|
|
2 |
|
3 |
|
|
|
í |
1 |
|
|
2 |
|
|
3 |
|
|
|
|||
|
î3 x1 + 4 x2 + 6 x3 = 0, |
|
|
î4 x1 - x2 - 3 x3 = 0, |
|
|||||||||||||||||||
89. |
ì3 x + 5 y + 6 z = 0, |
|
|
|
90. |
ì- 5 x - 6 y + 3 z = 0, |
|
|||||||||||||||||
í |
+ y |
+ 4 z = 0, |
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
||||||||
|
îx |
|
|
|
|
î- 7 x - 9 y + 5 z = 0. |
|
|||||||||||||||||
|
|
Решить матричные уравнения: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
æ4 5 |
ö |
|
|
|
|
æ19 8 |
ö |
|
|
|
æ |
1 2ö |
|
|
|
æ12 2 |
ö |
|
|||||
91. |
ç |
|
÷ |
× X = |
ç |
÷ |
, |
|
92. |
ç |
|
|
÷ |
X = |
ç |
|
|
÷ |
|
|||||
ç |
|
÷ |
ç |
÷ |
|
ç |
3 7 |
÷ × |
ç |
|
|
÷ , |
|
|||||||||||
|
è0 1 |
ø |
|
|
|
|
è 3 0 |
ø |
|
|
|
è |
ø |
|
|
|
è41 7 |
ø |
|
|||||
|
æ5 3 |
ö |
|
|
|
|
æ10 16ö |
|
|
æ 1 |
|
2 |
- 3ö |
|
|
æ 1 |
- 3 0ö |
|||||||
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
ç |
÷ |
||||||
93. |
ç |
|
÷ |
× X = |
ç |
|
÷ |
, |
94. ç 3 |
|
2 |
- 4÷ × X = ç10 |
2 7 ÷ , |
|||||||||||
ç |
|
÷ |
ç |
|
÷ |
|
||||||||||||||||||
|
è1 0 |
ø |
|
|
|
|
è 2 2 |
ø |
|
|
ç |
2 - 1 |
|
|
0 |
÷ |
|
|
ç |
÷ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
è10 |
7 8ø |
||||
|
|
æ |
|
5 |
|
|
3 |
1ö |
|
|
æ |
- 8 3 0ö |
|
|
|
|
|
|
|
|
|
|
||
95. |
|
ç |
|
1 |
- 3 |
÷ |
|
|
ç |
|
0 |
÷ |
|
|
|
|
|
|
|
|
|
|
||
X × ç |
|
- 2÷ = ç - 5 9 |
÷ . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ç |
|
5 |
|
|
2 |
÷ |
|
|
ç |
- 2 15 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
è- |
|
|
1ø |
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|||||
16
|
Тестовые задания к первой главе |
|
Задание { 1 }. |
Прямоугольная таблица чисел, содержащая m строк одина- |
|
ковой длины или n столбцов одинаковой длины, называется |
||
- : определителем, |
- : матрицей, |
|
- : вектор-столбцом, |
- : единичной матрицей. |
|
Задание { 2 }. |
Числа aij , составляющие матрицу, называются ее |
|
- : постоянными, |
|
- : коэффициентами, |
- : элементами, |
|
- : слагаемыми. |
Задание { 3 }. Две матрицы называются равными, если равны их |
||
- : все соответствующие элементы, |
- : определители, |
|
- : канонические матрицы, |
- : размеры. |
|
Задание { 4 }. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется
- : единичной, |
|
- : диагональной, |
- : транспонированной, |
- : треугольной. |
|
Задание { 5 }. |
Диагональная матрица называется единичной, если все эле- |
|
менты главной диагонали |
|
|
- : равны между собой, |
- : равны нулю, |
|
- : равны числу e , |
- : равны единице. |
|
Задание { 6 }. |
Если все элементы матрицы, расположенные по одну сторо- |
|
ну от главной диагонали равны нулю, то матрица называется |
||
- : треугольной, |
|
- : диагональной, |
- : транспонированной, |
- : единичной. |
|
Задание { 7 }. |
Матрица, |
полученная из данной заменой каждой ее строки |
столбцом с тем же номером, называется по отношению к данной |
||
- : обратной, |
|
- : транспонированной, |
- : присоединенной, |
- : единичной. |
|
Задание { 8 }. |
Матрица - A = (- 1)A по отношению к матрице A называется |
|
- : обратной, |
|
- : отрицательной, |
- : противоположной, |
- : присоединенной. |
|
Задание { 9 }. |
Матрицы, |
которые могут быть получены одна из другой в |
результате элементарных преобразований называются |
||
- : равными, |
|
- : обратными, |
- : транспонированными, |
- : эквивалентными. |
|
Задание { 10 }. |
Матрица, |
у которой в начале главной диагонали стоят под- |
ряд несколько единиц, а все остальные элементы равны нулю, называется |
||
- : треугольной, |
|
- : канонической, |
- : единичной, |
|
- : нулевой. |
Задание { 11 }. |
Квадратная матрица, определитель которой отличен от нуля |
|
называется |
|
|
- : невырожденной, |
- : канонической, |
|
- : транспонированной, |
- : ненулевой. |
|
17
Задание { 12 }. Если определитель квадратной матрице равен нулю, то такая
матрица называется |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- : невырожденной, |
|
|
|
|
- : союзной, |
|
|
|
|
|
|||||||
- : вырожденной, |
|
|
|
|
- : нулевой. |
|
|
|
|
|
|||||||
Задание { 13 }. |
Наибольший |
из порядков |
миноров исходной |
матрицы, от- |
|||||||||||||
личных от нуля, называется ее |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- : определителем, |
|
|
|
|
- : алгебраическим дополнением, |
|
|||||||||||
- : базисом, |
|
|
|
|
|
- : рангом. |
|
|
|
|
|
||||||
Задание { 14 }. |
Матрица |
системы |
|
алгебраических |
уравнений |
дополненная |
|||||||||||
столбцом свободных членов называется |
|
|
|
|
|
|
|
|
|
||||||||
- : основной, |
|
|
|
|
|
- : расширенной, |
|
|
|
|
|||||||
- : совместной, |
|
|
|
|
|
- : увеличенной. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
æ |
12 - 1 0 ö |
æ- 11 2 |
|
1 ö |
|
||||
Задание { 15 }. |
Суммой |
двух |
|
|
ç |
|
|
|
÷ |
ç |
|
|
÷ |
яв- |
|||
матриц ç |
|
|
|
÷ |
и ç |
- 4 |
÷ |
||||||||||
ляется матрица |
|
|
|
|
è |
- 10 5 2 ø |
è 11 |
- 1ø |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
æ |
23 |
3 |
1ö |
|
|
|
æ1 |
3 |
1ö |
|
|
|
|
|
|
||
ç |
|
|
÷ |
|
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
|
|
÷ , |
|
|
ç |
|
|
|
÷ , |
|
|
|
|
|
|
|
è |
21 9 3ø |
|
|
|
è1 - 1 3ø |
|
|
|
|
|
|
||||||
æ1 1 1ö |
|
|
|
æ23 - 3 1ö |
|
|
|
|
|
|
|||||||
ç |
|
|
÷ |
|
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
|
|
÷ , |
|
|
ç |
1 |
|
|
÷ . |
|
|
|
|
|
|
|
è1 1 1ø |
|
|
|
è |
|
- 9 1ø |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
æ2 |
3 |
1 ö |
|
|
|
|
|
Задание { 16 }. |
Произведением матрицы |
ç |
|
÷ |
на число k = 3 |
являет- |
|||||||||||
ç |
9 |
÷ |
|||||||||||||||
ся матрица |
|
|
|
|
|
|
è5 |
7 ø |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
æ |
6 |
9 |
3 ö |
|
|
|
æ |
6 |
3 |
1ö |
|
|
|
|
|
|
|
ç |
|
|
÷ |
, |
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
|
27 |
÷ |
|
ç |
5 |
9 |
|
÷ , |
|
|
|
|
|
|
||
è15 |
21ø |
|
|
|
è |
7ø |
|
|
|
|
|
|
|||||
æ |
6 |
9 |
3ö |
|
|
|
æ 2 |
|
3 |
1 ö |
|
|
|
|
|
|
|
ç |
|
|
÷ |
|
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
5 |
9 |
÷ , |
|
|
ç |
|
27 |
÷ . |
|
|
|
|
|
|||
è |
7ø |
|
|
|
è15 |
21ø |
|
|
|
|
|
|
|||||
|
|
|
|
|
æ0 - 1 ö |
|
|
æ- 3 - 3ö |
|
|
|
|
|
||||
Задание { 17 }. |
|
ç |
÷ |
B |
|
ç |
|
÷ |
, то значение |
выраже- |
|||||||
Если A = ç |
÷ , |
= ç |
|
÷ |
|||||||||||||
ния A - B равно |
è2 |
- 4ø |
|
|
è- 5 - 5ø |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
æ |
3 |
2ö |
|
|
|
|
æ |
0 |
|
3 ö |
|
|
|
|
|
|
|
ç |
|
÷ |
|
|
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
7 |
÷ , |
|
|
ç |
- 10 |
- |
÷ , |
|
|
|
|
|
|
|||
è |
1ø |
|
|
|
|
è |
9ø |
|
|
|
|
|
|
||||
æ |
- 3 - 4ö |
|
|
|
æ 3 - 3ö |
|
|
|
|
|
|
||||||
ç |
|
|
÷ |
|
|
- : |
ç |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
3 |
- |
÷ , |
|
|
ç |
- 3 |
|
1 |
÷ . |
|
|
|
|
|
|
|
è |
9ø |
|
|
|
è |
|
ø |
|
|
|
|
|
|
||||
18
Задание { 18 }.
æ 9 |
- 8 |
|
ö |
|
||
ç |
|
|
|
|
÷ |
, |
- : ç |
|
- 20 |
÷ |
|||
è10 |
ø |
|
||||
æ0 |
- 6 |
ö |
|
|
|
|
ç |
|
|
÷ |
, |
|
|
- : ç |
3 |
- 9 |
÷ |
|
|
|
è |
ø |
|
|
|
||
Задание { 19 }.
читься
-: единичная,
-: треугольная,
Задание { 20 }.
матрица
æ2 |
- 1 |
ö |
|
|||
ç |
|
|
|
|
÷ |
, |
- : ç |
3 |
- 2 |
÷ |
|||
è |
ø |
|
||||
æ1 |
0 |
ö |
|
|
|
|
ç |
|
|
÷ |
, |
|
|
- : ç |
0 |
1 |
÷ |
|
|
|
è |
ø |
|
|
|
||
Произведение матриц |
A = |
æ |
3 |
- 2ö |
|
на |
B = |
æ |
3 |
4ö |
равно |
|||
ç |
|
|
|
÷ |
|
ç |
|
÷ |
||||||
|
|
|
ç |
5 |
- |
4 |
÷ |
|
|
|
ç |
2 |
÷ |
|
|
|
|
è |
ø |
|
|
|
è |
5ø |
|
||||
æ6 |
2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
÷ |
, |
|
|
|
|
|
|
|
|
|
|
|
- : ç |
1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
è7 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
æ5 |
2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
- : ç |
0 |
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
è7 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ2 |
|
- 3ö |
æ9 |
- 6ö |
|
|
|
|
||||
При умножении матриц |
ç |
|
|
|
÷ |
× |
ç |
|
÷ |
|
матрица полу- |
|||
ç |
4 |
|
- 6 |
÷ |
ç |
6 |
÷ |
|
||||||
|
|
è |
|
ø |
|
è |
- 4ø |
|
|
|
|
|||
-: нулевая,
-: диагональная.
|
|
|
æ2 |
- 1 ö |
|
||
|
|
|
ç |
|
|
÷ |
в квадрат получится |
При возведении матрицыç |
3 |
- 2 |
÷ |
||||
|
|
|
è |
ø |
|
||
æ |
0 |
1ö |
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
|
- : ç |
1 |
÷ , |
|
|
|
|
|
è |
0ø |
|
|
|
|
|
|
æ16 |
1 ö |
|
|
|
|
||
ç |
|
|
÷ |
|
|
|
|
- : ç |
81 |
16 |
÷ . |
|
|
|
|
è |
ø |
|
|
|
|
||
æ1 |
- 2ö |
|
||
ç |
|
|
÷ |
в квадрат получится |
Задание { 21 }. При возведении матрицыç |
3 |
- 4 |
÷ |
|
è |
ø |
|
||
матрица
æ |
- 5 |
|
|
6 ö |
|
|
|
|
æ1 |
0 |
ö |
|
|
|
|
||||
ç |
|
|
|
|
|
|
÷ |
, |
|
|
|
ç |
|
|
÷ |
, |
|
|
|
- : ç |
- 9 |
|
10 |
÷ |
|
|
|
- : ç |
0 |
1 |
÷ |
|
|
|
|||||
è |
|
ø |
|
|
|
|
è |
ø |
|
|
|
|
|||||||
æ |
1 |
|
4 ö |
|
|
|
|
|
|
æ - 1 |
2ö |
|
|
||||||
ç |
|
|
|
÷ |
, |
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
- : ç |
9 |
|
|
÷ |
|
|
|
|
|
- : ç |
- 6 |
3 |
÷ . |
|
|||||
è |
16ø |
|
|
|
|
|
|
è |
ø |
|
|
||||||||
|
|
|
|
|
|
|
|
|
æ1 |
1ö |
|
|
æ1 |
|
0ö |
2 |
|||
Задание { 22 }. Если |
ç |
|
÷ |
|
|
ç |
|
|
|
÷ |
, то выражение A - E равно |
||||||||
A = ç |
0 |
÷ |
, E = ç |
|
|
1 |
÷ |
||||||||||||
|
|
|
|
|
|
|
|
|
è |
1ø |
|
|
è0 |
|
ø |
|
|||
æ |
2 |
|
2ö |
|
|
|
|
|
|
|
æ0 |
2 |
ö |
|
|
|
|
||
ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
ç |
|
|
÷ |
, |
|
|
|
- : ç |
0 |
|
2 |
÷ |
|
|
|
|
|
|
- : ç |
0 |
0 |
÷ |
|
|
|
||
è |
|
ø |
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
||||
æ |
0 |
|
0ö |
|
|
|
|
|
|
|
æ |
0 |
2 |
ö |
|
|
|
|
|
ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
ç |
|
|
÷ |
|
|
|
|
- : ç |
2 |
|
0 |
÷ |
|
|
|
|
|
|
- : ç |
2 |
0 |
÷ . |
|
|
|||
è |
|
ø |
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
||||
19

Задание { 23 }.
æ3 |
1 |
ö |
|
|
ç |
|
|
÷ |
, |
- : ç |
0 |
3 |
÷ |
|
è |
ø |
|
||
æ4 |
0 |
ö |
|
|
ç |
|
|
÷ |
, |
- : ç |
0 |
4 |
÷ |
|
è |
ø |
|
||
Задание { 24 }.
æ- 2 |
- 11ö |
|
||
ç |
|
|
÷ |
, |
- : ç |
- 1 |
|
÷ |
|
è |
- 5 ø |
|
||
æ- 5 |
11 |
ö |
|
|
ç |
|
|
÷ |
|
- : ç |
1 |
- 2 |
÷ , |
|
è |
ø |
|
||
Задание { 25 }.
æ 13 |
|
0 |
ö |
|
||
ç |
|
|
|
÷ |
|
|
- : ç |
|
|
- 3 |
÷ , |
|
|
è13 |
|
ø |
|
|||
æ - |
3 |
0 |
ö |
|
||
ç |
|
|
1 |
|
÷ |
, |
- : ç |
- 13 |
|
÷ |
|||
è |
3 |
ø |
|
|||
Если |
æ2 |
1 ö |
= |
|
æ1 |
|
0ö |
, то выражение A2 + E равно |
||||
A = ç |
|
÷ , E |
|
ç |
|
|
÷ |
|||||
|
ç |
2 |
÷ |
|
|
ç |
|
|
÷ |
|
|
|
|
è0 |
ø |
|
|
è0 |
|
1ø |
|
|
|
||
|
|
|
æ |
7 |
|
0ö |
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
|
- : ç |
4 |
|
7 |
÷ |
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
||
|
|
|
æ5 |
|
4ö |
|
|
|
|
|
||
|
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
- : ç |
0 |
|
5 |
÷ . |
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
||
|
|
|
|
|
|
æ2 |
|
11ö |
|
|
||
Обратной для матрицы |
ç |
|
|
|
÷ |
является матрица |
||||||
ç |
|
|
5 |
÷ |
||||||||
|
|
|
|
|
|
è1 |
|
ø |
|
|
||
|
|
|
æ |
2 |
|
1ö |
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
, |
|
|
|
|
|
|
|
- : ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
è11 |
|
5ø |
|
|
|
|
|
||
|
|
|
æ- 2 |
- 1ö |
|
|
|
|||||
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
11 |
|
5 |
÷ . |
|
|
|||
|
|
|
è |
|
ø |
|
|
|
||||
|
|
|
|
|
|
æ 3 |
|
|
0 |
ö |
|
|
Обратной для матрицы |
ç |
|
|
- 1 |
÷ |
является матрица |
||||||
ç13 |
÷ |
|||||||||||
|
|
|
|
|
|
è |
|
|
|
|
3 ø |
|
|
|
|
æ3 |
|
13 ö |
|
|
|
||||
|
|
|
ç |
|
|
|
1 |
|
÷ |
|
|
|
|
|
|
- : ç |
0 |
|
- |
3 |
÷ , |
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|||
|
|
|
æ |
0 |
|
|
3 ö |
|
|
|
||
|
|
|
ç |
|
1 |
|
|
|
÷ |
|
|
|
|
|
|
- : ç |
- |
3 |
|
|
÷ . |
|
|
||
|
|
|
è |
|
13ø |
|
|
|
||||
|
|
|
|
|
|
|
|
|
æ |
7 |
11ö |
|
||
Задание { 26 }. |
Обратной для матрицы |
ç |
|
|
÷ |
является матрица |
||||||||
ç |
5 |
|
÷ |
|||||||||||
|
|
|
|
|
|
|
|
|
è |
8 ø |
|
|||
æ 7 |
5ö |
|
|
|
æ- 7 |
|
11 ö |
|
|
|||||
ç |
|
|
÷ |
, |
|
|
ç |
|
|
|
|
÷ |
, |
|
- : ç |
|
8 |
÷ |
|
|
- : ç |
5 |
|
- |
8 |
÷ |
|
||
è11 |
ø |
|
|
|
è |
|
ø |
|
|
|||||
æ8 |
11ö |
|
|
|
æ |
8 |
|
- 11ö |
|
|||||
ç |
|
|
÷ |
, |
|
|
ç |
|
|
|
|
÷ |
|
|
- : ç |
5 |
7 |
÷ |
|
|
- : ç |
- 5 |
|
7 |
÷ . |
||||
è |
ø |
|
|
|
è |
|
ø |
|
||||||
|
|
|
|
|
|
|
|
|
æ |
7 |
5ö |
|
|
|
Задание { 27 }. |
Обратной для матрицы |
ç |
|
|
÷ |
|
является матрица |
|||||||
ç |
3 |
|
÷ |
|
||||||||||
|
|
|
|
|
|
|
|
|
è |
2ø |
|
|
||
æ |
7 |
3ö |
|
|
|
æ- 2 |
5 ö |
|
|
|||||
ç |
|
÷ |
, |
|
|
ç |
|
|
|
|
÷ |
, |
|
|
- : ç |
5 |
÷ |
|
|
- : ç |
3 |
|
- |
7 |
÷ |
|
|||
è |
2ø |
|
|
|
è |
|
ø |
|
|
|||||
æ |
2 |
|
- 5ö |
|
æ |
2 |
5ö |
|
|
|
|
|||
ç |
|
|
|
|
÷ |
, |
ç |
|
|
÷ |
|
|
|
|
- : ç |
- 3 |
7 |
÷ |
- : ç |
3 |
|
÷ . |
|
|
|
|
|||
è |
ø |
|
è |
7ø |
|
|
|
|
||||||
20
