Построение обратной допускает матрица

Задание { 29 }. Построение обратной допускает матрица

Задание { 30 }. Построение обратной допускает матрица

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лесев.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

916.62 Кб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

							æ1	1ö
Задание { 28 }.				Обратной для матрицы			ç	÷
Задание { 28 }.				Обратной для матрицы			ç	÷ является матрица
							è0	1ø
- : единичная,					- : вырожденная,
- : невырожденная,					- : диагональная.
Задание { 29 }. Построение обратной допускает матрица
æ 1		2 3ö			æ- 1 9 1 ö
ç				÷	ç			÷
- : ç 7		0 9 ÷ ,			- : ç 0 10 0 ÷ ,
ç	- 2	-		÷	ç	1 1		÷
è	- 2	-	4 6 ø		è	1 1		- 1ø
æ	2	2	8 ö		æ	7	5	10 ö
ç				÷	ç			÷
- : ç 1		0 - 2÷ ,			- : ç1 4			8 ÷ .
ç	- 1	- 1 -		÷	ç	2 - 3		÷
è	- 1	- 1 -		4ø	è	2 - 3		- 6ø
Задание { 30 }. Построение обратной допускает матрица
æ	22	2	12ö		æ	2	3	1ö
ç				÷	ç			÷
- : ç 7 - 1 13÷ ,					- : ç0 4 5÷ ,
ç	11	1	6	÷	ç	1	1	÷
è	11	1	6	ø	è	1	1	1ø
æ- 2 2				4 ö	æ 5			10 15 ö
ç				÷	ç			÷
- : ç 1 - 1 - 2÷ ,					- : ç- 10 - 20 12 ÷ .
ç	3	-		÷	ç	7		÷
è	3	-	3 10 ø		è	7		14 21ø

	æ22	0		2		12ö
Задание { 31 }.	ç	0		- 1			÷
Задание { 31 }.	Ранг матрицы ç 7	0		- 1		13÷ равен
	ç	0		1		6	÷
	è11	0		1		6	ø
- : 4,	- : 1,
- : 3,	- : 2.
	æ2	3	0	1ö
Задание { 32 }.	ç	4	0		÷	равен
Задание { 32 }.	Ранг матрицы ç0	4	0	5÷		равен
	ç	1	0	1	÷
	è1	1	0	1	ø
- : 1,	- : 2,
- : 3,	- : 4.
	æ2	3		1		2ö
Задание { 33 }.	ç	2	- 1			÷	равен
Задание { 33 }.	Ранг матрицы ç0	2	- 1			1÷	равен
	ç	0		5		÷
	è4	0		5		1ø
- : 4,	- : 3,
- : 2,	- : 1.

Задание { 34 }.

-: 4,

-: 2,

Задание { 35 }.

рица

æ0		1	ö
ç		2	÷
- : ç1		2	÷ ,
ç	2	0	÷
è	2	0	ø
æ0		1	2ö
ç				÷	,
- : ç	1	2 0		÷	,
è	1	2 0		ø

Задание { 36 }.

матрица

æ- 2		- 3ö
- : çç	3	3	÷÷ ,
ç	2	3	÷
è			ø
æ- 3		- 2ö
ç	3	3	÷
- : ç			÷ ,
ç	3	2	÷
è			ø

Задание { 37 }.

рица

æ5		0	ö
ç			÷
- : ç4		- 1÷ ,
ç	5	5	÷
è	5	5	ø
æ0		- 1	5ö
ç				÷	,
- : ç	5	4	5	÷	,
è	5	4	5	ø

æ 6

- 8

4ö

- 4

Ранг матрицы ç 3

2÷ равен

- 16

è12

- : 3,

- : 1.

æ1

0 ö

Транспонированной

для

является мат-

матрицы ç

è0

2ø

0ö

- : ç2

1÷ ,

0 ö

- : ç

÷ .

æ - 3

3ö

Транспонированной

для

является

матрицыç

- 2

2ø

- 2

2ö

- : ç

- 3

÷ ,

- 3ö

- : ç

- 2

÷ .

æ5

5ö

Транспонированной для матрицы

является мат-

- 1

è0

5ø

5ö

- : ç- 1

4÷ ,

- 1

5ö

- : ç

÷ .

0ø

æ10

- 1ö

Задание { 38 }.

Транспонированной

для

является

матрицыç

матрица

è 0

10 ø

10 ö

æ 0

- 1ö

- : ç10 0 ÷ ,

- : ç

÷ ,

è10

10 ø

è10

- 1ø

- 1

10ö

æ 10

0 ö

- : ç 0 10÷ .

- : ç

0 ø

- 1 10ø

æ12

24ö

Задание { 39 }.

Союзной к матрице

÷ является матрица

12 ø

6 ö

æ 12

- 24ö

- : ç

- 6

÷ ,

12ø

12 ø

12ö

- 12ö

- : ç

- 12

÷ .

6 ø

æ1

0ö

Задание { 40 }.

Союзной к матрице

является матрица

0ø

- 1 - 2ö

- 1 0ö

0 0ö

- 2 1ö

- :

- : ç

÷ ,

- : ç

÷ ,

- 2 1

÷ ,

- : ç

0 0

÷ .

- 2 0ø

æ - 10

27ö

Задание { 41 }.

Союзной к матрице

является матрица

- 20

54 ø

- 27ö

æ- 10

- 27ö

- : ç

÷ ,

- : ç

- 10 ø

54ø

27ö

æ - 10

20ö

- : ç

- 20

÷ ,

- : ç

- 27

÷ .

10ø

54ø

æ- 112

- 124ö

Задание { 42 }.

Союзной к матрице

- 56

- 62

÷ является матрица

112

-124ö

æ- 112

- 56ö

- : ç

- 56

÷ ,

- : ç

124

62ø

56ö

æ- 62

124ö

- : ç

- 124

- 112

÷ ,

- : ç

- 112

÷ .

		3		- 2					1
Задание { 43 }.	Величина определителя	- 2			1				3		равна:
		2			0	- 2
- : 10,	- : 15,
- : 17,	- : –12.
Задание { 44 }.	Величина определителя	1	2		0			равна:
		1	2		0
		0	1		3
		5	0		- 1
- : 13,	- : 19,
- : –10,	- : 29.
Задание { 45 }.	Величина определителя	2		0	5					равна:
		2		0	5
		1		3	16
		0	- 1		10
- : 87,	- : 78,
- : 17,	- : 19.
Задание { 46 }.	Величина определителя	2		- 1		3				равна:
		2		- 1		3
		- 2			3	2
		0			2	5
- : –1,	- : 0,
- : 9,	- : 11.
Задание { 47 }.	Величина определителя	2	1		10			равна:
		2	1		10
		1	0		3
		0	5		- 1
- : 0,	- : 13,
- : 21,	- : 7.
Задание { 48 }.	Величина определителя	1	1	17			равна:
		1	1	17
		2	2	15
		3	3		9
- : 15,	- : 41,
- : 58,	- : 0.
Задание { 49 }.	Величина определителя	2		3	4				равна:
		2		3	4
		5	- 2		1
		1		2	3
- : 14,	- : –10,
- : 17,	- : 12.

					1	17		- 7
Задание { 50 }.	Величина определителя				- 1	13		1		равна:
					1	7		1
- : 18,	- : 19,
- : 180,		- : –15.
Задание { 51 }.	Величина определителя				2	0		5	равна:
					2	0		5
					1	3	16
					0	- 1	10
- : 87,	- : 13,
- : –5,	- : 16.
Задание { 52 }.	Величина определителя				1		2	4		равна:
					1		2	4
					- 2		1	- 3
					3	- 4		2
- : 11,		- : –9,
- : 0,	- : 5.
Задание { 53 }.	Определитель	2	1	3	равен 40 при l равном
		2	1	3
		l	3	2
		1	4	3

- : 1,		- : 4,
- : 5,		- : 2.
Задание { 54 }.	Определитель		- l		2	1		равен –3 при l равном
			- l		2	1
			2		5	3
			3		4	2
- : -3,		- : 3,
- : 1,		- : -1.
Задание { 55 }.	Определитель		4	- 3			5		равен 100 при l равном
			4	- 3			5
			3	- l			8
			1	- 7		- 5
- : 1,		- : 2,
- : 3,		- : 4.
Задание { 56 }.	Определитель		1	1		1	равен 1 при l равном
			1	1		1
			1	2		3
			1	3	2l
- : 4,		- : 3,
- : 2,		- : 1.

Задание { 57 }.

Определитель

равен 4 при l равном

- : 9,

- : 6,

- : 3,

- : 1.

Задание { 58 }.

Определитель

равен 6 при l равном

- : 5,

- : 6,

- : 7,

- : 8.

Задание { 59 }.

Определитель

равен 20 при l равном

- : 7,

- : 6,

- : 5,

- : 4.

Задание { 60 }.

Метод

Крамера,

при

решение системыíì- x + 2 y = -11,

дает следующий результат:

î7x + 5 y = 1,

- : (3;-4),

- : (4;-3),

- : (3;4),

- : (-4;-3).

Задание { 61 }.

Метод

Крамера, при

решение

системы íì3x + 2 y = 3,

дает

следующий результат:

î5x + 3y = 4,

- : (1;-3),

- : (-1;3),

- : (3;-1),

- : (-3;1).

Задание { 62 }.

Метод

Крамера,

при

решение

системы íì- 7 x + 2 y = -16,

дает следующий результат:

î8x + 7 y = 9,

- : (-2;-1),

- : (-2;1),

- : (2;-1),

- : (2;1).

Задание { 63 }.

ì35x - 9 y = -1,

дает

Метод Крамера, при решение системы í

следующий результат:

î10x - 2 y = 2,

- : (1;1),

- : (1;2),

- : (1;3),

- : (1;4).

Задание { 64 }.	Метод Крамера, при решение системы íì13x + 10 y = -6, дает
	î11x + 9 y = -4,
следующий результат:
- : (-2;2),	- : (-2;-2),
- : (2;2),	- : (2;-2).

Задание { 65 }.	Метод Крамера, при решение системы íì12x + 8 y = -4,
	î6x + 5y = 2,
следующий результат:
- : (4;-3),	- : (-4;3),
- : (-3;4),	- : (3;-4).
Задание { 66 }.	Метод Крамера, при решение системы íì3x - 4 y = 3,
	î5x - 7 y = 6,
следующий результат:
- : (-3;3),	- : (-3;-3),
- : (3;3),	- : (3;-3).
Задание { 67 }.	Метод обратной матрицы для системыíì5x - 5 y = -5,
	î6x - 7 y = -11,
следующий результат:
- : (1;5),	- : (2;5),
- : (3;5),	- : (4;5).

дает

Задание { 68 }.	Метод обратной матрицы для системыíì3x + 3y = -6,	дает
	î7x + 8 y = -9,
следующий результат:
- : (-7;5),	- : (-7;4),
- : (-7;3),	- : (-7;2).
Задание { 69 }.	ì- 3x + 8y = 19,
Задание { 69 }.	Метод обратной матрицы для системыí	= -9,
	î- 7x + 8 y	= -9,
дает следующий результат:
- : (5;7),	- : (7;5),
- : (-5;7),	- : (-7;5).
Задание { 70 }.	Метод обратной матрицы для системы íì15x + 2 y = 3,	дает
	î19x + 5y = 26,
следующий результат:
- : (-4;9),	- : (-3;9),
- : (-2;9),	- : (-1;9).

Задание { 71 }.

Метод обратной матрицы для системыíì13x + 3y = 7,

дает

следующий результат:

î6x + y = -1,

- : (0;9),

- : (-1;10),

- : (-2;11),

- : (-3;12).

Задание { 72 }.

Метод

обратной

матрицы

для

ì12x + 13y = -7,

системыí

+ 9 y = -15,

дает следующий результат:

î10x

- : (-6;5),

- : (-5;6),

- : (5;6),

- : (6;5).

Задание { 73 }.

Метод обратной матрицы

для системыíì7x + 22 y = -78,

дает следующий результат:

î13x + 15y = -119,

- : (8;1),

- : (-8;-1),

- : (-8;1),

- : (8;-1).

Задание { 74 }.

Решение

матричного

- 27 ö

- 5 ö

уравненияç

÷ × X = ç

- 19

имеет следующий вид:

- 23ø

2ö

3ö

- : X =

- :

X =

÷ ,

4ø

4ö

2ö

- : X =

- :

X =

÷ .

2ø

æ11

13ö

æ93ö

Задание { 75 }.

Решение

имеет

матричного уравнения ç

÷ × X

следующий вид:

34ø

8ö

1 ö

- : X =

- :

X =

1ø

- 1ö

8 ö

- : X =

- :

X =

÷ ,

÷ .

1ø

æ12

- 13ö

20ö

Задание { 76 }.

име-

Решение матричного уравнения ç

÷ × X =

ет следующий вид:

è14

- 17 ø

38ø

- 7 ö

- 8ö

- : X =

- :

X =

÷ ,

- 8 ø

5ø

- :

- 5ö

- : X =

- 7 ö

X = ç

÷ ,

÷ .

- 7 ø

9 ø

æ19

- 18ö

15 ö

Задание { 77 }.

Решение

матричного

X =

уравнения

имеет следующий вид:

203ø

æ19ö

21ö

- :

- : X =

X = ç ÷

÷ ,

21ø

23ø

- :

- : X =

25ö

X = ç ÷

÷ .

27 ø

æ21

- 20ö

æ60

Задание { 78 }.

Решение матричного уравнения

име-

÷ × X

ет следующий вид:

6 ø

è32

- :

24ö

- : X =

æ22ö

X = ç ÷

÷ ,

22ø

è20

- :

20ö

- : X =

æ18ö

X = ç

÷ .

è16ø

Задание { 79 }.

Решение

матричного

æ1

2ö

× X =

æ3

5ö

имеет

уравненияç

следующий вид:

9ø

- 1

- 1ö

3 ö

- :

- : X =

X = ç

- 1 - 1ø

6 ö

- 1

- 1ö

- :

- : X =

X = ç

- 1

÷ .

- 1ø

æ2

æ30

35ö

Задание { 80 }.

Решение матричного уравнения

X =

име-

ет следующий вид:

è3

è35

- :

1 ö

- : X =

0ö

X = ç

÷ ,

4ø

- :

5 ö

- : X =

1ö

X = ç

÷ .

4ø

æ8		4	ö	× X	æ16		20ö		име-
Задание { 81 }. Решение матричного уравнения ç			÷	× X	= ç			÷	име-
ç	1	3	÷		ç	2	10	÷
è	1	3	ø		è	2	10	ø

ет следующий вид:

	æ2		1	ö			æ0		3	ö
- :	ç			÷	,	- :	ç			÷	,
- :	X = ç	0	3	÷	,	- :	X = ç	2	1	÷	,
	è	0	3	ø			è	2	1	ø
	æ2		0	ö			æ1		3	ö
- :	ç			÷	,	- :	ç			÷
- :	X = ç	1	3	÷	,	- :	X = ç	2	0	÷ .
	è	1	3	ø			è	2	0	ø

		æa 5ö		æ	1 - 3ö				æ2 4 ö
Задание { 82 }.	В	ç	÷	ç			÷		ç	÷
Задание { 82 }.	В	выражении ç	÷	× ç			÷	= ç		÷ , постоянные a, b
равны		è	4 b ø è		0 2 ø				è4 2 ø
равны			- : a = 2, b = -7 ,
- : a = -2, b = -7 ,			- : a = 2, b = -7 ,
- : a = 2, b = 7 ,			- : a = -2, b = 7 .
			æ a 9		ö		æ2 0ö		æ	25 45ö
Задание { 83 }.	В		ç		÷	×	ç	÷	ç		÷
Задание { 83 }.	В	выражении ç			÷	×	ç	÷	= ç		÷ , постоянные
			è- 1 b		ø		è1 5ø		è	1 15 ø
a, b равны
- : a = -8, b = -3 ,			- : a = 8, b = 3 ,
- : a = -8, b = 3 ,			- : a = 8, b = -3 .
		æa 3ö æ				2 4ö			æ7 11ö
Задание { 84 }.		ç	÷	ç			÷	=	ç	÷
Задание { 84 }.	В выражении ç		÷	× ç			÷	=	ç	÷ , постоянные a, b
равны		è	1 b ø è		-	1 3ø			è2 4ø
равны
- : a = 8, b = 0 ,			- : a = 7, b = 0 ,
- : a = 6, b = 0 ,			- : a = 5, b = 0 .
		æa 5ö æ			3 0ö				æ13 10ö
Задание { 85 }.		ç	÷	ç			÷		ç	÷	, постоянные a, b
Задание { 85 }.	В выражении ç		÷ × ç				÷ =		ç	÷	, постоянные a, b
равны		è8 b ø è- 1 2ø							è17 14ø
равны
- : a = 6, b = 7 ,			- : a = 6, b = 6 ,
- : a = 8, b = 7 ,			- : a = 8, b = 8 .
		æa 7ö		æ1 4ö				æ- 1 31 ö
Задание { 86 }.		ç	÷	ç			÷	ç		÷	, постоянные a, b
Задание { 86 }.	В выражении ç		÷ × ç				÷ =	ç		÷	, постоянные a, b
равны		è 2 b ø è0 5 ø						è	2 - 7 ø
равны			- : a = -1, b = -3 ,
- : a = 1, b = 3 ,			- : a = -1, b = -3 ,
- : a = -1, b = 3 ,			- : a = 1, b = -3 .

Задание { 87 }.

выражении

æa - 2ö

æ1 2ö

æ0 12

, постоянные a, b

× ç

4 b

1 8

равны

è3 0ø

- : a = 6, b = 1,

- : a = -6, b = -1 ,

- : a = -6, b = 1 ,

- : a = 6, b = -1.

æa 2

æ4 5

æ- 12

- 13ö

Задание { 88 }.

выражении

, постоянные

÷ × ç

è1 b

ø è0 1

6 ø

a, b равны

- : a = -3, b = 1 ,

- : a = 3, b = -1 ,

- : a = -3, b = -1 ,

- : a = 3, b = 1 .

ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА

§1. Сложение векторов. Умножение вектора на скаляр

Вектором называется направленный прямолинейный отрезокAB , в котором точка A рассматривается как начало, а точка B – как конец. Вектор

обозначается или указанием его начала и конца AB со стрелкой наверху, или

длина которого равна нулю, называется нулевым и направления не имеет. Если длина вектора равна единице, то такой вектор называется единичным.

Векторы, параллельные одной прямой или лежащие на одной прямой, называются коллинеарными. Векторы, параллельные одной плоскости, или лежащие в одной плоскости называются компланарными. Два коллинеарных вектора имеющих равные длины и одно направление, называются равными.

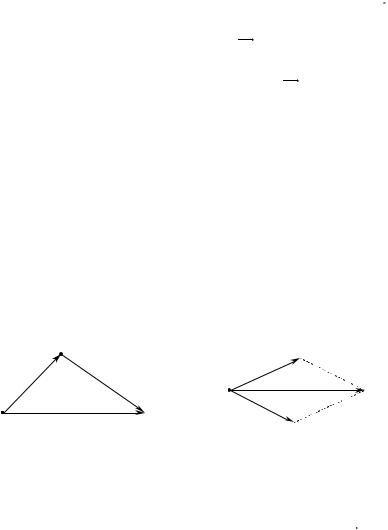
				r					r	то определена
	Если конец вектора a				совпадает с началом вектора b ,					то определена
сумма	r	r	r	называемая суммой по		правилу	треугольника, началом
сумма	c	= a	+ b ,	называемая суммой по		правилу	треугольника, началом
	r				r					r
вектора c		служит начало вектора a , а концом – конец вектора b (рис. 1).
				r					r	то определена
	Если начало вектора a				совпадает с началом вектора b ,					то определена
сумма	r	r	r	называемая суммой по правилу параллелограмма, нача-
сумма	c	= a	+ b ,	называемая суммой по правилу параллелограмма, нача-
лом вектора			r		r	r
лом вектора			c служит начало векторов a и b , а концом – противоположная
вершина параллелограмма, построенного на векторах							r		r
вершина параллелограмма, построенного на векторах							a	и b (рис. 2).
			A					А
						r		А
				r		r
		r		r		a			r
		r		b			r	r	r
		a		b			r	r	+ b
							c	= a	+ b

			r					r
O	r	r	r		B			b
O	c	= a	+ b		B				В
									В
		Рис. 1.							Рис. 2.
Если	начало			r	совпадает				r
Если	начало		вектора a		совпадает			с началом вектораb , то определена
		r	r	r				r	служит конец вычитае-
разность векторов c			= a	- b (рис.3), началом вектора c					служит конец вычитае-
			r							r
мого (конец вектора b ), а концом – конец уменьшаемого (конец вектора										a ).
					r	r	r	называется	r
Суммой трех векторов a						+ b + c		называется	вектор d = OC , замы-

кающий ломаную OABC , построенную из данных векторов (рис. 4).

= a

- b

d = a

+ b + c

Рис. 3.

Рис. 4.

на число (скаляр)

называется новый век-

Произведением вектора a

тор, имеющий длину

(при l > 0 ) или

и направленный одинаково с a

(при l < 0 ).

противоположно a

Задания

96. По сторонам ОА и ОВ прямоугольни-

ка OACB отложены единичные векторы i и

(рис. 5). Выразить через i

j векторы OA ,

NAC , CB , BO , OC и BA , если ОА=3, ОВ=4.

97.Пусть на рис. 5 M – середина ВС и

N –

середина АС. Определить

векторы OM ,

ON и MN , при ОА=3, ОВ=4.

98.

На плоскости даны точки A(0;-2),

B(4;2) и

C(4;-2). В

начале координат прило-

Рис. 5

жены силы OA , OB

и OC . Построить их рав-

нодействующую OM , найти ее величину. Выразить силы OA , OB , OC и

через единичные векторы i и

j координатных осей.

99. Даны три компланарных вектора m ,

p , причем угол между

векторами

равен 300, а

–

600. Построить вектор

и n

между n и

u = m + 2n -

3 p и вычислить его модуль.

Указание: в ломаной, построенной из векторов m

, 2 n и –3

p , продолжить

первое звено до пересечения с третьим.

100. Проверить аналитически и геометрически векторные тождества:

1) a +	b - a	=	a + b	,	2) a -	a + b	=	a - b	.

2		2			2		2

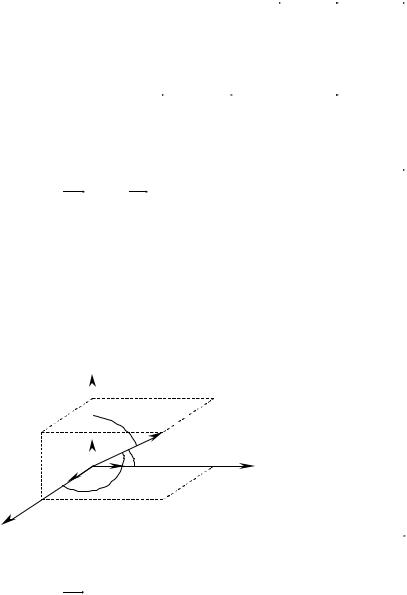
101. На трех некомпланарных векторах OA = a ,

OB = b

и OC = c

построен параллелепипед. Указать те его вектор-диагонали, которые соответ-

r r

ственно равны a

+ b - c , a

- b + c ,

- b - c и b - a - c .

102. С

помощью

чертежа

задачи101

проверить

переместительное

свойство векторной суммы a + b - c

= a

- c

+ b = b + a

- c = b - c

+ a .

103. Даны

– медиана

векторы OA = a

OB = b . Вектор

OC = c

треугольника

OAB . Разложить аналитически и геометрически: 1) вектор

по векторам a

и b ; 2) вектор a

по векторам b и

c .

104. В

прямоугольнике OACB (рис. 5)

M и

– середины

сторон

BC = 3 и AC = 4 . Разложить аналитически и геометрически вектор OC = c

и ON

по векторам OM = a

= b .

Указание: В условие c

= la

+ mb

подставить выражения a ,

и c

через i

и j и сравнить коэффициенты слева и справа при i

j .

105. Даны два перпендикулярных вектора a и b имеющие одно нача-

= 4 , а

= 3 .

ло. Найти длины векторов a

+ b

и a

- b зная, что

§2. Прямоугольные координаты вектора в пространстве.

Направляющие косинусы

Рассмотрим

про-

M 3

странстве

прямоугольную

систему

координат Oxyz .

Выделим на координатных

осях

Ox ,

и Oz

еди-

ничные

векторы

называе-

M 2

мые ортами и обозначае-

M 1

мые

j ,

соответст-

венно. Пусть дана точка

(рис. 6).

Проекция

ее

Р и с . 6 .

радиус-вектора

OM = r

Рис. 6

на

оси

координат

OM1 = x , OM 2 = y и OM 3 = z

называются прямоугольными координата-

или точки M .

ми вектора OM = r

Радиус-вектор выражается через орты:

(1)

r = x i

+ y j + z k ,

а длина (модуль) радиус-вектора определяется по формуле:

	r
	r	= x2 + y 2 + z 2 .			(2)
	r	= x2 + y 2 + z 2 .			(2)
Если вектор задан координатами начала			и	конца, например	точками
A(x1 ; y1 ; z1 ) и B(x2 ; y2 ; z2 ), то проекции вектора			AB на оси координат будут
иметь вид:
прx AB = X = x2 - x1 ,
пр y AB = Y = y2 - y1 ,
прz AB = Z = z2 - z1 .
Таким образом, координатами вектора AB				называются	числа X ,

Y , Z равные разностям соответствующих координат его конца и начала:

AB = (x2 - x1 ; y2 - y1 ; z2 - z1 ).

Следовательно, можно написать формулы аналогичные формулам (1), (2):

AB = X i + Y j + Z k = (x2 - x1 )i +

(y2 - y1 ) j +

(z2 - z1 )k ,

+ y(

)2 + z(

- z )2

= X 2 +Y 2 + Z 2 =

- x

- y

Пусть a , b и g

– углы, образованные вектором AB с осями коорди-

нат. Тогда числа

cosa =

cos b =

, cos g

называются направляющими косинусами вектора AB .

Направляющие косинусы обладают следующим важным свойством:

cos 2 a + cos 2 b + cos 2 g = 1 ,

т.е. сумма квадратов направляющих косинусов вектора равна 1.

Задания

106. Построить точку M (5;-3;4) и определить длину и направление ее

радиус-вектора.

107. Построить вектор

= OM

и определить его длину

= 2i + 3 j + 6 k

направляющие

косинусы(проверить

справедливость

формулы

cos 2 a + cos2 b + cos 2 g = 1 ).

108. Вектор составляет с осямиOx и Oz

углы 400

и 800. Найти

его

угол с осью Oy .

109. Радиус-вектор точки M составляет с осью Ox угол 450 и с осью

Oy угол 600. Его длина			равна6 единицам. Определить координаты	точки
M , если ее координата z			r	через
M , если ее координата z			отрицательна, и выразить вектор OM = r	через
r	r	r
орты i ,	j ,	k .
			r	, его
110. Даны точки A(1;2;3) и B(3;-4;6). Построить вектор AB = u				, его

проекции на оси координат и определить длину и направляющие косинусы

			r	с осями координат.
вектора. Построить углы вектора u				с осями координат.
111.	Построить	параллелограмм			на			r r	и
111.	Построить	параллелограмм			на	векторахOA = i + j			и
r	r
OB = k - 3 j , определить его диагонали.							r
112.	В точке A(2;1;-1) приложена сила величины						r	= 7 . Зная две ко-
112.	В точке A(2;1;-1) приложена сила величины						F	= 7 . Зная две ко-
ординаты этой силы X = 2 и Y = -3 определить направление и конец век-
тора, изображающего силу.			даны точки A(2;4),			B(2;3), C(0;5) и построе-
113.	На плоскости Oxy		даны точки A(2;4),			B(2;3), C(0;5) и построе-
	r	r		r
ны векторы OA = a , OB		= b ,	OC = c . Разложить геометрически и анали-
	r		r	r
тически вектор a по векторам b и				c .				r
114.	Даны точки A(2;2;0) и							r	, его
114.	Даны точки A(2;2;0) и			B(0;-2;5). Построить вектор AB = u					, его

проекции на оси координат и определить длину и направляющие косинусы

вектора. Построить углы вектора u с осями координат.

115. Вектор OM = r составляет с осями координат равные острые уг-

лы. Определить эти углы и построить вектор r , если его длина равна 2 3 . 116. Вектор составляет с осями Oy и Oz углы 600 и 1200. Какой угол

он составляет с осью Ox ?

117. Даны три последовательные вершины параллелограмма A(1;-2;3),

B(3;2;1)	и C(6;4;4). Найти его четвертую вершину D .						r
118.		На	плоскости Oxy		построить	r
						векторыOA = a	= 2i ,
r	r	r	r	r	r
OB = b = 3 i + 3 j ,			OC = c = 2i + 6 j . Разложить геометрически и аналити-
чески вектор		r	r	r
		c по векторам a		и b .

§3. Скалярное произведение векторов

Скалярным произведением двух векторовназывается произведение их длин, умноженное на косинус угла между ними.

Скалярное произведение век-

тора

обозначается

a на вектор

r r

× b

или (a, b ) и определяется ра-

венством:

cos j .

× b =

Из

рис.

видно,

что

cos j = прarb . Поэтому

× b

cos j =

прrb =

пр r a

b cos j

Рис.. 7.

Скалярное произведение век-

торов

обладает

следующими

свой-

ствами:

× b = b × a – переместительный закон.

– распределительный закон.

(b +

c )=

× b +

× c

Если векторы

и b параллельны, то a

× b = ±

Если векторы

cos 900

= 0 .

и b перпендикулярны, то a

× b =

Скалярное произведение ортов:

r r

i × j = 0 , i × k = 0 ,

j × k = 0 , i × i = 1 ,

j × j = 1 , k × k = 1 .

Если

векторы

заданы

координатами:

(x1; y1; z1 )

a =

b = (x2 ; y2 ; z2 ), то

a × b = x1 x2 + y1 y2 + z1 z2 .

Из

свойств

скалярного произведения

векторов

следует, что

косинус

= (x1; y1; z1 )

угла образованного ненулевыми векторамиa

и b = (x2 ; y2 ; z2 )

равен:

x1 x2 + y1 y2 + z1 z2

cos j =

× b

+ y2 + z 2

x2 + y2 + z 2

име-

Таким образом, условие параллельности двух векторов b = m a

ет вид:

= m , а условие перпендикулярности – a

× b = 0

или

x1 x2 + y1 y2 + z1 z2 = 0 .

Кроме того,

скалярное произведение позволяет записать условие того,

что вектор имеет единичную длину в виде a

× a = 1 .

Пример 1. В банке, в течение дня был произведен обмен трех валют в объеме 1000, 230, 2156 у.е. на рубли по курсу 36, 18, 0.5 руб. за 1 у.е. Необходимо определить объем V операций банка по обмену валют за день в рубле-

вом эквиваленте.	r	= (1000; 230; 2156), а
Решение: Вектор
	объема валют имеет видa
вектор курсов обмена –	r
	b = (36;18; 0.5). Следовательно, объем V операций

банка по обмену валют за день можно определить как скалярное произведе-

r r

ние векторов a и b . Таким образом,

r r

V = a × b = 1000 × 36 + 230 × 18 + 2156 × 0.5 = 41218 руб.

Пример 2. Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в таблице:

Вид изделия,	Количество	Расход	Норма времени	Цена изде-
Вид изделия,	Количество	сырья,	изготовления,	лия,
№ п/п	изделий, ед.	сырья,	изготовления,	лия,
№ п/п	изделий, ед.	кг.	ч/изд.	ден.ед/изд.
		кг.	ч/изд.	ден.ед/изд.
1	20	5	10	30
2	50	2	5	15
3	30	7	15	45
4	40	4	8	20

Требуется определить следующие ежесуточные показатели: расход сырья S , затраты рабочего времени T и стоимость выпускаемой предприятием продукции P .

Решение: По данным таблицы составим четыре вектора, характеризующие весь производственный цикл:

r	= (20; 50; 30;	40) – вектор ассортимента,
q
r	= (5; 2; 7; 4) – вектор расхода сырья,
s
r	= (10; 5;15; 8)	– вектор затрат рабочего времени,
t
r	= (30;15; 45;	20) – ценовой вектор.
p

Тогда искомые величины будут представлять собой соответствую-

щие скалярные произведения вектора					r	на три других век-
					ассортиментаq
тора, т.е.		r
S	r		= 20	× 5 + 50 × 2 + 30 × 7	+ 40 × 4 = 570 кг,
	= q	× s
T	r	r	= 20	×10 + 50 × 5 + 30 ×15 + 40 × 8 = 1220		ч,
	= q	× t
	r	r		× 30 + 50 ×15 + 30	× 45 + 40 × 20 = 3500 ден. ед.
P = q		× p = 20

Пример 3. В некотором безденежном хозяйстве сложилось устойчивое равновесие при ежедневном производстве100 кг муки, 50 л молока, 40 м ткани, 20 пар обуви и следующих пропорциях обмена: 1л молока=3 кг муки; 1м ткани=5 кг муки; 1 пара обуви = 8 кг муки. Найти величину номинального национального дохода.

Решение: Вектор, отражающий объемы ежедневного производства

имеет вид	r	= (100; 50; 40; 20). Приняв 1 кг муки в качестве масштаба цен,
имеет вид	q
			r	= (1; 3; 5; 8). Тогда, вели-
получим вектор равновесных относительных цен p				= (1; 3; 5; 8). Тогда, вели-
чина реального национального дохода составит:
		r	r	× 8 = 610 ,
		P = q	× p = 100 ×1 + 50 × 3 + 40 × 5 + 20	× 8 = 610 ,

т.е. ценность всего набора производимых благ эквивалента ценности610 кг муки.

Допустим, что в данном хозяйстве решили перейти на денежное измерение благ и денежная цена 1 кг муки установилась равной 6 ден. ед. Тогда

r = ( )

образуется следующий вектор денежных цен p 6;18; 30; 48 . В этом случае величина номинального национального дохода составит:

r r

P = q × p = 100 × 6 + 50 × 18 + 40 × 30 + 20 × 48 = 3660 ден. ед.

Если по каким-то причинам денежная оценка муки удвоится, то произойдет удвоение уровня цен, что найдет соответствующее отражение в индексе Ласпейреса.

Задания.

		119.	Определить	угол	между		r	r	r	и
		119.	Определить	угол	между		векторамиa = -i		+ j	и
r	r	r	r
b	= i	- 2 j + 2 k .				вершинамиA(2;-1;3),		B(1;1;1)
		120.	Определить	углы DABC	с	вершинамиA(2;-1;3),		B(1;1;1)		и
C(0;0;5).			Даны точки A(a;0;0), B(0;0;2a)			и C(a;0; a). Построить
		121.	Даны точки A(a;0;0), B(0;0;2a)			и C(a;0; a). Построить			векторы
OC ,		AB и найти угол между ними.

122. На плоскости дан треугольник с вершинамиO(0;0), A(2a;0) и

B(a;-a). Найти угол, образованный стороной OB и медианой OM этого треугольника.

123.Найти угол между биссектрисами углов xOy и yOz .

124.Из вершины квадрата проведены прямые, делящие противоположные стороны пополам. Найти угол между этими прямыми.

125.Найти угол между диагоналями параллелограмма, построенного

на векторах a

= 2 i

+ j

и b

= -2 j + k .

126.

Даны

векторы a

= i

+ j + 2 k

= i

- j + 4 k . Определить

прbr a

и прarb .

127. Раскрыть скобки в выражении

r 2

(2 i - j )

× j +

(j - 2 k )× k + (i - 2 k ) .

128. Вычислить: 1)

– единичные векторы с уг-

+ n)2 , если

r 2

лом между ними 30°; 2)

= 2

2 ,

= 4 и угол между ними

- b ) , если

равен 135°.

129. Раскрыть скобки в выражениях:

r 2

1) (a

+ b ) ;

2) (a + b ) +

- b )

и выяснить геометрический смысл полученных формул.

= 3 ,

= 2 ,

130. Даны компланарные векторы a , b

c , причем

æ r

Ù rö

æ rÙ rö

r r

= 60

. Построить вектор u = a + b - c

и вы-

5 , ça

, b ÷

çb, c

числить его модуль по формуле

r 2

(a + b - c ) .

131. Найти величину равнодействующих четырех компланарных сил, приложенных к точке O , если величина каждой силы равна 10, а угол между

двумя последовательными силами равен 45°.
	132. Определить длины диагоналей параллелограмма, построенного на
	r	r	r	r	r	r	r	и	r	– единичные векторы, угол
векторах a		= 2 m	+ n и b = m			- 2 n , где	m	и	n	– единичные векторы, угол
меду которыми 60°.					r	r	r		r
			r		r	r	r	и	r	– единичные векторы, угол
	133. Дан вектор a			= 2 m - n , где			m	и	n	– единичные векторы, угол
										r	r
меду которыми 120°. Найти косинусы углов образованных векторами a											и m ;
r	r
a	и n .

134. Определить угол между биссектрисами двух плоских углов правильного тетраэдра, проведенными из одной его вершины.

Указание. Если m ,

n и

p – единичные векторы ребер, то m + n и

m + p –

векторы, направленные по биссектрисам.

135. На осях Ox ,

Oy и Oz

отложить равные отрезки a = 4

и на них

построить куб. Пусть M – центр верхней грани, а N – центр правой боковой

грани куба. Определить векторы OM и

ON и угол между ними.

136.

Даны

векторы

причем

= 2 ,

= 4 , а

OA = a

OB = b ,

Определить угол между

медианойOM

треугольника AOB и

(a, b) = 60o .

стороной OA .

137. Из вершины прямоугольника со сторонами 6 см и 4 см проведены

прямые, делящие противоположные стороны пополам. Найти угол j

между

ними.

138. Даны три последовательные вершины

параллелограмма:

A(- 3; - 2; 0),

В(3; –3;

1) и

C = (5; 0; 2). Найти его четвертую

вершинуD и

угол между векторами

139.

Даны

точки A(3; 3;

–2),

B(0;

–3; 4),

C = (0; - 3; 0)

и D(0; 2; –4). Построить

векторы

AB = a

и CD = b и найти пр a b .

140. В равнобедренной трапецииОАСВ (рис. 8), М и N — середины

сторон ВС = 2 и AС = 2. Острый угол трапеции 60°. Определить угол между

векторами OM и ON .

141. Найти угол между векторами a =

+ 4n

и b = m

- n , где m и

– единичные векторы, образующие угол 120°.

142. Показать, что угол между диагоналями прямоугольника, постро-

енного

на

определяется

формулой

векторахa

( a ^ b ),

cos j = ±

- b2

a 2

+ b2

143.

Проекции

перемещения

движущейся

точки

на

оси

координат

S x

= 2 м, S y

= 1 м, S z

= – 2 м. Проекции действующей силы F на оси коор-

динат равны Fx

= 5 Н,

= 4 Н и

Fz = 3 Н. Вычислить работу

силы

F ( A = F × s)

и угол между силой F и перемещением s .

144. К вершине правильного тетраэдра с ребром а приложены три силы, изображаемые его вектор-ребрами. Определить величину равнодействующей.

r r	+	r	r	r	r
Указание. Искомая величина равна a (m + n	+	p)3 где	m ,	n и	p – единич-

ные векторы данных сил.

145. Квадрат разделен на три полосы одинаковой ширины и затем свернут в правильную треугольную призму. Найти угол между двумя смежными звеньями ломаной, образованной при этом диагональю квадрата.

§4. Векторное произведение векторов.
	Векторным			произведением	вектора
	Векторным			произведением	вектора
	r		r
	a на вектор b называется такой третий век-
	r
	тор c (рис. 9), который:
1)		имеет		модуль, численно	равный
	площади	параллелограмма, построенного на
	векторах	r	r
	векторах	a	и b ;

2)перпендикулярен к плоскости параллелограмма;

3)направлен в такую сторону, с кото-

r r

рой кратчайшее вращение от a к b рассматривается совершающимся против часовой стрелки. Такое расположение век-

торов a

b и

c называется правой тройкой векторов (правой связкой).

или

r r

]. Таким обра-

зом,

Векторное произведение обозначается a

´ b

[a, b

если:

´ b = c ,

sin j ,

´ b |=

^ a

и c

^ b ,

, b ,

c составляют правую тройку векторов.

Векторное произведение обладает следующими свойствами:

´ b = -b ´ a ,

2. l (a ´ b )=

(l a)´ b = a ´

(l b ),

– распределительный закон.

´ (b + c)

= a ´ b + a

´ c

4. Если

a || b , то a

´ b = 0 ; в частности,

´ a = 0 .

5. Векторные произведения ортов определяются равенствами:

i ´ j = k ,

j ´ k = i ,

k ´ i = j .

Вообще произведение любых двух смежных векторов в последовательности

¾¾¾® +

ijkij

- ¬¾¾¾

дает следующий вектор со знаком «+», а в обратной последовательности – со знаком «-»,

Выражение векторного произведения через координаты сомножителей

r	, y1 , z1 )	r
a(x1	, y1 , z1 )	и b (x2 , y2 , z2 ) имеет вид:				r
				r	r	r
		r	r	i	j	k
		r	r	x1	y1	z1	.
		a	´ b =	x1	y1	z1	.
				x2	y2	z2

Из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах определяется по формуле

r	r
S o =\| a	´ b \| ,

а площадь треугольника, построенного на векторах a

		1	r	r
SD	=		\| a	´ b \| .

	2

Задания.

и b :

146. Определить и построить вектор с

= a

´ b , если:

r r

= 3 i , b = 2 k ; 2)

= i + j , b = i - j ; 3)

= 2 i + 3 j ,

= 3 j + 2 k .

Найти в каждом

случае

площадь

параллелограмма, построенного

на

векторах

и b .

147.Вычислить площадь треугольника с вершинамиA(7;3;4), В(1;0;6)

иС(4;5; –2).

148. Построить	параллелограмм	на	векторах	r	r r
				a	=и 2 j + k и

r r r

b= i + 2 k и вычислить его площадь и высоту.

149.Раскрыть скобки и упростить выражения: 1) i ´ ( j + k) - j ´ (i + k) + k ´ (i + j + k) ;

2)(a + b + c) ´ c + (a + b + c) ´ b + b + (b - c) ´ a ;

3)(2a + b) ´ (c - a) + (b + c) ´ (a + b) ;

4)2i( j ´ k) + 3 j(i ´ k) + 4k(i ´ j) .

150. Доказать, что

и выяснить

геометри-

(a - b ) ´ (a

+ b ) =

2 a

´ b ,

ческое значение этого тождества.

151. Векторы

a и

b составляют угол 45°. Найти площадь треуголь-

ника, построенного на векторах a - 2 b и

3 a

+ 2 b , если | a |=| b |= 5 .

152. Найти площадь параллелограмма, диагоналями которого служат

r r

— единичные векторы, образую-

векторы 2 m - n и

4 m

- 5 n , где

щие угол 45°.

Указание. Имеем a

+ b =

- n

- b =

4 m

- 5 n , где

m и

n — век-

торы-стороны параллелограмма.

Перемножив, найдем вектор 2 b ´ a , модуль ко-

торого и равен удвоенной искомой площади.

153. Построить векторы

a = 3 k

- 2 j ,

b = 3 i

- 2 j

и c

= a

´ b . Вы-

числить модуль вектора c и площадь треугольника, построенного на векто-

рах a и b .

154.Построить треугольник с вершинами A(1;-2;8), B(0;0;4) и С(6;2;0). Вычислить его площадь и высоту BD.

155.Вычислить диагонали и площадь параллелограмма, построенного

на векторах

a = k - j и b

= i

+ j + k .

156. Доказать, что (2 a + b) ´

(a + 2 b ) = 3 a

´ b .

157.

Найти

площадь

параллелограмма, построенного на векторах

– единичные векторы, образующие

= m +

2 n и b =

2 m

+ n

, где m

и n

угол 30°.

§5. Смешанное произведение векторов.

Смешанным произведением векторов a , b и

c называется выраже-

ние вида

´ b) × c .

Выражение

смешанного

произведения

через

координаты сомножите-

, y3 , z3 ) имеет вид:

лей a(x1 , y1 , z1 ) ,

b (x2 , y2 , z2 ) и c(x3

´ b )× c

т.е. смешанное произведение векторов равно определителю третьего порядка, строками которого являются соответствующие координаты этих векторов.

Смешанное произведение обладает следующими свойствами:

1. Смешанное произведение не меняется при циклической перестановке его сомножителей:

´ b ) × c

= (b ´ c)

× a

= (c ´ a)

× b .

2. От перестановки двух любых сомножителей смешанное произведе-

ние меняет знак:

(a ´ b ) × c = -(a ´ c )

× b = -(c

´ b ) × a .

3. Если два из трех данных векторов равны или параллельны, то их

смешанное произведение равно 0.

Знаки

операции «точка»

«крест»

можно

поменять

местами:

что позволяет записывать смешанное произведение в

´ b) × c

a × (b ´ c)

r r

, т. е. без знаков действий и без скобок.

виде a b c

Смешанное произведение векторов имеет следующие приложения:

1. Определение взаимной ориентации векторов a

, b и

c в простран-

стве. Если

r r

> 0 , то

– правая тройка векторов, а если

r r r

< 0

a b c

a ,

b ,

a b c

– левая тройка векторов.

Установление компланарности векторов. Если

компла-

и c

нарны, то

r r

= 0 , и обратно. При этом,

существует ли-

a b c

между a , b

нейная зависимость вида c

= m a

+ n b .

Нахождение

объемов

параллелепипеда

треугольной

пирамиды

(тетраэдра). Объем параллелепипеда, построенного на

векторах a

и c

вычисляется по формуле:

r r

V =

a b c

а объем тетраэдра, построенного на этих же векторах, равен

r r

a b c

Задания.

158.

Построить

параллелепипед

на

векторахa = 3 i

+ 4 j ,

и вычислить его объем. Правой или левой будет

= -3 j + k , c

= 2 j + 5 k

связка векторов

r r

(a, b , c)

159.Построить пирамиду с вершинами О(0; 0; 0) А(5; 2; 0), B(2; 5; 0) и С(1; 2; 4) и вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.

160.Показать, что точки А (2; –1; –2), B(l; 2; 1), С(2; 3; 0) и D(5; 0; –6)

лежат в одной плоскости.

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.12.2018159.74 Кб2Лекция трудовые отношения.doc
#
05.06.2015107.87 Кб14Лекция №34.pdf
#
05.06.20151.42 Mб4лекция19ноября2014.pdf
#
05.06.2015688.32 Кб5Лекция1_prezent.pdf
#
05.06.20151.15 Mб7Лекция2_презент.pdf
#
05.06.2015916.62 Кб42Лесев.pdf
#
26.09.2019129.31 Кб8Линал 1-21.docx
#
05.06.2015295.09 Кб17линал бдз.pdf
#
23.09.20192.72 Mб11Линал готовый.docx
#
05.06.2015426.81 Кб29Линейная алгебра.pdf
#
04.06.201517.76 Кб57Литература (АВТ).docx

одной какой-нибудь буквой, например,

Длина или модуль вектора обозначается через