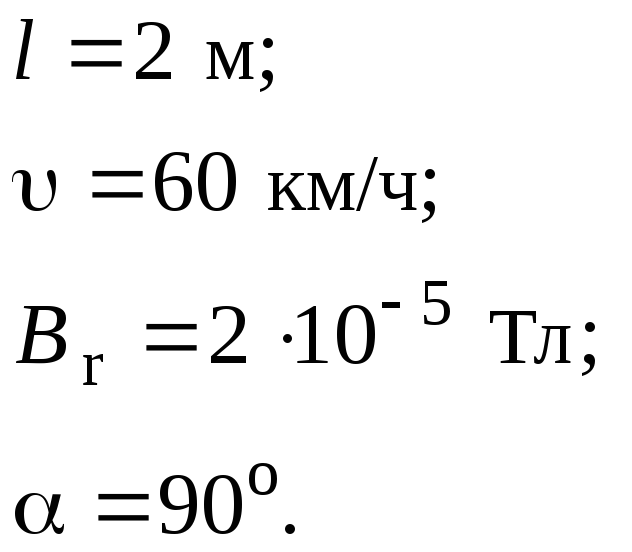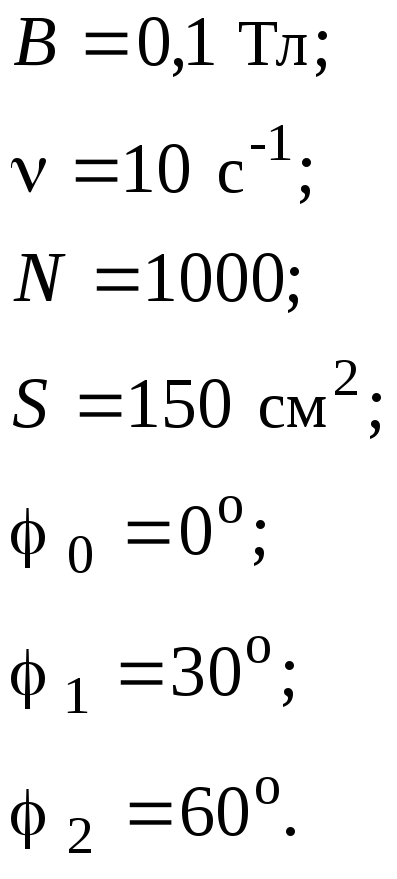Задача 3.8

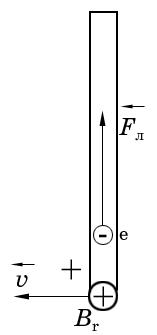
Автомобильная антенна (вертикальный проводник) длиной 2 м движется с востока на запад в магнитном поле Земли со скоростью 60 км/ч. Вычислить разность потенциалов между концами проводника. Горизонтальную составляющую индукции магнитного поля Земли принять равной 210^-5 Тл.

Дано:	Рис. 3.8
U = ?

Решение

Так как проводник разомкнут, тока в нем не будет, и разность потенциалов U на концах проводника равна ЭДС индукции:

U = B l υ sin ,

где l – длина проводника;

υ – скорость его движения;

 – угол между векторами .

Смещение электронов в вертикальной антенне автомобиля под действием силы Лоренца происходит за счет горизонтальной составляющей индукции магнитного поля Земли, т.е. . Так как силовые линии магнитного поля Земли направлены с юга на север, то под действием электроны переместятся к верхнему концу антенны. Таким образом, нижний конец антенны зарядит- ся положительно и будет иметь более высокий потенциал, чем верхний.

Возникшая разность потенциалов равна

.

Произведем вычисления:

.

Задача 3.9

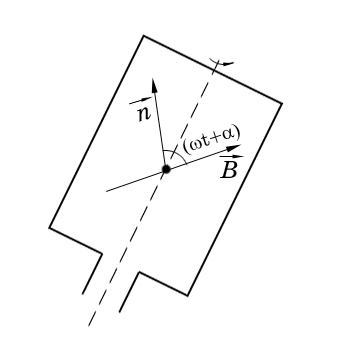
В однородном магнитном поле (В = 0,1 Тл) равномерно с частотой 10 с^-1 вращается рамка, содержащая 1000 витков, плотно прилегающих друг к другу. Площадь рамки – 150 cм². Ее вращение совершается вокруг оси, лежащей в ее плоскости и перпендикулярной линиям магнитной индукции. Найти максимальную ЭДС индукции во вращающейся рамке. Определить количество электричества, которое протечет через рамку за время ее поворота на угол 30 в случаях, если угол поворота рамки изменяется: 1) от 0 до 30; 2) от 30 до 60. Сопротивление рамки принять равным 10 Ом (рис. 3.9).

Дано:	Рис. 3.9

Решение

ЭДС электромагнитной индукции определяется уравнением

(3.35)

где  – потокосцепление, равное в данном случае  = ФN.

При вращении рамки магнитный поток, пронизывающий рамку в момент времени t, определяется уравнением

Ф = B S cos (t + ), (3.36)

где α – угол, образуемый нормалью к поверхноcти рамки и направ-лением силовых линий при t = 0;

–циклическая (круговая) частота.

С учетом (3.36) выражение для ЭДС индукции принимает вид

. (3.37)

Из выражения (3.37) вытекает

. (3.38)

Произведем вычисления:

.

Мгновенное значение индуктивного тока в рамке определяется законом Ома

,

где R – сопротивление.

. (3.39)

Мгновенное значение тока

,

поэтому (3.39) можно переписать в виде

(3.40)

После интегрирования выражения (3.40) получим

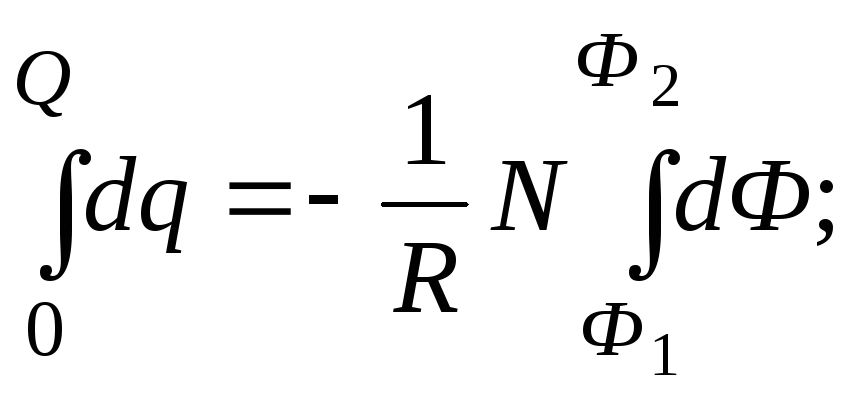
(3.41)

.

Так как , окончательно имеем

. (3.42)

В первом случае

.

Во втором случае

.

Произведем вычисления:

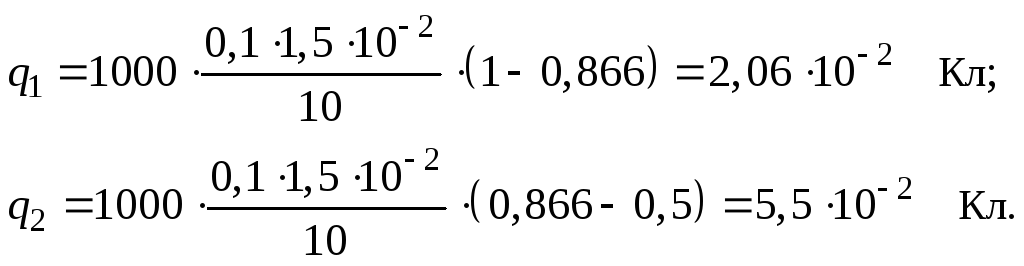
Задача 3.10

При некоторой величине тока плотность энергии магнитного поля длинного соленоида без сердечника равна 0,2 Дж/м³. Во сколько раз увеличится плотность энергии поля при том же токе, если соленоид будет иметь сердечник? При решении задачи воспользоваться графиком рис. 3.10.

Дано:	Рис. 3.10
= ?