Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет технологий управления и гуманитаризации

Кафедра «Таможенное дело»

Методические указания и задания

к лабораторным работам

по курсу

«Компьютерные и информационные технологии»

Раздел "Технологии использования

прикладных программ

для решения экономических задач"

для студентов экономических специальностей

Минск 2012

УДК 681.3 (075.8)

В настоящем издании даны методические рекомендации и задания к лабораторным работам по курсу "Компьютерные и информационные технологии". Целью данных работ является изучение возможностей и получение навыков, необходимых для решения экономических задач средствами MSExcel. Подробно рассматривается регрессионный анализ, работа с надстройкой "Поиск решения" и использование некоторых финансовых функций.

Составители:

Т.А.Галай,

Рецензенты:

Содержание

Лабораторная работа №1. Использование регрессионного анализа в решении экономических задач. 4

1.1. Цель работы. 4

1.2. Методические рекомендации. 4

1.3. Задания. 11

Лабораторная работа №2. Использование надстройки "Поиск решения". 14

2.1. Цель работы. 14

2.2. Методические рекомендации. 14

2.3. Задание. 18

Лабораторная работа №3. Решение экономических задач с использованием финансовых функций Excel. 21

3.1. Цель работы. 21

3.2. Методические рекомендации. 21

3.3. Задание. 25

Содержание отчета: 28

1. Использование регрессионного анализа в решении экономических задач.

   1. Цель работы.

Научиться использовать функции, аппроксимирующие известные данные по линейной и экспоненциальной зависимости. Исследовать множественную линейную регрессию.

2. Методические рекомендации.

   1. Функции регрессии.

Для решения различных экономических задач широко используются электронные таблицы Excel. Например, для обработки статистической информации вExcelпредусмотрены функции регрессии, которые вычисляют параметры для линий, наилучшим образом аппроксимирующих функциональные зависимости.

Регрессия– это широко применяемый в статистике способ формирования уравнения, которое наилучшим образом описывает последовательность данных.

Попросту говоря, если мы имеем некоторую последовательность данных (см. Рис. 1), мы можем попытаться подобрать функцию, наилучшим образом описывающую полученную зависимость (см. Рис.2 и Рис.3).

Рисунок 1. Известные данные.

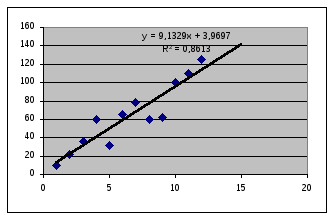
Рисунок 2. Аппроксимация по прямой.

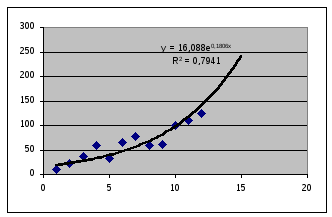
Рисунок 3. Аппроксимация по экспоненте.

Далее мы должны оценить, какая линия описывает нашу зависимость наиболее точно, используя величину достоверности (R²) или коэффициент корреляции (функция КОРРЕЛ). В нашем примере наиболее достоверна аппроксимация по прямой. Следовательно, именно эта функция даст наиболее достоверное предсказание для будущих значений.

В следующей таблице приведены функции регрессии Excel.

Таблица 1. Описание основных функций регрессионного анализа.

Синтаксис	Описание
ЛИНЕЙН (известные_значения_y; известные_значе­ния_x; константа; статистика)	Возвращает массив, описывающий прямую, наилучшим способом аппроксимирующую имеющиеся данные (в соответствии с методом наименьших квадратов).
ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x; новые_значения_x; константа)	Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой (по методу наименьших квадратов) массивы известные_значения_yиизвестные_значения_x. Возвращает значенияy, в соответствии с этой прямой для заданного массивановые_значения_x.
ПРЕДСКАЗ (новое_значение_x; известные_значения_y; известные_значения_x)	Вычисляет будущее значение yпо существующим значениямxна основе линейной регрессии для массивовизвестные_ значения_ y;известные_ значения_ x.
НАКЛОН (известные_значения_y; известные_значения_x)	Возвращает наклон линии линейной регрессии, заданной точками известные_значения_yиизвестные_значения_x (построенной по методу наименьших квадратов).
СТОШYX (известные_значения_y; известные_значения_x)	Возвращает стандартную ошибку предска­занных значений yдля каждого значенияxв регрессии. Стандартная ошибка - это мера ошибки предсказанного значенияyдля отдельного значенияx.
ЛГРФПРИБЛ (известные_значения_y; известные_значения_x; константа; статистика)	В регрессивном анализе вычисляет экспоненциальную кривую, аппроксимирующую данные и возвращает массив значений, описывающий эту кривую.
РОСТ (известные_значения_y; известные_значения_x; новые_значения_x; константа)	Аппроксимирует экспоненциальную кривую (известные_значения_y;известные_значения_x) и возвращает соответствующие этой кривой значения y, определяемые аргументомновые_значения_x. Функция РОСТ может применяться также для аппроксимации существу­ющихx-иy-значений экспоненциальной кривой
КОРРЕЛ (известные_значения_y; новые_значения_ y)	Возвращает коэффициент корреляции, показывающий насколько достоверны полученные данные. Коэффициент корреляции имеет значение от 0 до 1. Чем ближе к 1, тем достовернее результат.

Обратите внимание, что функции ЛИНЕЙН и ТЕНДЕНЦИЯ фактически возвращают одну и ту же прямую. Отличие заключается в том, что функция ЛИНЕЙН возвращает уравнение прямой y = mx + b (коэффициентыmиb), а ТЕНДЕНЦИЯ вычисляет значенияyдля всех известныхx. Функция ПРЕДСКАЗ возвращает единственное значениеyдля новогоx.

Функции ЛГРФПРИБЛ и РОСТ аналогичны ЛИНЕЙН и ТЕНДЕНЦИЯ, но описывают не прямую, а экспоненту (y = b m^x).

Некоторые из этих функций (ЛИНЕЙН и ЛГРФПРИБЛ) возвращают массивы значений, поэтому они должны вводиться как формулы для работы с массивами.

Напоминаем, что формула массиваможет выполнить несколько вычислений, а затем вернуть одно значение или группу значений. Формула массива создается так же, как и простая формула. Выделяется ячейка или группа ячеек, в которых необходимо создать формулу, вводится формула, а затем нажимаются клавиши CTRL+SHIFT+ENTER.