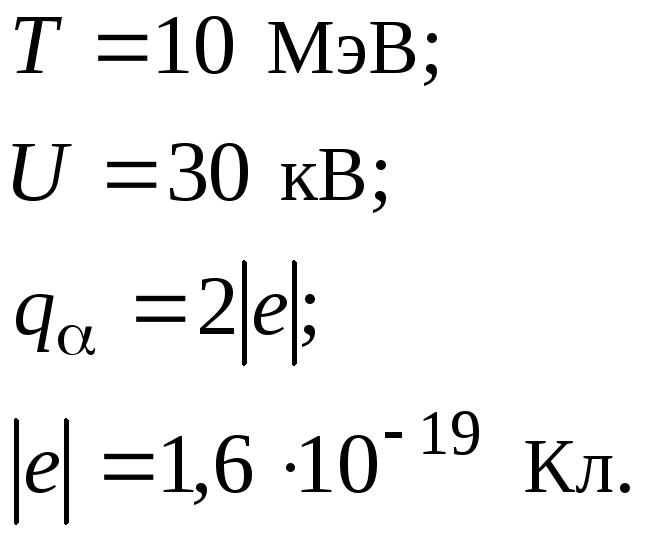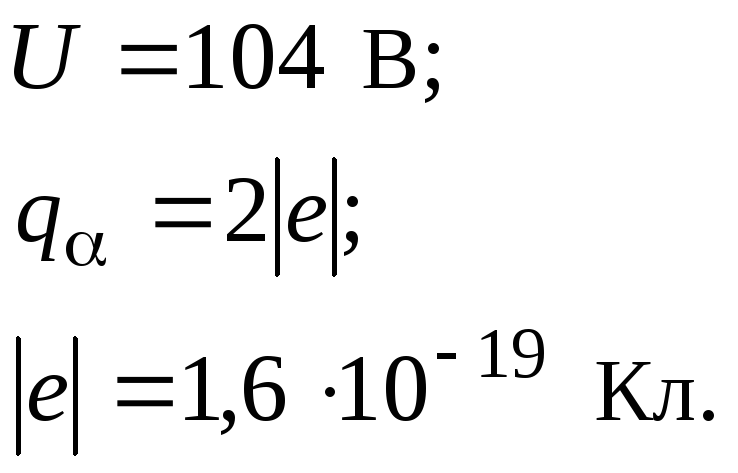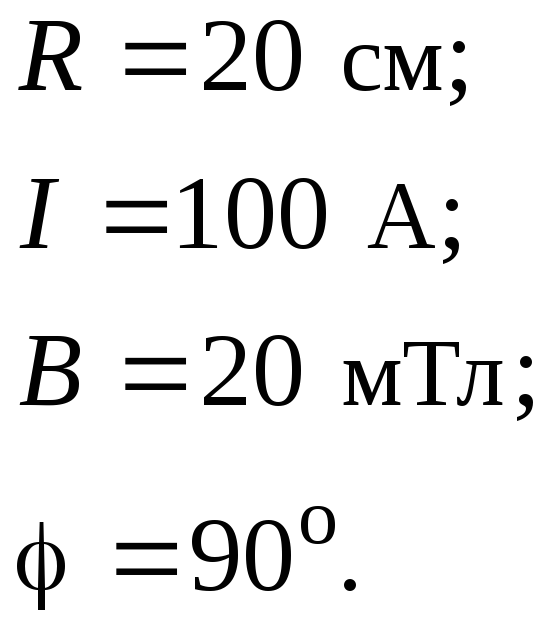Задача 3.5

Определить число оборотов, которые должна сделать -частица, чтобы в магнитном поле циклотрона приобрести кинетическую энергию 10 МэВ, если при каждом обороте она проходит между дуантами. Разность потенциалов – 30 кВ.

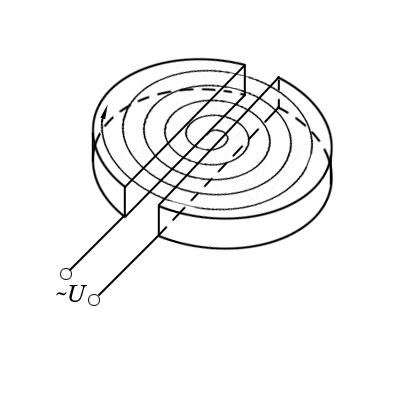
Дано:	Рис. 3.5
N = ?

Решение

Циклотрон состоит из двух электродов в виде половинок металлической круглой коробки, называемых дуантами, на которые подается переменное напряжение U. Дуанты помещены в однородное магнитное поле, перпендикулярное их плоскости. Заряженная частица, попавшая внутрь дуантов, будет двигаться по окружности радиусом , причем период ее обращения не зависит от скорости частицы.

Описав полуокружность за время t = T/2, заряженная частица влетает в электрическое поле в тот момент, когда разность потенциалов достигает максимального значения U_max, ускоряется им и приобретает энергию W = qU_max. При совпадении периода обращения заряженной частицы и периода изменения разности потенциалов частица дважды в течение одного периода пролетает между дуантами. Совершив N оборотов, -частица пролетит между дуантами 2N раз и, следовательно, приобретет энергию

.

Следовательно, число оборотов равно

.

Произведем вычисления:

Задача 3.6

Альфа-частица прошла ускоряющую разность потенциалов 104 В и влетела в скрещенные под прямым углом электрическое и магнитное поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, она не испытывает отклонений от прямолинейной траектории.

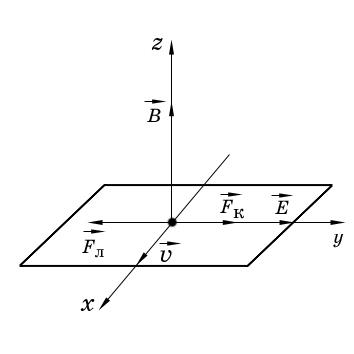
Дано:	Рис. 3.6

Решение

Для того, чтобы найти отношение заряда q к массе альфа-час-тицы m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частицы:

,

откуда

. (3.29)

Скорость υ альфа-частицы найдем из следующих соображений. В рассматриваемом случае на движущуюся заряженную частицу действуют две силы:

1) сила Лоренца , направленная перпендикулярно скоростии вектору магнитной индукции;

2) кулоновская сила , сонаправленная с вектором напряженностиэлектростатического поля ().

Направления всех величин показаны на рис. 3.6. Альфа-частица не будет испытывать отклонения, если геометрическая сумма будет равна нулю:

.

В проекции на ось ОY получим следующее выражение:

,

откуда

.

Подставив это выражение в формулу (3.29), получим

.

Произведем вычисления:

Задача 3.7

По тонкому проводу в виде кольца радиусом 20 см течет ток 100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с магнитной индукцией 20 мТл. Определить работу внешних сил, которую надо совершить, чтобы повернуть кольцо на угол 90 вокруг оси, совпадающей с одним из диаметров кольца.

Дано:	Рис. 3.7
A = ?

Решение

На контур с током в виде кольца в магнитном поле с индукцией B действует момент силы

, (3.30)

где – магнитный момент;

–угол между .

В начальном положении угол , следовательно,М = 0. Отличный от нуля момент силы возникает в том случае, когда внешние силы выведут контур из положения равновесия. Против этого момента и будет совершаться работа внешних сил

. (3.31)

Работа при повороте на конечный угол  равна

. (3.32)

В рассматриваемом случае работа внешних сил определяется выражением

. (3.33)

Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна

, (3.34)

где – магнитный поток, пронизывающий контур в начальный момент времени;

–магнитный поток, пронизывающий контур после поворота.

Следовательно,

A = Ir²B,

что совпадает с формулой (3.33).

Произведем вычисления:

A = 100  3,14  0,2²  0,02 = 0,251 Дж.