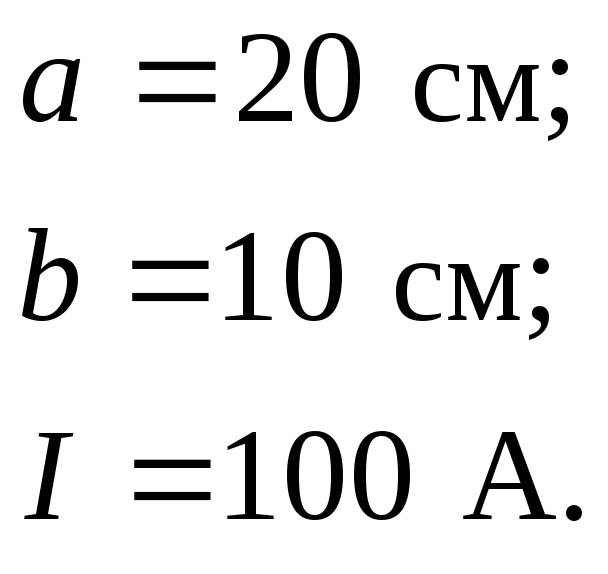- •Рабочая программа по курсУ физики
- •2. Элементы специальной (частной) теории относительности
- •3. Механические колебания и волны в упругих средах
- •4. Основы молекулярной физики и термодинамики
- •5. Электростатика
- •6. Постоянный электрический ток
- •7. Электромагнетизм
- •8. Электромагнитные колебания и волны
- •9. Волновая оптика
- •10. Квантовая природа излучения
- •11. Элементы атомной физики и квантовой механики
- •12. Элементы квантовой статистики и физики твердого тела
- •13. Элементы физики атомного ядра и элементарных частиц
- •Методические указания к рабочей программе
- •Методические указания к выполнению контрольных работ
- •1. Физические основы классической механики.
- •Задача 1.3
- •Решение
- •Задача 1.4
- •Решение
- •Задача 1.5
- •Решение
- •Задача 1.6
- •Решение
- •Задача 1.7
- •Решение
- •Задача 1.8
- •Решение
- •Задача 1.9
- •Решение
- •Задача 1.10
- •Решение
- •Задача 1.11
- •Решение
- •Задача 1.12
- •Решение
- •Задача 1.13
- •Решение
- •Задача 1.14
- •Решение
- •Задача 1.15
- •Решение
- •Задача 1.16
- •Решение
- •Задача 1.17
- •Решение
- •Задача 1.18
- •Решение
- •Задача 1.19
- •Решение
- •Контрольная работа №1
- •2. Электростатика.
- •Задача 2.2
- •Решение
- •Задача 2.3
- •Решение
- •Задача 2.4
- •Решение
- •Задача 2.5
- •Решение
- •Задача 2.6
- •Решение
- •Задача 2.7
- •Решение
- •Задача 2.8
- •Решение
- •Задача 2.9
- •Решение
- •Задача 2.10
- •Решение
- •Задача 2.11
- •Решение
- •Контрольная работа №2
- •3. Электромагнетизм Примеры решения задач Задача 3.1
- •Решение
- •Задача 3.2
- •Решение
- •Задача 3.3
- •Решение
- •Задача 3.4
- •Решение
- •Задача 3.5
- •Решение
- •Задача 3.6
- •Решение
- •Задача 3.7
- •Решение
- •Задача 3.8
- •Решение
- •Задача 3.9
- •Решение
- •Задача 3.10
- •Решение
- •Задача 3.11
- •Решение
- •Контрольная работа №3
- •4. Оптика. Элементы атомной физики
- •Волновые свойства частиц
- •Боровская теория водородоподобного атома
- •Атомное ядро. Радиоактивность
- •Теплоемкость кристалла
- •Элементы квантовой статистики
- •Дозы радиационного облучения
- •Полупроводники
- •Контрольная работа №4
- •Литература Основная
- •Дополнительная
- •Содержание
- •220013, Минск, проспект ф.Скорины, 65.
3. Электромагнетизм Примеры решения задач Задача 3.1
По проводнику, изогнутому в виде прямоугольника со сторонами 20 и 10 см, течет ток силой 100 А. Найти магнитную индукцию в точке пересечения диагоналей прямоугольника.
|
Дано:
|
Рис. 3.1 |
|
B = ? |
Решение
Расположим виток в плоскости чертежа (рис. 3.1).
Согласно принципу суперпозиции магнитных полей,
![]() ,
(3.1)
,
(3.1)
где
![]() – магнитные индукции полей, создаваемых
токами, притекающими по каждой стороне
прямоугольника.
– магнитные индукции полей, создаваемых
токами, притекающими по каждой стороне
прямоугольника.
В точке О пересечения диагоналей прямоугольника все векторы магнитной индукции направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что
![]() .
.
Это позволяет векторное равенство (3.1) заменить скалярным:
![]() .
(3.2)
.
(3.2)
Магнитная индукция поля, создаваемого отрезком 1 прямоугольного проводника с током, равна
![]() .
(3.3)
.
(3.3)
Учитывая,
что
![]() и
и![]() ,
формулу (3.3) можно переписать в виде
,
формулу (3.3) можно переписать в виде
![]() (3.4)
(3.4)
Магнитная индукция поля, создаваемого отрезком 2 прямоугольного проводника с током, будет равна
![]() .
(3.5)
.
(3.5)
С
учетом того, что
![]() ,
формула (3.5) приобретает вид
,
формула (3.5) приобретает вид
![]()
![]() .
(3.6)
.
(3.6)
Заметив, что
![]()
получим
![]() (3.7)
(3.7)
С учетом (3.7) формула (3.2) приобретает вид
![]() .
(3.8)
.
(3.8)
После подстановки числовых значений найдем величину магнитной индукции в точке О:
![]() .
.
Задача 3.2
Бесконечно длинный провод изогнут так, как это изображено на рис. 3.2. Радиус дуги окружности равен 10 см. Определить магнитную индукцию поля, создаваемого в точке О током 100 А, текущим по этому проводу.
|
Дано:
|
Рис. 3.2 |
|
B = ? |
Решение
В соответствии с принципом суперпозиции, индукция магнитного поля в точке О равна
![]()
где
![]() – индукции
магнитных полей, создаваемых током,
протекающим по проводам 1 и 3;
– индукции
магнитных полей, создаваемых током,
протекающим по проводам 1 и 3;
![]() –индукция
магнитного поля части окружности
радиусом R.
–индукция
магнитного поля части окружности
радиусом R.
Так
как точка О лежит на оси провода,
![]() ;
;
![]() .
(3.9)
.
(3.9)
В
точке О векторы индукции
![]() и
и![]() направлены перпендикулярно плоскости
«от нас». По этой причине векторное
равенство (3.9) можно заменить скалярным:
направлены перпендикулярно плоскости
«от нас». По этой причине векторное
равенство (3.9) можно заменить скалярным:
![]() .
(3.10)
.
(3.10)
Магнитное
поле
![]() в точке О
создается четвертой частью кругового
тока, поэтому
в точке О
создается четвертой частью кругового
тока, поэтому
![]() .
(3.11)
.
(3.11)
Магнитную
индукцию проводника
![]() найдем по формуле
найдем по формуле
![]() (3.12)
(3.12)
где
![]() .
.
С учетом формул (3.11), (3.12) формула (3.10) принимает вид
![]() .
.
Произведем вычисления:
![]() .
.
Задача 3.3
По
тонкому стержню длиной 20 см равномерно
распределен заряд 300 нКл. Стержень
вращается с частотой 10 c-1
относительно оси, проходящей перпендикулярно
стержню через его середину. Масса стержня
– 10 г. Определить: 1) магнитный момент,
обусловленный вращением заряженного
стержня; 2) момент импульса стержня
относительно центра вращения; 3) отношение
![]() .
.
|
Дано:
|
Рис. 3.3 |
|
|