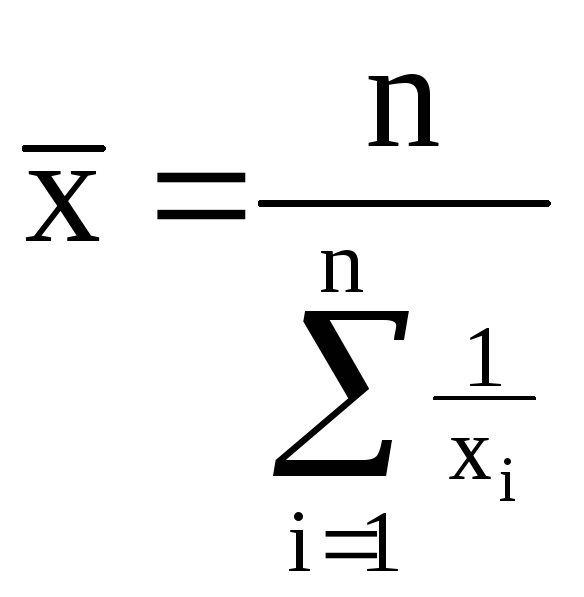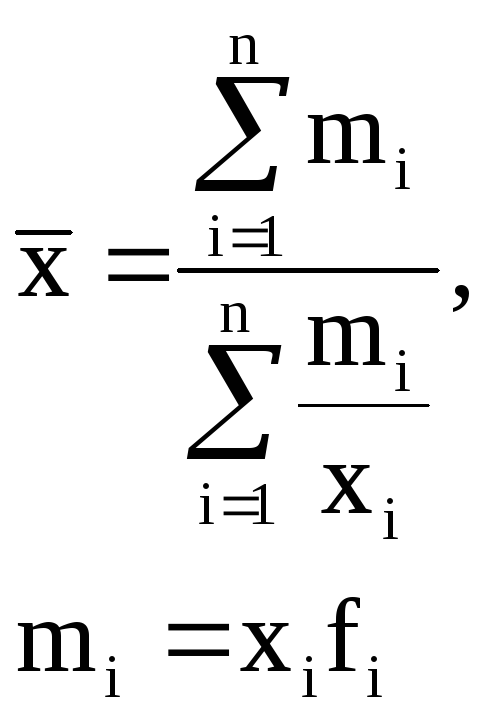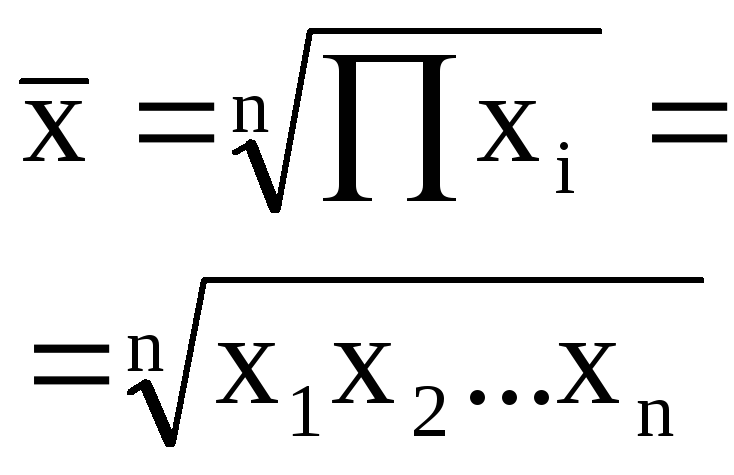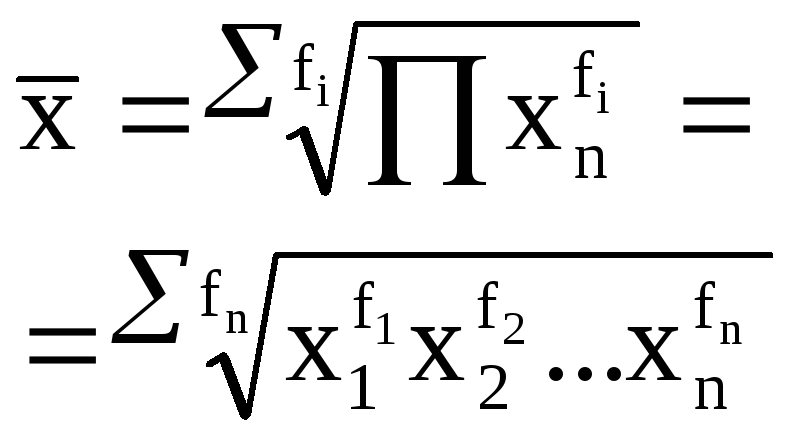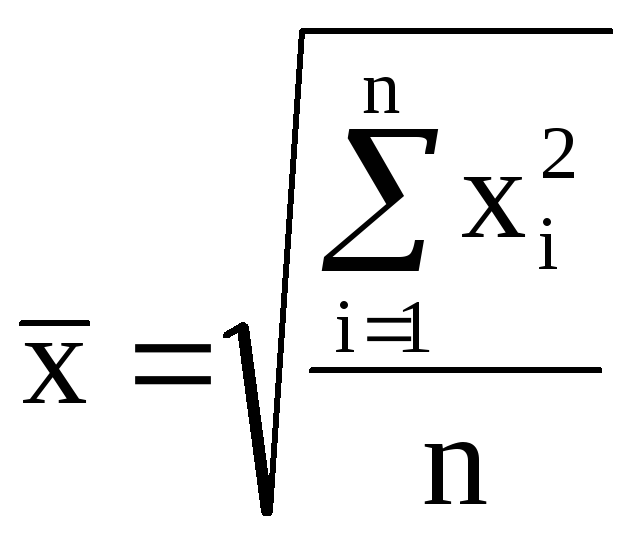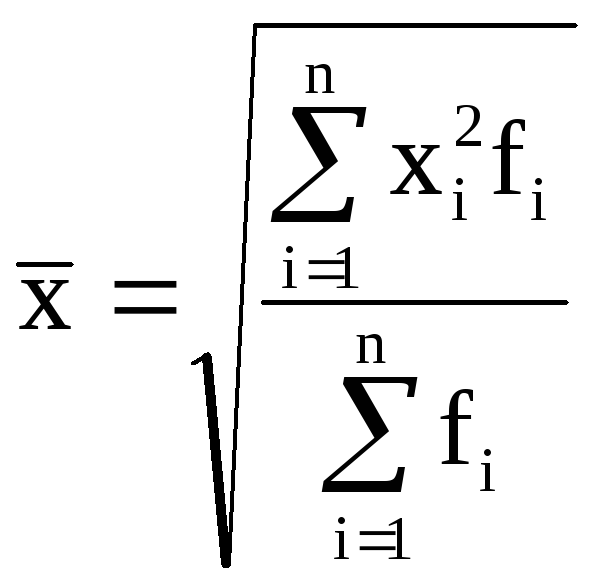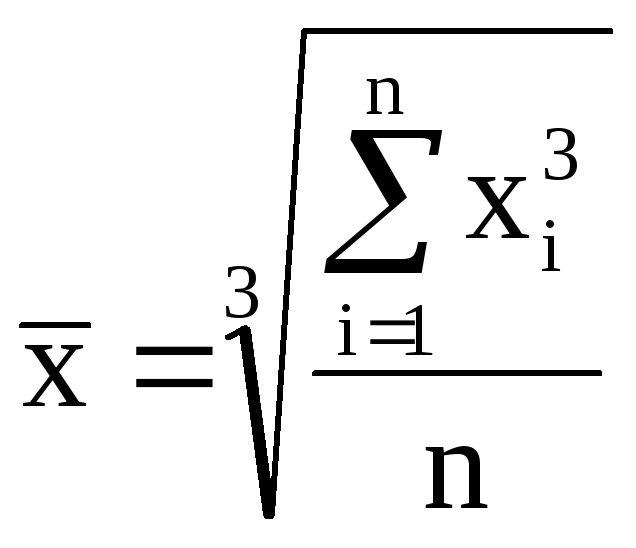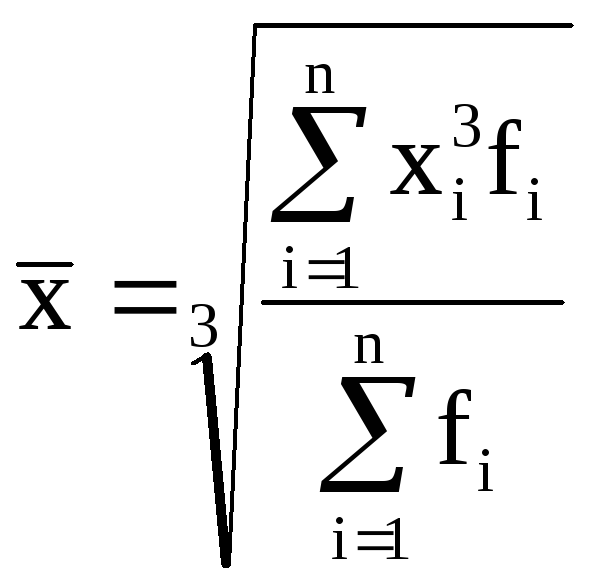2. Классификация средних величин

Средние величины имеют множество форм. В статистике наиболее часто используют степенные и структурные средние. Средние величины классифицируются (рис. 12 ).

Общий вид степенной средней (х):

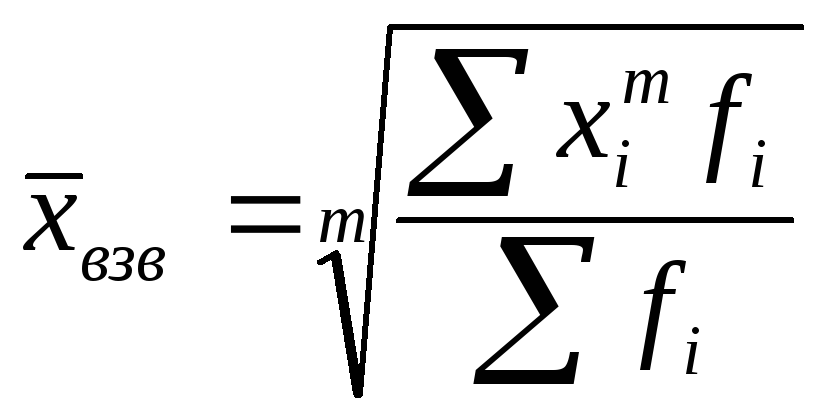, (6.1)

где x_i - варианта (значение) осредняемого признака;

m– показатель степени средней, определяющий ее вид;

n – число вариант; f_i – частота, показывающая, сколько раз встречается i-е значение осредняемого признака.

3. Степенные средние

Каждому значению степени m соответствует определенный вид формулы в табл. 6.1. Средняя величина всегда именованная, имеет ту же размерность, что и признак у отдельных единиц совокупности. Средняя, рассчитанная по совокупности в целом, называется общей средней (), средние, исчисленные для каждой группы, называются групповыми средними (_i). Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, укладывающуюся в конкретных условиях данной группы. Определяющим свойством является способность средних величин сохранять свойства статистических совокупностей.

При выборе вида средней величины обычно исходят из логической сущности осредняемого признака и его взаимосвязи с итоговым показателем.

Весом может быть и частость, т.е. отношение частоты повторения индивидуального значения признака (f_i) к сумме частот (f_i):

(6.2)

Чем больше показатель степени m, тем больше и величина соответствующей средней:

_гарм<_геом<_арифм<_кв<_куб (6.3)

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.

4. Свойства средней арифметической величины

1. Средняя арифметическая постоянной величины равна этой постоянной:

при (6.4)

Пусть

2) Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

(6.5)

Рис. 12 – Классификация средних величин

Таблица 6.1

Характеристики степенных средних

Вид степенной средней	Показатель степени (m)	Формулы расчета
		простая	взвешенная
гармоническая	-1
геометрическая 	0
арифметическая 	1
квадратическая 	2
кубическая 	3

т.к.

3) Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:

(6.6)

т.к.

4) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

(6.7)

5) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю (нулевое свойство):

(6.8)

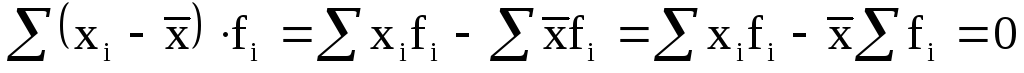6. .Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

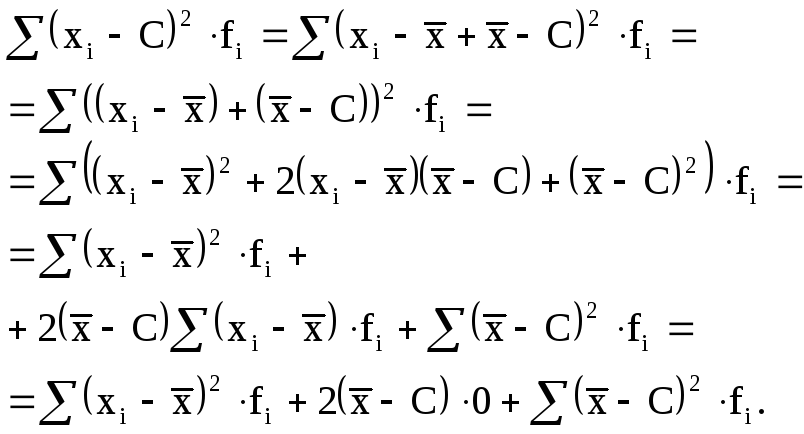(6.9)

7) Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

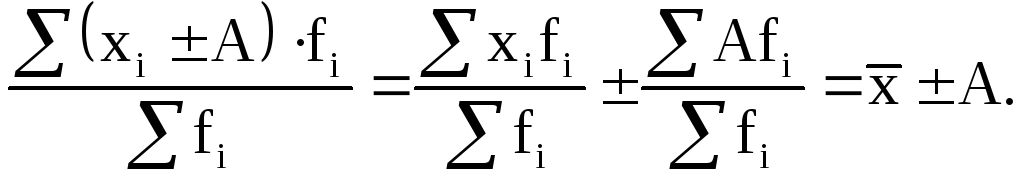(6.10)

8) Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

(6.11)

9) Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

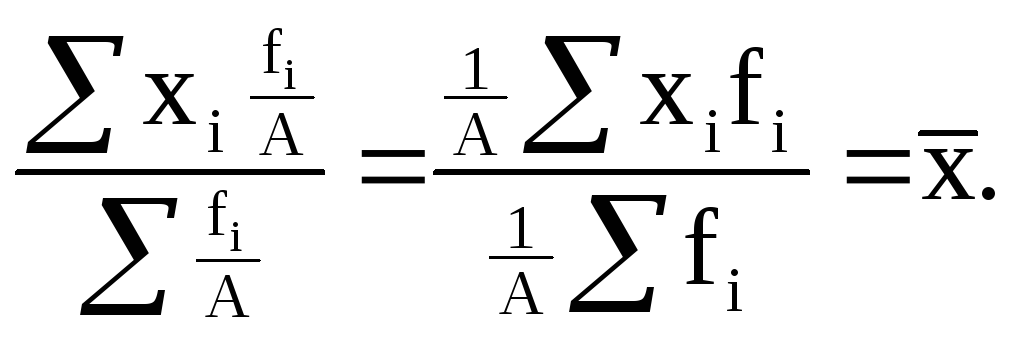(6.12)

При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.

Средняя арифметическая взвешенная по способу моментов:

(6.13)

где х ₀ – условный нуль;

i – величина, на которую делят разность между значениями вариантов и условным нулем (х-х₀);

- момент первого порядка, определяемый по формуле:

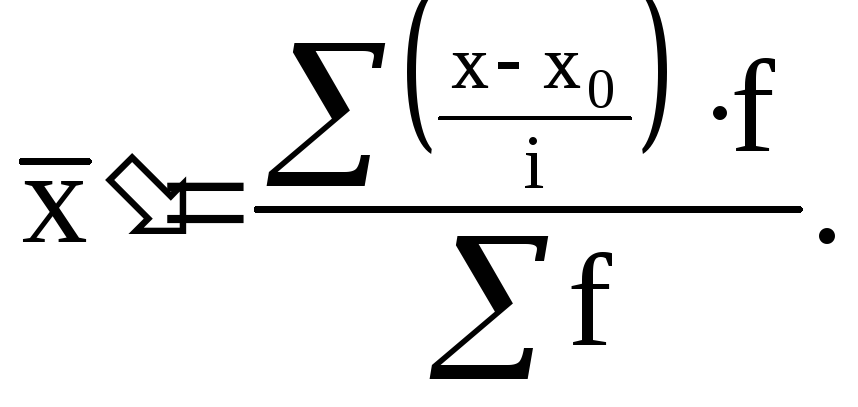(6.14)

Этот способ называют способом отсчета от условного нуля.