3. Лекция №3

3.1. Два метода описания движения жидкостей и газов

В механике существуют два метода изучения движения. Первый метод - метод Лагранжа - заключается в том, что движение частицы изучается наблюдателем, движущимся с этой частицей. В этом случае движение задается положением частиц в функции от времени и от их начальных координат в некоторый момент времени , т.е.

;

; (3.1)

.

Задача сводится к определению траектории движения частицы.

Второй метод - метод Эйлера - заключается в том, что движение среды изучается наблюдателем, расположенным в неподвижной точке. В этом случае движение среды определяется скоростями частиц в зависимости от времени и координат точек пространства х, у и z, относительно которых происходит движение, т.е.

(3.2)

или в проекциях

;

; (3.3)

.

3.2. Понятие о линиях и трубках тока. Ускорение жидкой частицы

В кинематике сплошных сред изучается движение деформируемых тел. Деформируемость является главной кинематической особенностью сплошных сред вообще и жидкостей и газов в частности.

Будем считать, что все кинематические величины непрерывны в пространстве и времени и дифференцируемы.

Движение сплошных сред характеризуется, прежде всего, скоростями ее частиц. В каждый момент времени каждая частица имеет определенную по величине и по направлению скорость. Картина скоростей в данный момент времени называется полем скоростей.

Если поле скоростей остается неизменным во времени, то движение называется стационарным, или установившимся. Если же оно зависит от времени, то движение будет нестационарным.

В практике часто пользуются понятиями средних скоростей. Обычно усреднение скорости производится либо по времени, либо по площади некоторого сечения потока.

Среднее значение величины скорости за промежуток времени представляет собой интеграл в виде

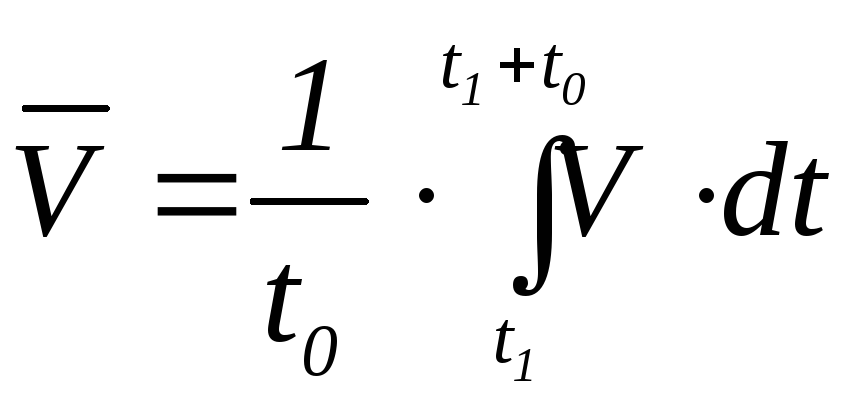. (3.4)

Средняя величина скорости по некоторой площади s определяется следующим образом:

. (3.5)

Вектор ускорения жидкой частицы, движущейся со скоростью V, является индивидуальной производной по времени от вектора скорости, т.е.

. (3.6)

Так как вектор скорости в общем случае зависит от времени и координат, т.е.

, (3.7)

то по правилу дифференцирования сложной функции найдем

, (3.8)

но производные от координат движущейся точки по времени есть соответствующие проекции скоростей, т.е.

. (3.9)

Тогда получим

. (3.10)

Первое слагаемое правой части равенства выражает изменение скорости во времени в некоторой фиксированной точке пространства, т.е, местное изменение, и поэтому называется локальной составляющей ускорения. Остальная часть ускорения характеризует изменение скорости частицы при ее перемещении и называется конвективной составляющей ускорения.

В проекциях на оси координат х, у и z уравнение (3.10) будет иметь вид

;

; (3.11)

.

При изучении векторных полей, встречающихся в механике сплошных сред, пользуются некоторыми характерными линиями и поверхностями. Прежде чем перейти к их определению, рассмотрим некоторые общие понятия, относящиеся к любым векторным полям.

Векторной линией в поле векторов называется линия, в каждой точке которой в данный момент времени вектор касателен к ней. Совокупность векторных линий, проходящих через все точки некоторого контура, образуют векторную поверхность. Если контур, через все точки которого проходят векторные линии, замкнутый, то часть пространства, заключенная внутри векторной поверхности, образует векторную трубку.

Исходя из определения векторной линии, нетрудно получить ее уравнение. Так как в каждой точке контура (рис. 3.1) вектор а касателен к контуру, то, следовательно, вектор а и элементарный вектор dr совпадают по направлению и их векторное произведение равно нулю

.

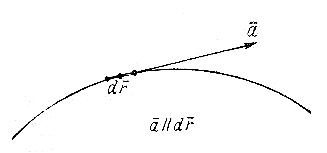
Рис. 3.1. Векторная линия

Из условия равенства нулю проекций этого векторного произведения следует, что

. (3.12)

Приведенные понятия можно применить к любым векторным полям. Применительно к наиболее распространенному в механике сплошных сред и гидромеханике векторному полю - полю скоростей - векторная линия называется линией тока, а векторная трубка - трубкой тока (рис. 3.2).

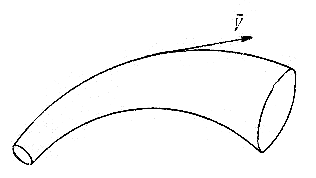
Рис. 3.2. Трубка тока

Очевидно, уравнение линии тока будет

. (3.13)

Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Потоки конечных, размеров будем сначала рассматривать как совокупности элементарных струек, т.е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по, другой, но не будут перемешиваться одна с другой.

Элементарная струйка обладает тремя свойствами:

- форма элементарной струйки со временем не изменяется;

- скорости и давления в поперечных сечениях элементарной струйки есть величины постоянные;

- боковая поверхность элементарной струйки не проницаема.

Так как трубка тока образована совокупностью линий тока, то очевидно, что количество вещества, протекающего в любом сечении трубки, будет одним и тем же.

Если рассматривать движение жидкой частицы во времени, то линия, по которой двигалась частица в некоторый промежуток времени, называется траекторией. Для стационарного движения линия тока и траектория совпадают, при нестационарном движении они отличаются друг от друга.

Через любую точку движущей среды в данный момент времени можно провести лишь одну линию тока, но существуют некоторые особые точки, в которых это правило нарушается. В особых точках линии тока пересекаются и величина скорости должна быть равна либо нулю, либо бесконечности.

При обтекании тела так называемая нулевая линия тока, образующая непроницаемый контур тела, имеет особые точки. В этих точках, называемых критическими, величина скорости равна нулю.

Особая точка другого типа получается при рассмотрении задачи о вытекании среды из одной точки или, наоборот, при ее втекании в точку.

Первое движение будем называть точечным источником, а второе - стоком. В обоих случаях в точках пересечения линий тока величина скорости обращается в бесконечность.