4.3. Напряжения поверхностных сил

Поверхностные силы, действующие в движущихся сплошных средах, существенно отличаются от поверхностных сил, действующих в покоящейся среде. Это отличие заключается не только в появлении касательных составляющих, которые в покоящейся жидкости отсутствуют, а также и в том, что нормальные составляющие сил изменяют свою величину. Найдем величины, определяющие поверхностные напряжения в некоторой точке сплошной среды. Для этого рассмотрим в движущейся жидкости элементарный тетраэдр с вершиной в точке О (рис. 4.2).

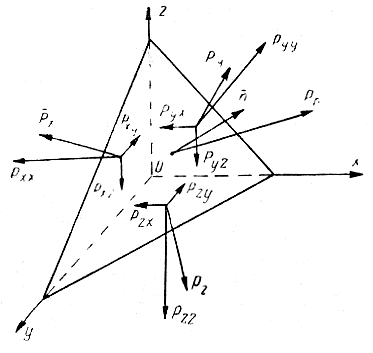
Рис. 4.2. Расчетная схема элементарного тетраэдра

Площади боковых граней тетраэдра равны , причем индексы означают ось, перпендикулярно которой расположена грань. Наклонная грань имеет площадь, равную ; n - нормаль к этой грани. К каждой из рассматриваемых граней будут приложены поверхностные силы, в общем случае направленные под некоторым углом к грани. Обозначим вектор напряжения поверхностных сил, приложенных к грани, перпендикулярной оси х, через соответственно к граням, нормальным к осяму и z, через и. К наклонной грани приложено напряжение.Как видно из рис. 4.2

;

; (4.7)

.

Второй индекс у проекций напряжений означает ось, на которую проектируются векторы напряжений ,и.

Зная ,и, можно определить вектор поверхностных сил , приложенный к площадке с любым заданным направлением орта нормалиn.

Действительно, написав уравнение движения центра инерции тетраэдра с массой dm, получим

, (4.8)

где - скорость центра инерции тетраэдра;

F - плотность массовых сил.

Члены в уравнении, содержащие элементарную массу, являются величинами третьего порядка малости, в то время как остальные - второго порядка малости. Поэтому величинами, содержащими dm, пренебрегаем. Получим

. (4.9)

Из рис. 4.2 видно, что

;

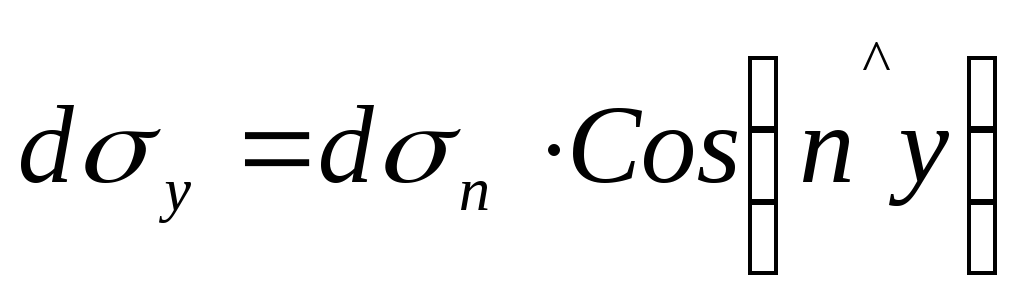; (4.10)

,

поэтому

, (4.11)

где ;

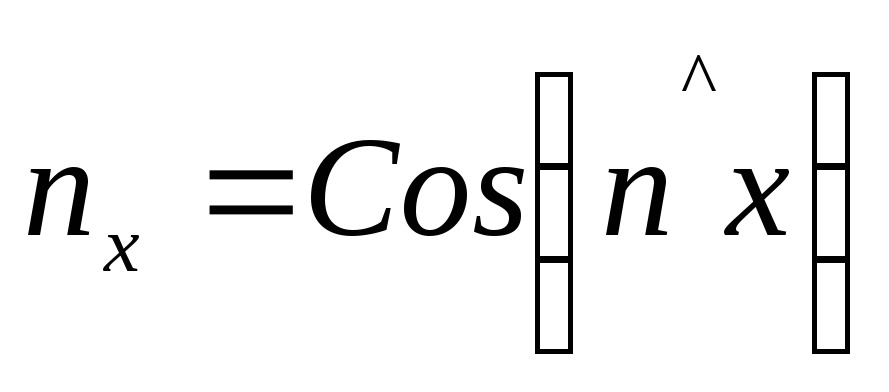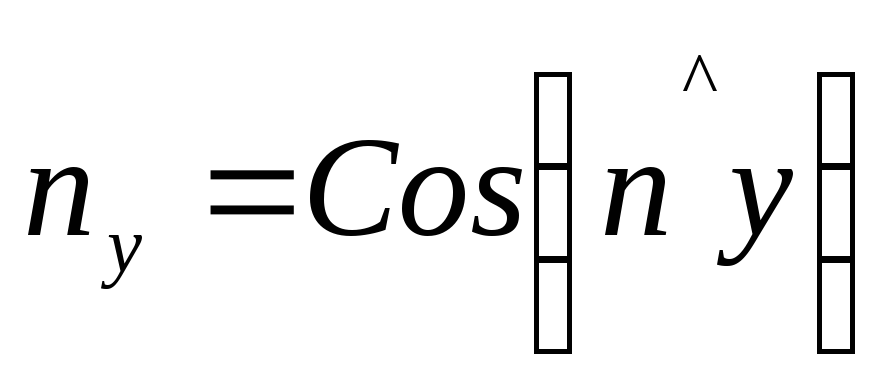; (4.12)

.

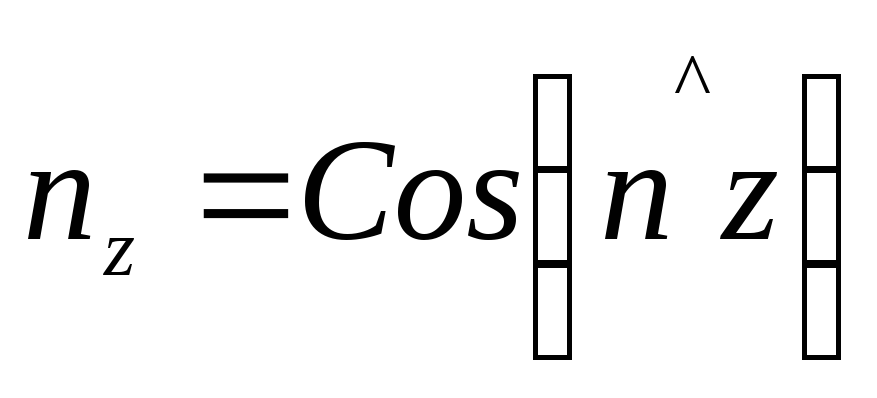Можно получить проекции вектора напряжений поверхностных сил, приложенных к площадке с любым заданным направлением n, на координатные оси х, у и z:

;

; (4.13)

;

Напряжение в точке определяется совокупностью величин

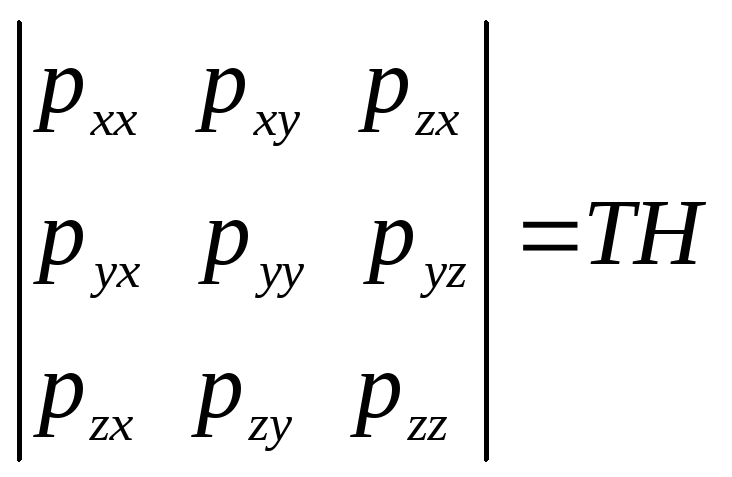. (4.14)

Таблица величин, определяющих напряженное состояние в точке, называется тензором напряжений. Составляющие будем называть компонентами тензора напряжений или просто компонентами напряжений.

4.4. Уравнения движения в напряжениях

Это уравнение можно получить путем применения теоремы об изменении количеств движения к некоторому элементарному объему сплошной среды. В соответствии с ранее сказанным все внешние силы складываются из массовых и поверхностных. Следовательно, главный вектор внешних сил можно представить как сумму двух указанных главных векторов сил: объемных и поверхностных . Тогда в соответствии с теоремой об изменении количеств движения получим

. (4.15)

Но , (4.16)

так как есть масса жидкости в объеме , которая остается постоянной во все время движения.

Используя последнее соотношение, получим выражение известного в механике принципа Даламбера

, (4.17)

согласно которому уравнение динамики можно свести к уравнению статики, если к внешним силам присоединить силы инерции.

Применим теорему об изменении количеств движения к массе, заключенной в объеме элементарного параллелепипеда со сторонами dx, dy и dz. Тогда вектор массовых сил можно представить в виде

, (4.18)

где - вектор массовых сил, отнесенный к единице массы.

Найдем теперь главный вектор поверхностных сил. На рис. 4.3 показаны напряжения поверхностных сил, приложенных к граням, нормальным к оси х. Легко показать аналогичную схему напряжений, приложенных к граням, нормальным к осям у и z.

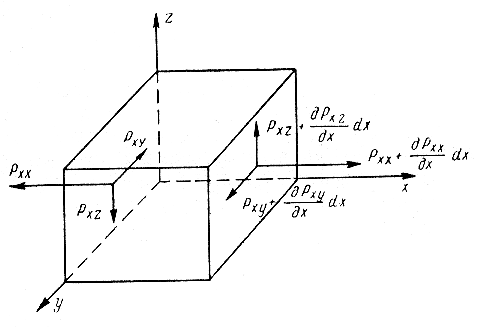
Рис. 4.3. Схема напряжений поверхностных сил

Спроектируем составляющие поверхностных сил на ось х. Рассмотрение сил, приложенных к граням, нормальным к оси х приводит к выражению

, (4.19)

к граням, нормальным к оси у, -

, (4.20)

к граням, нормальным к оси z -

. (4.21)

Таким образом, проекция главного вектора поверхностных сил на ось х будет

. (4.22)

Соответственно проектирование на оси у и z дает

; (4.23)

. (4.24)

Тогда в соответствии с формулой получим уравнения, отнесенные к единице объема, в проекциях на прямоугольную систему координат

; (4.25)

; (4.26)

. (4.27)

Так как вектора напряжений поверхностных сил и, приложенных к площадкам, нормальным осямх, у и z, равны

; (4.28)

; (4.29)

, (4.30)

то уравнение в векторном виде будет

. (4.31)

Эти уравнения являются уравнениями движения сплошных сред в напряжениях; в дальнейшем их будем называть уравнениями в напряжениях.