5.3. Уравнение Навье-Стокса для вязкой жидкости

Рассмотрим изотермическое движение вязкой несжимаемой жидкости. В этом случае плотность и вязкость будут величинами постоянными.

Подставим выражения компонент напряжений в соответствии с формулами (5.20) - (5.22) и (5.29) в уравнения в напряжениях (4.31) и, учитывая, что для несжимаемой жидкости

, (5.30)

получим уравнение движения вязкой несжимаемой жидкости. Так, для проекции на ось х найдем

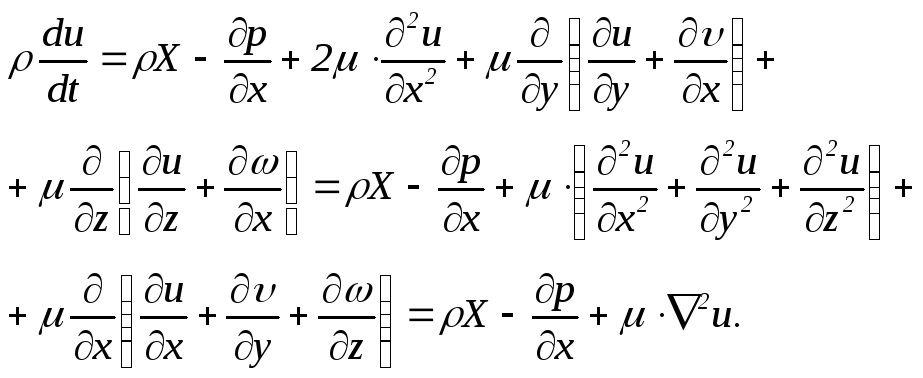(5.31)

Проделав аналогичные преобразования с двумя другими уравнениями (4.31), будем иметь систему уравнений

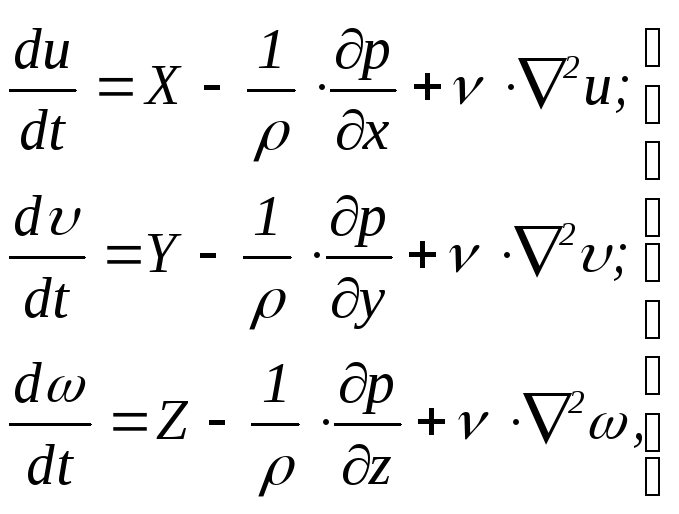(5.32)

где - оператор Лапласа.

Уравнения (5.32) представляют собой замкнутую систему с четырьмя неизвестными ир. Величины и, а также проекции массовых сил X, У и Z должны быть заданы.

Вспоминая выражение для ускорения (3.10), видим, что уравнения (5.32) представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. В векторной форме они имеют вид

, (5.33)

где - вектор с проекциями и.

Уравнения (5.32) впервые были получены в 1845 г. Стоксом и поэтому часто называются уравнениями Стокса.

Для решения системы (5.32) следует задать граничные условия. При наличии же локальных составляющих ускорения, т.е. в нестационарном потоке, необходимы и начальные условия.

Начальные условия ставятся так же, как и для идеальной жидкости, в виде распределения скоростей во всей рассматриваемой области в момент времени , т.е. задается вид функций

.

Граничные условия задаются на поверхности обтекаемого тела и на бесконечности, в невозмущенной жидкости. На бесконечности, как правило, считают известными величины скорости и давления, а для внутренней задачи - расход жидкости.

Тип граничных условий для любого уравнения в частных производных, называют именами известных ученых: Дирихле, Неймана или Робина.

Условие Дирихле соответствует случаю, когда на границе замкнутой области задано значение искомой функции, т.е. и = f. Если на границе замкнутой области задано значение не самой искомой функции, а лишь ее производной по нормали, т.е. ди/дп= f , то такое граничное условие называют условием Неймана. Смешанные граничные условия Дирихле и Неймана в виде ди / дп + ku = f , где k > 0, носят название граничного условия Робина.

6. Лекция №6

6.1. Модель идеальной (невязкой) жидкости. Уравнения Эйлера

Из всех моделей жидкости, рассматриваемых в гидромеханике, наиболее простой является модель идеальной жидкости. Идеальной жидкостью называют жидкость, в которой отсутствуют внутреннее трение и теплопроводность. Таким образом, при движении идеальной жидкости касательных сил трения нет и все взаимодействие между соприкасающимися объемами жидкости сводится к действию нормальных поверхностных сил.

Допущение об отсутствии касательных поверхностных сил означает, что недиагональные компоненты напряжений в точке движущейся жидкости обращаются в нуль

.

Таким образом принимают, что при движении идеальной жидкости, так же как при состоянии равновесия любой сплошной среды, нормальное напряжение в данной точке не зависит от направления площадки, к которой оно приложено.

В гидростатике и гидродинамике скалярную величину нормального напряжения давления в данной точке потока идеальной жидкости будем называть гидродинамическим давлением или давлением в данной точке.

Несмотря на то, что идеальная жидкость в действительности не существует, многие теоретические решения, полученные в предположении идеальности жидкости, имеют большое практическое значение.

Это объясняется тем, что идеальная жидкость сохраняет основные свойства реальных жидкостей (непрерывность или сплошность).

Для вывода уравнения движения воспользуемся уравнением в напряжениях, проекция которого на ось х будет

(6.1)

где - проекция ускорения;

- проекция массовой силы, отнесенной к единице объема.

Остальные три слагаемых представляют собой производные от нормальных и касательных напряжений в жидкости.

Так как в идеальной жидкости вязкость отсутствует, а касательные напряжения равны нулю, то величина нормальных напряжений будет . Поэтому уравнения движения идеальной жидкости в проекциях на оси координат имеют вид

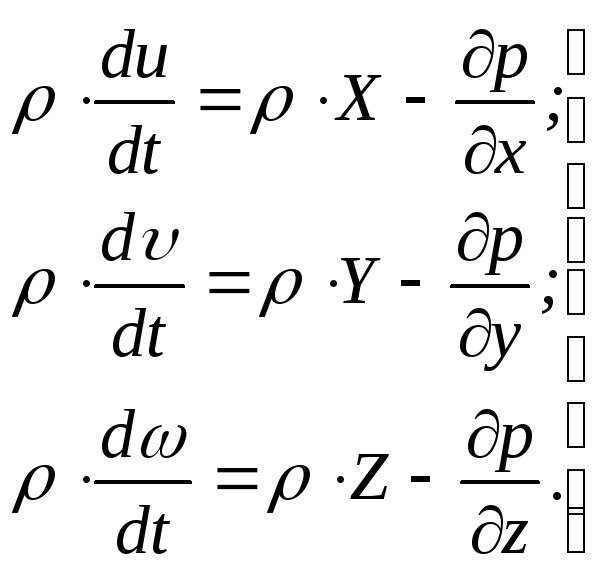(6.2)

Полученную систему уравнений в векторной форме можно представить в виде

. (6.3)

Это уравнение движения идеальной жидкости часто называют уравнением Эйлера.

В общем случае скорость движения жидкости зависит как от координат, так и от времени, поэтому

. (6.4)

Подставив соответственно выражение для ив уравнение (6.2), получим следующий вид дифференциальных уравнений движения (уравнений Эйлера)

(6.5)

Для интегрирования дифференциальных уравнений движения необходимо иметь некоторые начальные и граничные условия.

Преобразуем левую часть уравнения Эйлера. Ускорение жидкости в проекции на ось х записывалось в уравнении Эйлера в виде

Добавлением и вычитанием величины этому выражению можно придать вид

. (6.6)

Так как

(6.7)

и

, (6.8)

то левая часть уравнения Эйлера будет иметь вид

, (6.9)

где - проекция векторного произведения двух векторов на осьx.

Преобразуя аналогично остальные уравнения Эйлера, запишем уравнения движения идеальной жидкости в форме Громека

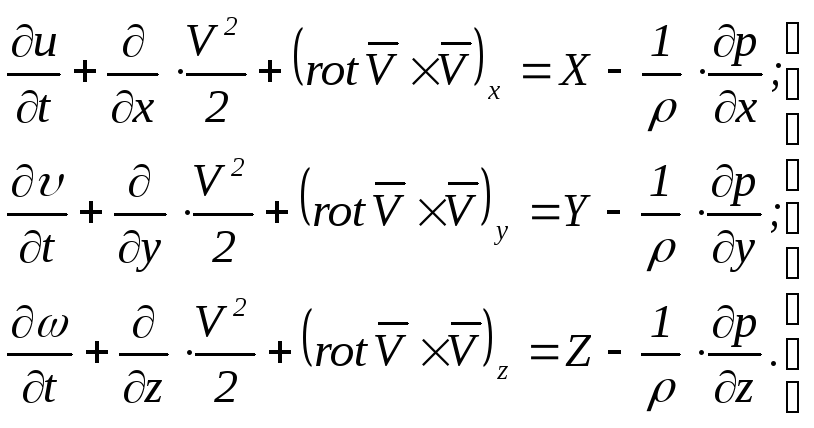(6.10)

Особенность уравнения Эйлера в форме Громека заключается в выделении в явном виде члена, содержащего вихрь вектора скорости. При равенстве нулю слагаемого система уравнений (6.10) сильно упрощается и нетрудно получить интеграл этого уравнения. Последнее слагаемое обращается в нуль в трех случаях: 1) скорость потока равна нулю; 2) векторы скорости и вихря скорости параллельны и поэтому векторное произведение равно нулю. Это случай так называемого винтового движения, весьма редко встречающегося в практике; 3) вихрь скорости равен нулю. Это - безвихревой или так называемый потенциальный поток.