17. Понятие несобственного интеграла I рода

Пусть функция непрерывна на промежутке. Если существует конечный пределто его называют несобственным интегралом первого рода и обозначают.

Таким образом, по определению

В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интегралрасходится.

Аналогично определяется несобственный интеграл на промежутке :

Несобственный интеграл с двумя бесконечными пределами определяется формулой

где c – произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Если непрерывная функция на промежуткеи интегралсходится, то он выражает площадь бесконечно длинной криволинейной трапеции

18. Понятие несобственного интеграла II рода

Пусть функция непрерывна на промежуткеи имеет бесконечный разрыв приx=b. Если существует конечный предел то его называют несобственным интегралом второго рода и обозначают. Таким образом, по определению,Если предел в правой части существует, то несобственный интегралсходится. Если же указанный предел не существует или он бесконечен, то говорят, что интегралрасходится. Аналогично, если функциятерпит бесконечный разрыв в точкеx=a, то полагают

Е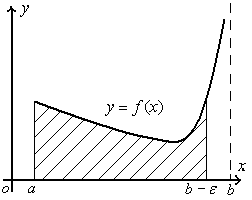сли функциятерпит разрыв во внутренней точкеc отрезка , то несобственный интеграл второго рода определяется формулойВ этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся. В случае, когда, несобственный интеграл второго рода(разрыв в точкеx=b) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции.

19. 20. Признаки сравнения (для несобственного интеграла I и II рода.)

Для несобственного интеграла I рода

Теорема1. Первый признак сравнения: Путь заданы две непрерывные функции f(x) и g(x), неотрицательные на [a,+∞) и 0<=f(x)<=g(x) x[a,+∞).

Тогда 1) если – сходится, тотоже сходится.

2) если - расходится, то- расходится.

Теорема2. Предельный признак сравнения. Если существует предел , ( и ), то интегралыиодновременно оба сходятся или оба расходятся.

Для несобственного интеграла II рода

Терема3: Пусть в левой(правой) окрестности точки b (точки а) определены неотрицательные функции f(x) и g(x), причем 0<=f(x)<=g(x).

Тогда 1) из сходимости н.и. 2 рода - сходится

2) из расходимости н.и. расходится

Теорема4. (Предельный признак сравнения) Пусть f(x) и g(x) неотрицательные, и g(x)0 на промежутке [a,b), а в точке b функция терпит разрыв. Если существует , , то интегралы иодновременно сходятся или одновременно расходятся.

21. Свойства определенного интеграла от чет. И нечт. Функции на симметричном промежутке.

Если функция f(x) чётная на отрезке [-a;a], то

Если функция f(x) нечётная на отрезке [-a;a], то

22. Понятие общего решения дифференциального уравнения первого порядка, частное решение, начальные условия, задача Коши.

Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение (2), что:

1. Любое решение (2) относительно y (для набора постоянных C₁, C₂, …, C_n из некоторой области n-мерного пространства) - частное решение уравнения (1); 2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C₁, C₂, …, C_n. Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной: (3) и получать общее решение в форме (4) решённой относительно неизвестной функции.

Опр. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. Так, функция y(x) = e^x + x обращает уравнение : y⁽⁴⁾ – y + x = 0 в тождество на всей числовой оси (y⁽⁴⁾(x) = e^x; e^x –(e^x +x) + x = 0), т.е. является частным решением этого уравнения. Любое уравнение порядка имеет множество частных решений (частным решением приведённого уравнения является и функция y(x) = sin(x) + x). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.

Задача Коши (задача с начальным условием). Пусть функция f(x, y) определена в области D, точка . Требуется найти решение уравнения ; (8) удовлетворяющее начальному условию y(x₀) = y₀; (9) (начальное условие (9) часто записывают в форме ). Теорема Коши (существования и решения задачи Коши). Если в области D функция f(x, y) непрерывна и имеет непрерывную частную производную , то для любой точки в окрестности точки x₀ существует единственное решение задачи ((8),(9)).