1. Понятие первообразной. Свойства первообразной.

Определение. Функция F(x) называется первообразной функции f(x) на (a;b), если для x (a;b) выполняется равенство F’(x)’=f(x)

Т. (о первообразных). Все первообразные для данной функции отличаются на постоянное слагаемое.

Это значит, что ели F(x) есть какая-либо первообразная для функции f(x), то все бесконечное множество ее первообразных можно записать одним выражением F(x)+C.

Для того, чтобы 2 функции были дифференцируемы на Т или были первообразными одной и той же функции необходимо и достаточно, чтобы на этом промежутке эти 2 функции отличались на константу.

F(x)-G(x)=C

Совокупность всех ее (функция f задана на Т) первообразных называется неопределенным интегралом.

Обозначается

f(x)-подынтегральная функция

f(x)dx-подынтегральное выражение

∫ - знак неопределенного интеграла

2. Понятие неопределенного интеграла. Свойства неопределенного интеграла.

Определение. Неопределенным интегралом от функции f(x) на интервале (a;b) называется совокупность всех ее первообразных.

, где F(x), какая-либо первообразная функции f(x) на (a;b).

f(x) – подынтегральная функция

f(x)dx подытегральная функция

 - знак интеграла.

Свойства неопределенного интеграла.

1. Вынесение постоянного множителя.

Постоянный множитель можно выносить за знак интеграла

2. Почленное интегрирование.

Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых

3. Дифференцирование интеграла.

Производная неопределенного интеграла по переменной интегрирования равна подынтегральной функции

это свойство является единственным критерием проверки правильности результата интегрирования.

4. Символы неопределенного интегрирования и дифференциала, стоящие рядом, взаимно уничтожаются

5. Инвариантность формы

Форма результата интегрирования не зависит от того, что является переменной интегрирования – независимая переменная, или функция U(x) (свойство инвариантности формулы интегрирования).

Т.е. если

3. Методы вычисления неопределенного интеграла: метод подстановки (замены переменной),

формула интегрирования по частям.

1. Непосредственное интегрирование – интегрирование с помощью свойств, тождественных преобразований подынтегральной функции и таблицы основных интегралов.

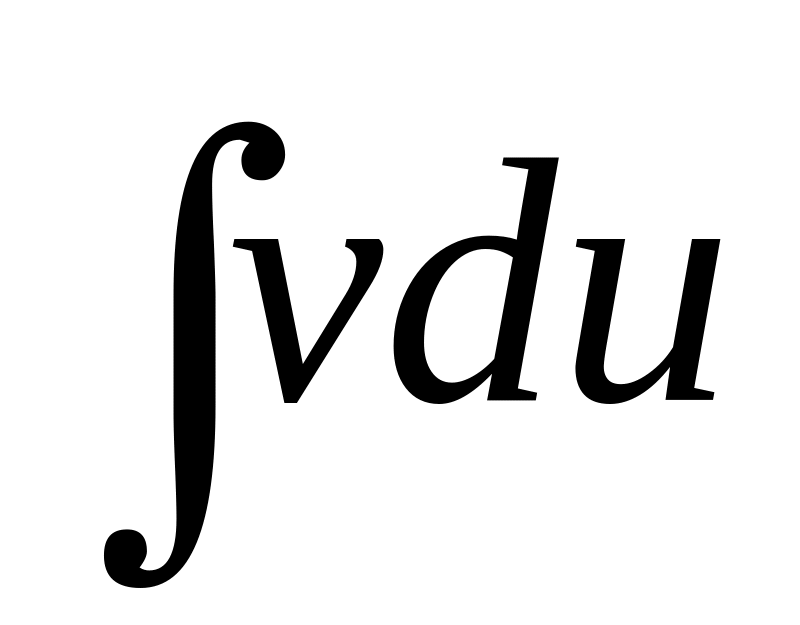
2. И 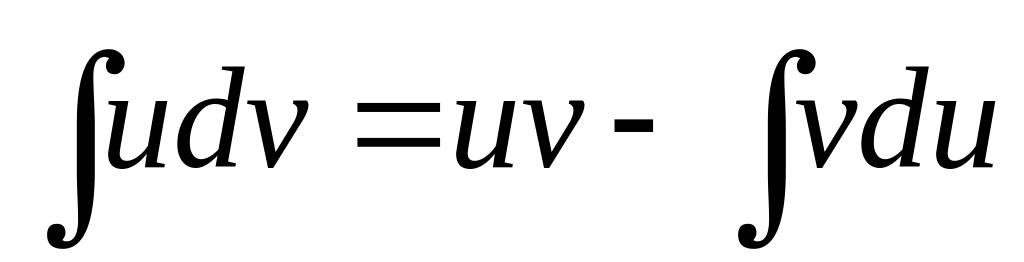нтегрирование по частям. Теорема. Если функции u(x) и v(x) дифференцируемы на некотором промежутке и на этом промежутке существует интеграл , то на нем существует и интеграл , причем

3. Замена переменной. Теорема. Пусть функция x = j(t) определена и дифференцируема на некотором множестве Т и j : Т ® X. Тогда если на множестве X функция y = f (x) имеет первообразную F(x), то на множестве Т функция F(j(t)) является первообразной для функции f (j(t)) j¢ (t). Из теоремы следует, что

.

4.Интегрирование рациональных функций.

1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен.

2. Знаменатель Q_n(x) разложим на простейшие сомножители:

Q_n(x) = (x – a)^k…(x – b)^r (x² + p x + q)^l… (x² + p x + q)^s , где многочлены (x² + p x + q) не имеют действительных корней.

3 . Представим дробь P_m(x) /Q_n(x) в виде суммы простейших дробей с неопределенными коэффициентами:

где A₁, A₂, … ,C_s, D_s неопределенные коэффициенты, которые надо найти.

4. Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.

5. Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях х.

6. Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая x равным действительным корням знаменателя.

7. Подставим найденные коэффициенты A₁, A₂, … ,C_s, D_s в разложение дроби.

8. Проинтегрируем простейшие дроби.

5. Метод неопределенных коэффициентов при разложении дроби на сумму простейших дробей.

Теорема. Пусть P_m(x) /Q_n(x) - правильная рациональная дробь, знаменатель которой представлен в виде произведения линейных и квадратичных множителей (с вещественными коэффициентами)

Q_n(x) = a (x - x₁) ^a (x - x₂) ^b …(x² + p x + q)^l … (x² + r x + s) ^m ,

где x₁, x₂,… - вещественные корни, (x² + p x + q), … (x² + r x + s) - квадратные трехчлены, не разложимые на вещественные множители (a+…+ b+ l +…+ m = n ). Тогда имеет место разложение

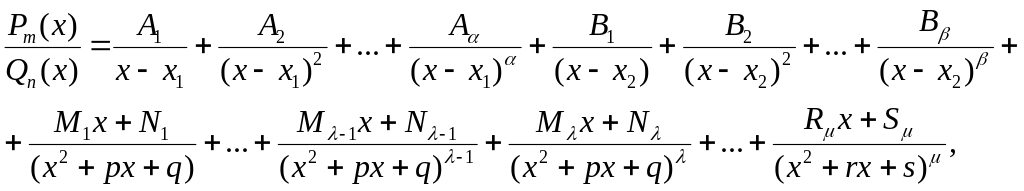
где A_i , B_i , M_i , N_i , R_i , S_i , … - вещественные числа (некоторые из которых могут быть равны нулю).

6. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка

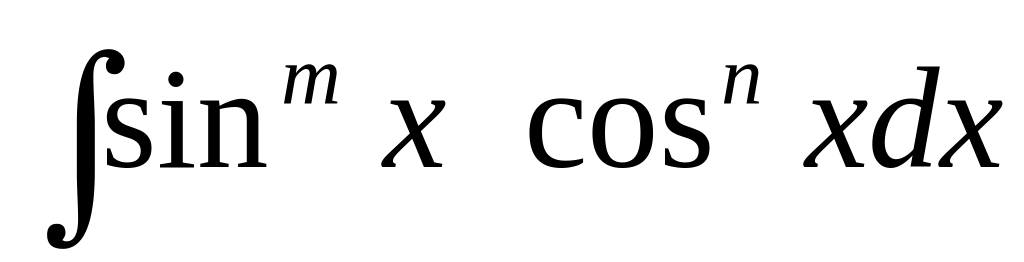2. И нтегралы вида , где n и m – целые.

1. Если n и m – четные, положительные, то применяются формулы понижения степени:

2. Если n или m – нечетное, то непосредственно отделяют от нечетной степени один множитель.

3. Если n и m – дробные или целые отрицательные и (n + m ) четное отрицательное, то замена t = tg x, иди t = сtg x.

у ниверсальная тригонометрическая подстановка

где R – рациональная функция

7. Интегрирование иррациональных функций.

прием выделения полного квадрата и замены полного квадрата на новую переменную

подстановка:

подстановка:

подстановка:

, где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой: , где s – наименьшее общее кратное a, b, g

, где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой: , где s – наименьшее общее кратное a, b, g

Выражение вида где (m,n,p,a,b) – const, называется дифференциальным биномом, интеграл от него решается при помощи подстановки Чебышева.

8. Интегрирование дифференциального бинома. Теорема

И нтеграл вида , где m, n, p – рациональные числа

выражается через элементарные функции только в следующих случаях:

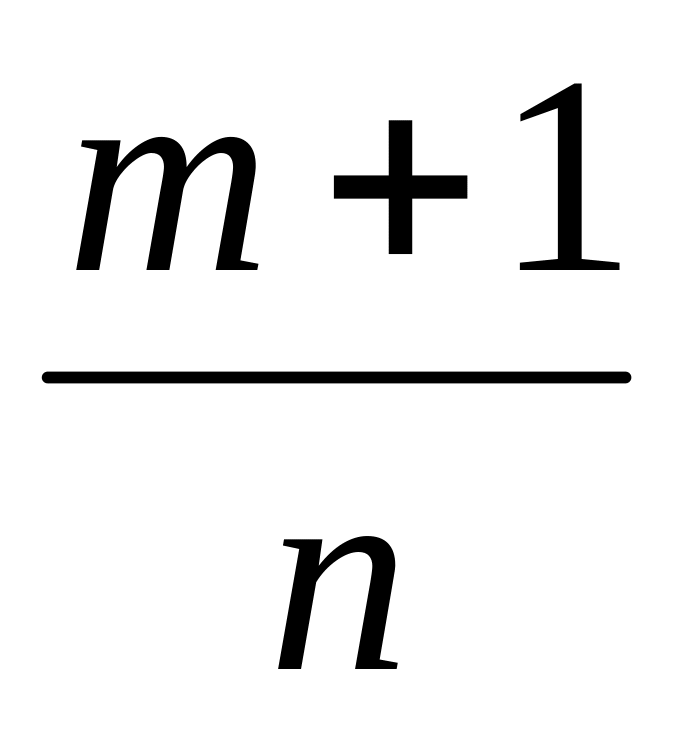
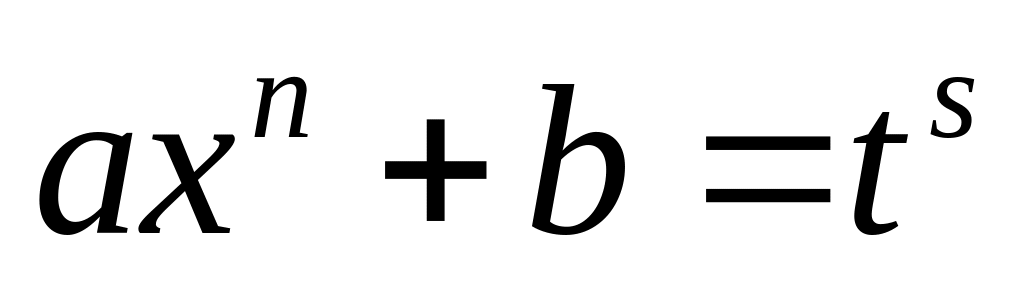1. p < 0 – целое Þ x = t ^s, d x = s t ^s-1 d t , s – нок знаменателей m и n;

2. – целое Þ , s – знаменатель дроби

p = к/s, ;

3. – целое Þ ,

4. s – знаменатель дроби p= к/s,