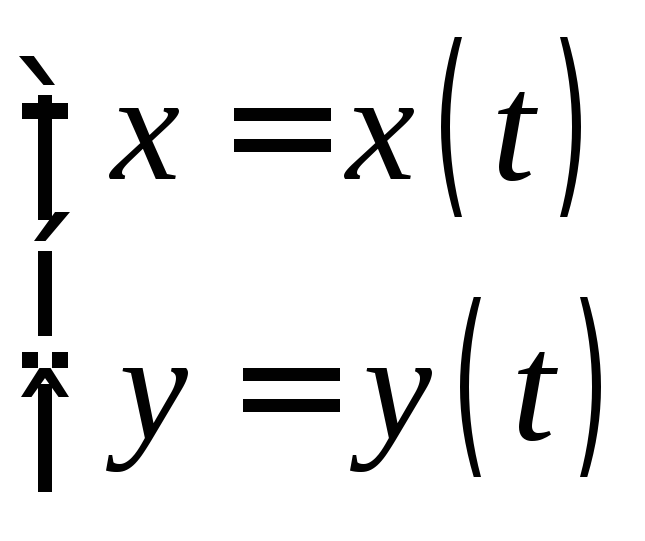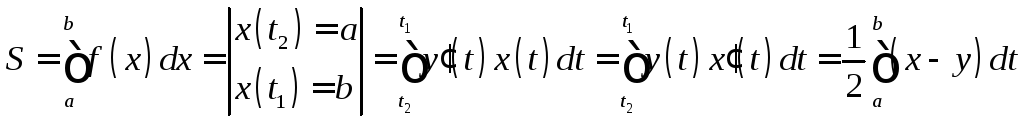ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1. Задача, о площади криволинейной трапеции приводящая к понятию определенного интеграла.

2. Классы интегрируемых функций (три теоремы без док.)

3. Теорема об определенном интеграле с переменным верхним пределом.

4. Теорема Ньютона-Лейбница

5. Теорема об интегрировании по частям

6. Теорема о замене переменной в определенном интеграле.

7. Вывод формулы вычисления площади плоской фигуры.

8. Вывод формулы вычисления длины дуги (в декартовой системе координат).

9. Вывод формулы вычисления объема тела вращения относительно оси Oy.

10. Теорема об абсолютной сходимости несобственного интеграла I рода.

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

11. Сформулируйте и докажите свойства решений ОЛДУ.

12. Теорема о равенстве нулю вронскиана линейно-зависимых функций.

13. Теорема о структуре общего решения ЛОДУ.

14. ЛНДУ n-го порядка. Теорема о структуре общего решения (док. для n=2).

15. Теорема о суперпозиции решений (док. для n=2).

16. Метод вариации произвольных постоянных – метод Лагранжа.

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

17. Необходимый признак сходимости.

18. Критерий сходимости рядов с неотрицательными членами .

19. Признак сравнения для рядов с неотрицательными членами.

20. Признак Даламбера (20).

21. Радикальный признак Коши .

22. Абсолютная и условная сходимость. Дост. признак сходимости знакопеременных рядов.

23. Степенные ряды. Теорема Абеля. Радиус сходимости.

24. Тригонометрический ряд Фурье. Нахождение коэффициентов для ряда Фурье.

25. Тригонометрический ряд Фурье. Нахождение коэффициентов для чет. и нечетных функций.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1. Понятие первообразной. Свойства первообразной.

2. Понятие неопределенного интеграла. Свойства неопределенного интеграла.

3. Методы вычисления неопределенного интеграла.

4. Интегрирование рациональных функций.

5. Метод неопределенных коэффициентов при разложении.

6. Интегрирование тригонометрических функций. Универсальная подстановка.

7. Интегрирование иррациональных функций.

8. Интегрирование дифференциального бинома. Теорема Чебышева.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

9. Понятие интегральной суммы.

10. Понятие определенного интеграла. Геом. смысл определенного интеграла.

11. Необходимый признак интегрируемости функции по Риману. Функция Дирихле.

12. Свойства определенного интеграла. Теорема о среднем.

13. Свойства линейности и аддитивности определенного интеграла.

14. Свойства определенного интеграла, выражаемые неравенствами.

15. Теорема о дифференцировании определенного интеграла с переменным верхним пределом.

16. Объем тела вращения с заданным поперечным сечением.

17. Понятие несобственного интеграла I рода.

18. Понятие несобственного интеграла II рода.

19. Признаки сравнения (для несобственного интеграла I и II рода.)

20. Предельные признаки сравнения (для несобственного интеграла I и II рода.)

21. Свойства определенного интеграла от чет. и нечетной функции на симметричном промежутке.

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

22. Понятия общее решение дифференциального уравнения первого порядка, частное решение, начальные условия, задача Коши.

23. Теорема о существовании и единственности решения ДУ в полных дифференциалах

24. Определитель Вронского.

25. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение.

26. Теорема о существовании и единственности решения задачи Коши для ДУ n-го порядка.

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

27. Числовой ряд. Основные понятия и определения: определение числового ряда, n-ой частичной суммы, сходящегося и расходящегося ряда.

28. Интегральный признак Коши.

29. Знакочередующиеся ряды. Теорема Лейбница.

30. Равномерная сходимость функционального ряда.

31. Теорема Вейерштрасса.

32. Свойства равномерно сходящихся функциональных рядов

33. Ортогональная система функций.

34. Теорема Дирихле. Условия Дирихле.

35. Степенные ряды. Область сходимости. Радиус сходимости.

36. Ряд Тейлора, область сходимости. Достаточный признак сходимости ряда Тейлора.

37. Ряд Маклорена.

38. Тригонометрический ряд Фурье.

1. Задача, о площади криволинейной трапеции приводящая к понятию определенного интеграла.

Криволинейная трапеция – плоская фигура, ограниченная линиями . При этом:непрерывная на.

Разобьем на n частей точками x₁, x₂, … , x_n:

, x₀ = a, x_n = b.

Проведя вертикальные линии из каждой точки . Получим n криволинейных трапеций. Рассмотрим отрезок. Выберем точку. Значение функции в этой точке обозначим заf_i. построим прямоугольник с основанием и высотойf_i.

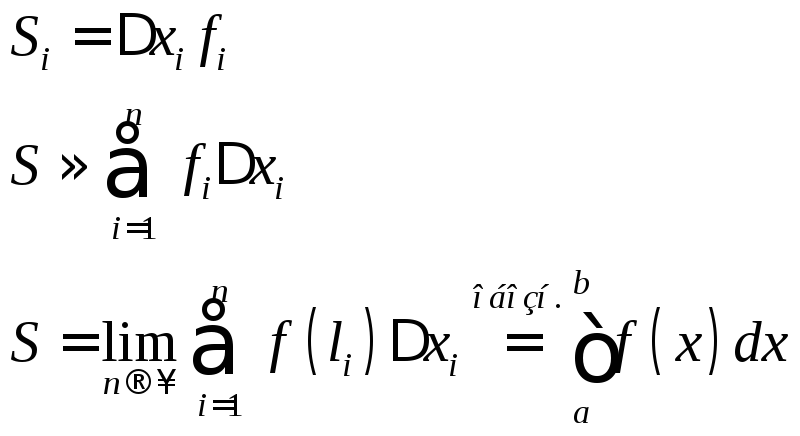
2. Классы интегрируемых функций.

Теорема 1: Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Теорема 2: Если функция ограничена на отрезке и имеет на нём лишь конечное число точек разрыва, то она интегрируема на этом отрезке.

Теорема 3: Если функция монотонна и ограничена на отрезке, то она интегрируема на этом отрезке.

3. Теорема об определенном интеграле с переменным верхним пределом

Теорема:

Определенный интеграл с переменным верхним пределом от функции f(x), непрерывной на [a; b] является первообразной для подынтегральной функции.

Доказательство:

Возьмем и зададим приращение, так, что

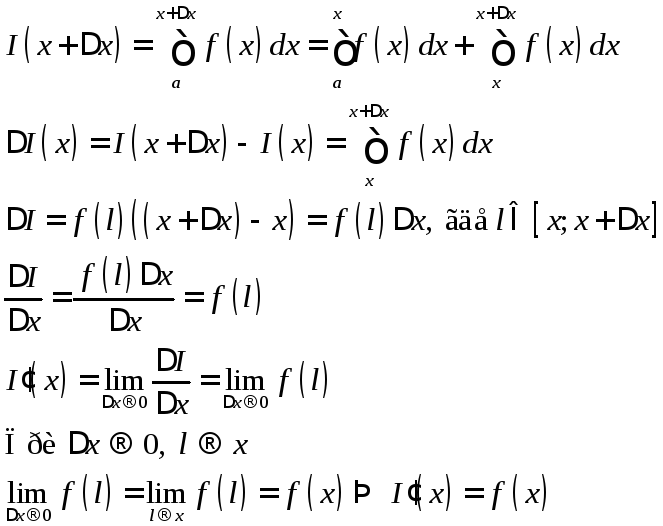
Следствие:

У каждой непрерывной функции есть первообразная.

4. Теорема Лейбница – Ньютона.

Теорема:

Если F(x) – какая-то первообразная для f(x), то справедлива формула:

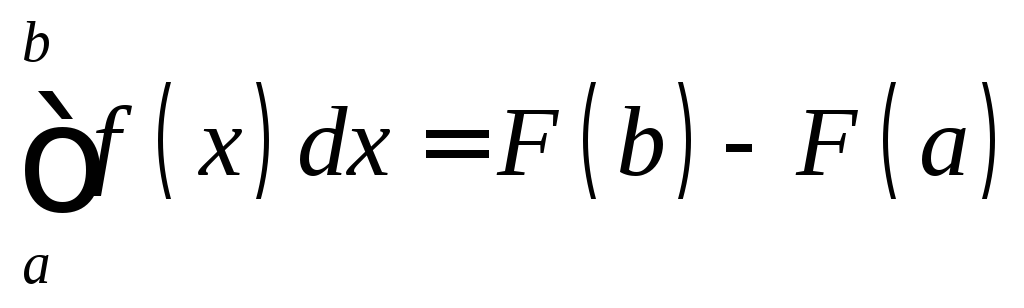
Доказательство:

Пусть F(x) – первообразная для f(x).

По теореме об определенном интеграле с переменным верхним пределом (Определенный интеграл с переменным верхним пределом от функции f(x), непрерывной на [a; b] является первообразной для подынтегральной функции):

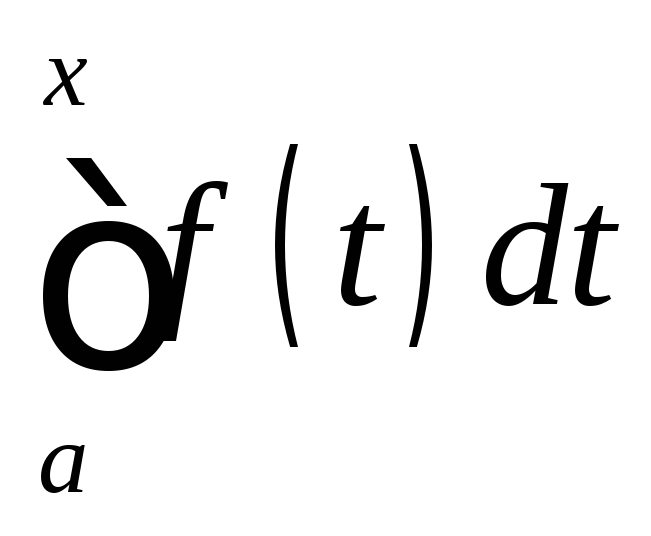–тоже первообразная для f(x).

Две первообразные для f(x) отличаются на C = const. Определим C:

Пусть x = a:

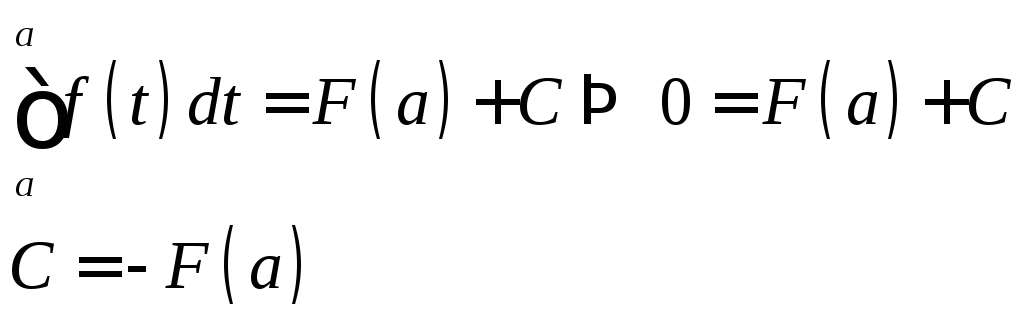
Пусть x = b:

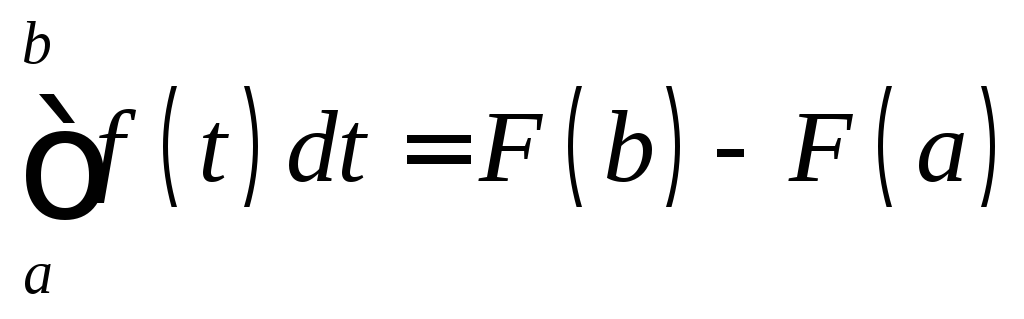
5. Теорема об интегрировании по частям

Теорема:

Пусть функции u(x) и v(x) имеют непрерывные производные на [a; b]. Тогда:

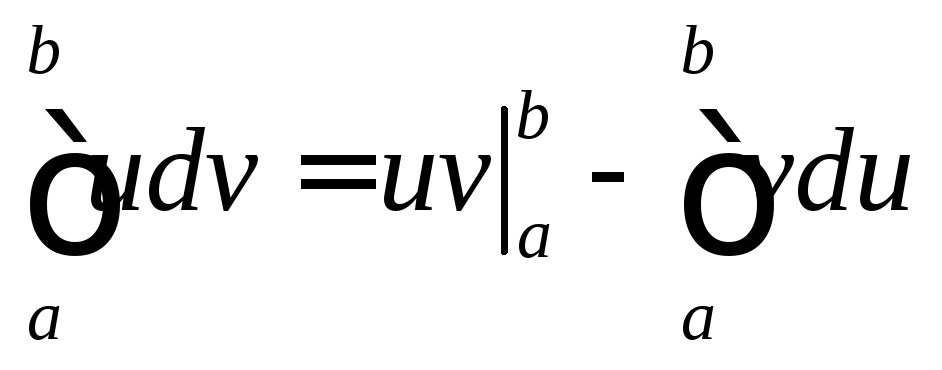
Доказательство:

(uv)’ = u’v + uv’ => uv – первообразная от (u’v+uv’)

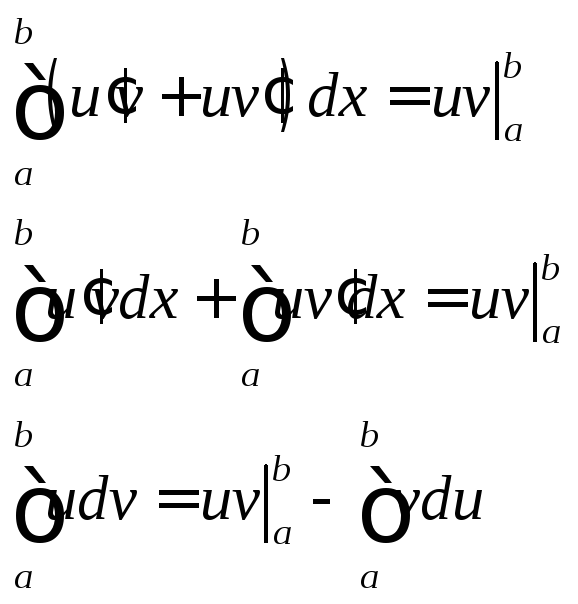
6. Теорема о замене переменной в определенном интеграле

Теорема:

Пусть функция f(x) – непрерывная на [a; b] и функция x = φ(x) – непрерывно дифференцируема на [t₁; t₂], причем φ: [t₁;t₂]→[a; b], и φ(t₁) = a, φ(t₂) = b. Тогда:

Доказательство:

Пусть F(x) – первообразная для f(x) на [a; b]. Тогда:

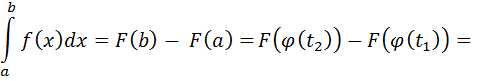
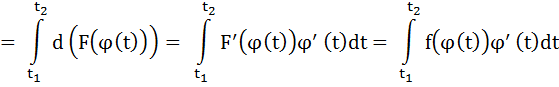
7. Вывод формулы вычисления площади плоской фигуры (в декартовой системе координат)

Плоская фигура – любое ограниченное множество точек плоскости. Если плоская фигура ограничена:

1. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], f(x) ≥ 0 для всех x из отрезка [a; b], x = a, x = b, y = 0

Тогда разобьем на n частей точками x₁, x₂, … , x_n:

, x₀ = a, x_n = b.

Проведя вертикальные линии из каждой точки . Получим n криволинейных трапеций. Рассмотрим отрезок. Выберем точку. Значение функции в этой точке обозначим заf_i. построим прямоугольник с основанием и высотойf_i.

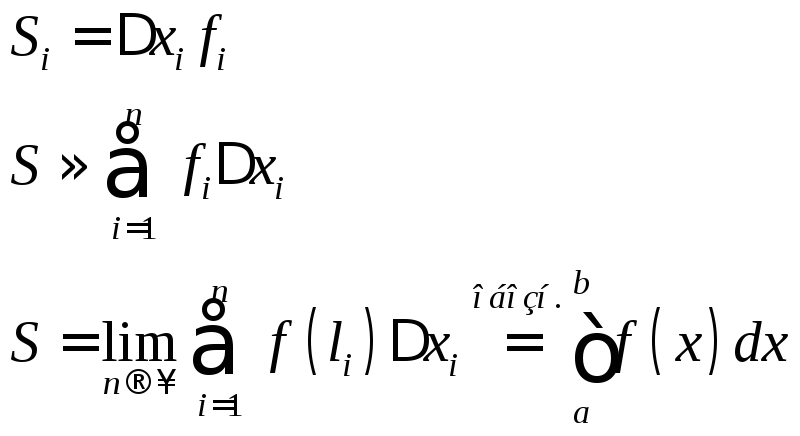
2. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], f(x) ≤ 0 для всех x из отрезка [a; b], x = a, x = b, y = 0

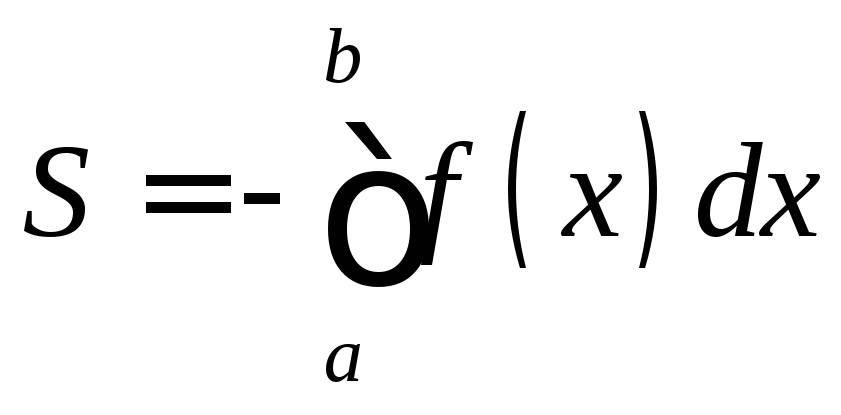
7. Продолжение истории =))

3. Графиком функции f(x), определенной и непрерывной на отрезке [a; b], x = a, x = b, y = 0

4. Двумя графиками f₁(x) и f₂(x) (f₁(x) ≥ f₂(x) для всех x), x = a, x = b

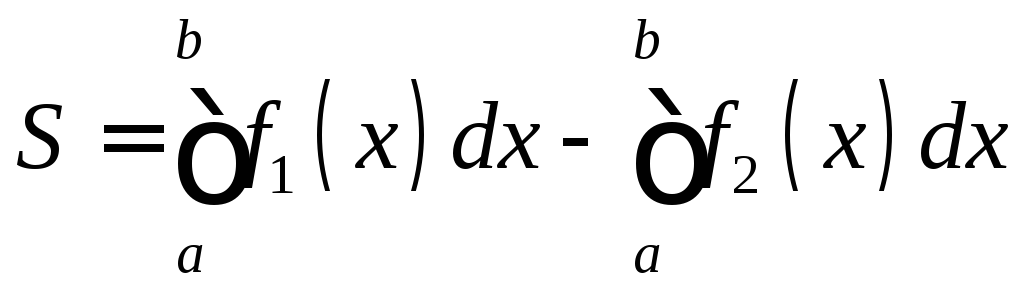
5. Двумя графиками f₁(x) и f₂(x) (общий случай), x = a, x = b

,

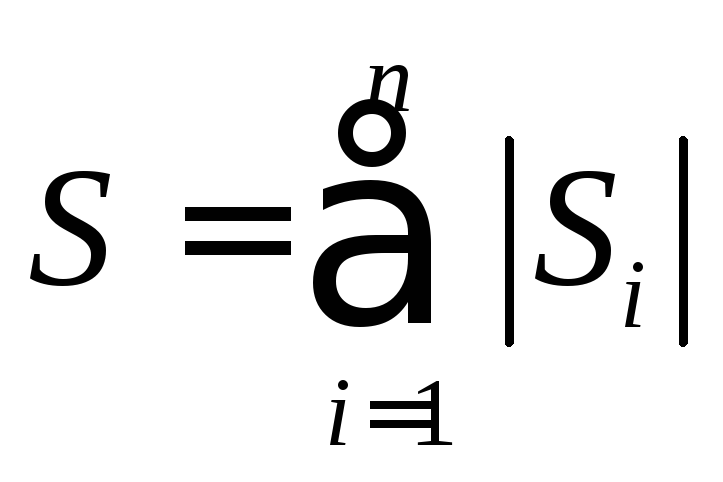где ,

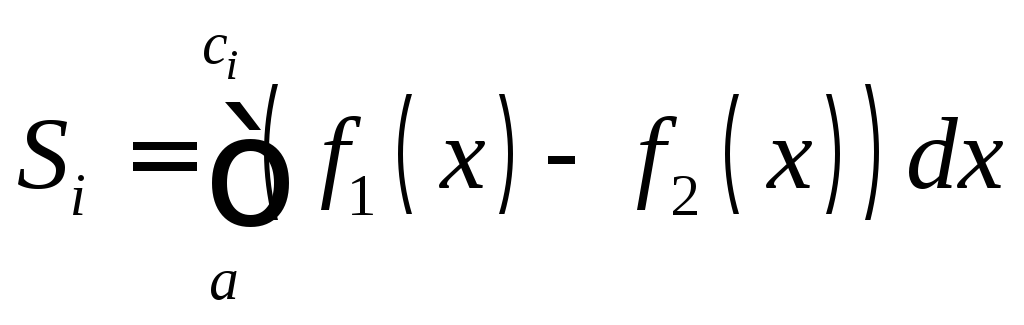где c_i – координата x точки пересечения графиков функций f₁(x) и f₂(x)

6. Простой замкнутой кривой, заданной параметрическим уравнением: