17. Необходимый признак сходимости.

Если числовой ряд сх-ся, то предел его общего члена обязательно равен нулю т.е..

Док-во: Пусть ряд сх-ся. Т.к. ряд сх-ся, то,S_n=a₁+a₂+…+a_n;

S_n-1=a₁+a₂+…+a_n-1.

Поэтому S_n-S_n-1=a_n

)= .

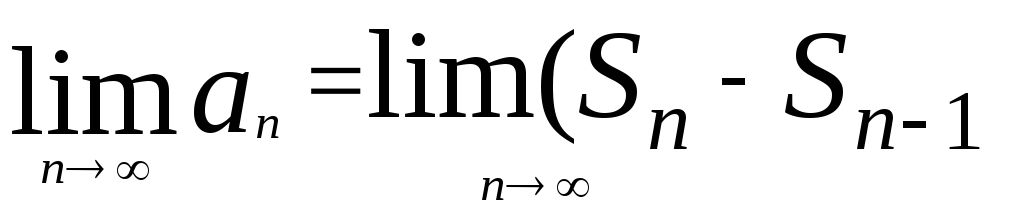Следствие (достаточный признак сх-ти ряда)

Если или не существует, то рядрасходится точно, но, если, то рядможет сходиться, но может и расходится.

18. Критерий сходимости рядов с неотрицательными членами.

Пусть - ряд с неотрицательными членами. Для того чтобы ряд сх-ся => и <= чтобы его частные суммы были ограничены сверху(т.е.Мn S_n M)

Доказательство:

По теореме Вейерштрассе, если монотонна и ограничена, то

1) -монотонно возрастает(т.к.)

2) по предположению(ограничена)

(по усл.Теоремы) =ряд сходится.

19. Предельный признак сравнения для рядов с неотрицательными членами.

Пусть имеется два знакоположительных ряда и.Пусть существует и_{. Тогда эти ряды сходятся или расходятся одновременно.}

Доказательство:

По условию Ǝ N(Ɛ);n>N(Ɛ)

Рассматривая модуль получим ;

, Ɛ > 0, 0 < Ɛ < k => k - Ɛ > 0

Если ряд сходится, тогда по теореме о сравнении => сходится

Если ряд расходится, тогда по теореме о сравнении => расходится и

20. Признак Даламбера.

Пусть - ряд с неотрицательными членами. Если, то

а) - ряд-сх-ся; б)- ряд- расходится;

в) - о сходимости ничего нельзя сказать.

3 Эталон: обобщенный гармонически ;

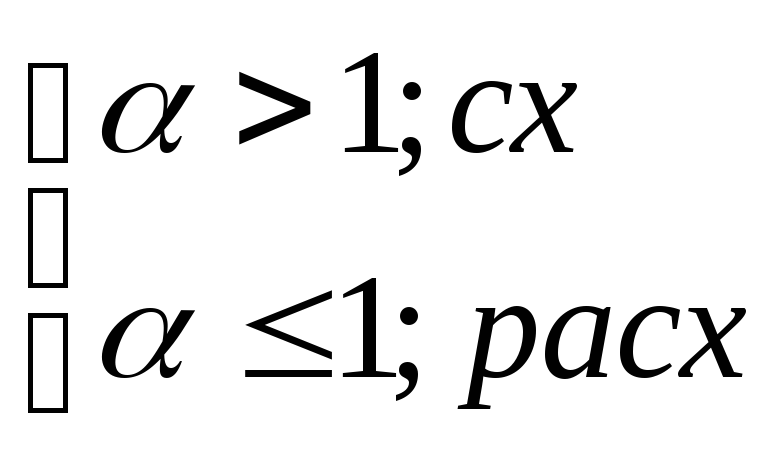
Доказательство:

по условию теоремы начиная сбудет выполняться условие;

а) Пусть начиная с:

;

члены исследуемого рода

меньше членов геометрической прогрессии

;Геометрическая прогрессия сх-ся.

б) ; пустьдля

ряд сходится.

21. Радикальный признак Коши.

Дан ряд ,если, то при

а) - ряд-сх-ся;

б) - ряд- расходится;

в) - о сходимости ничего нельзя сказать предполагается что предел

Доказательство:

_(*)

1. _cⁿ _{< 1, тогда найдём Ɛ > 0 | q = c + Ɛ < 1}

Тогда в (*) a_n < qⁿ v

По признаку сравнения из сходимости ряда, 0 <q < 1

• сходится и

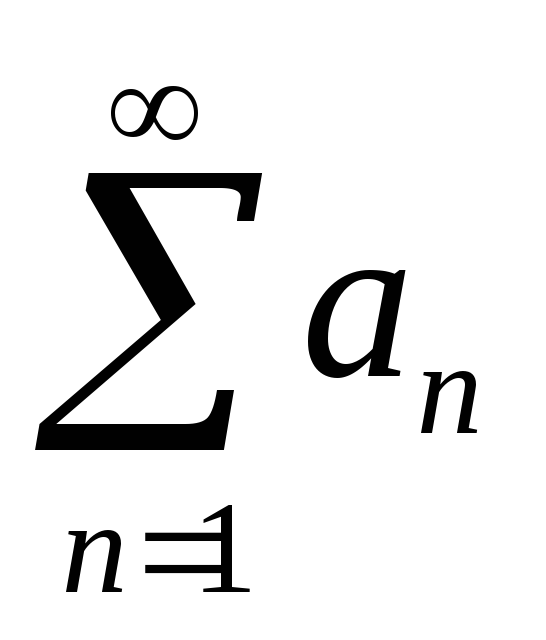
2. _cⁿ _{> 1, тогда найдём Ɛ > 0 | c – Ɛ = q > 1}

Тогда (*) из расходимости ряда, q > 1 => по теореме о сравнении, расходится и

22. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременных рядов.

Условную и абсолютную сходимости различают для рядов вида

Определение: Знакочередующийся ряд называют абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений членов данного ряда.

Если данный ряд по признаку Лейбница сходится, но ряд из абсолютных величин его членов расходится, то исходный ряд называют условно сходящимся.

Достаточным признаком сх-ти таких рядов является Признак Лейбница

Теорема Лейбница.

Если =0 (1) иu_n u_n+1>0, n=1,2,…,(2) то знакочередующийся ряд (3) сходится.

Доказательство:

Рассмотрим частичные суммы четного порядка ряда (3):

S_2k=.Их можно записать в видеS_2k=(u₁-u₂)+(u₃-u₄)+…+(u_2k-1-u_2k), k=1,2,…

В силу условия (2) выражения в круглых скобках неотрицательны и потому S_2kS_2(k+1), т.е. последовательность частичных сумм четного порядка ряда (3) монотонно возрастает.

Замечая, что частичные суммы S_2k можно записать также и в виде

S_2k=u₁-(u₂-u₃)-…-(u_2k-2-u_2k-1)-u_2k, k=1,2,… , и что выражения в круглых скобках в силу условия (2) неотрицательны, а u_2k>0, получаем, что S_2k<u­₁, т.е. последовательность {S_2k} ограничена сверху.

Из монотонного возрастания и ограниченности сверху последовательности {S_2k} следует, что она сходится.

Пусть =S (4). Покажем, что и частичные суммы нечетного порядка ряда (3) стремятся к тому же пределу. Действительно, S_2k+1=S_2k+u_2k+1, k=1,2…(5), и так как, согласно (1), , то в силу (4) и (5) имеем(6). Из (4) и (6) следует что.