14. Теорема о структуре общего решения лнду

ЛНДУ

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = f(x) (1) P_i – непрерывна на отрезке (a,b)

Теорема о структуре общего решения ЛНДУ

Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения

Док-во:

Для уравнения 2-го порядка ( но теорема применима для уравнений любого порядка)

n=2

(1’) y” + P₁(x) y’ + P₂(x) y = f(x)

Обозначим у*(х) – частное решение ЛНДУ

(х) – общее решение ЛОДУ

Показать, что

(2) у= у*+- общее решение ЛНДУ

Найдем:

Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)

у*”(x) +”(x) + P₁(x)[ у*(x)+’(x)] + P₂(x)[ у*(x)+(x)] =

= [у*”(x)+ P₁(x) у*’(x)+ P₂(x) у*(x)] + [”(x) + P₁(x) ’ (x)+ P₂(x)(x)] = f(x) + 0 = 0

= C₁y₁(x) + C₂y₂(x), y_1,y₂ – частное решение ЛОДУ y” + P₁y’ + P₂ = 0

C₁C₂ – подбираем так, чтобы они удовлетворяли начальным условиям

y(x₀)=y₀ , y’(x₀)=y₀’, для любых х₀(а,в), и любыхy₀ ,y₀’

C₁y₁(x₀) + C₂y₂(x₀) + у*(x₀) = y₀

C₁y’₁(x₀) + C₂y’₂(x₀) + у*(x₀) = y₀’

Линейная неоднородная система, определитель этой системы, определитель Вронского

W[y_1, y₂]≠0 =>система имеет единственное решение при любых ₀ , ’₀ ,y*_{0 ,}y*’₀ , это означает у= у*+- общее решение ЛНДУ

15. Теорема о суперпозиции решений (принцип сложения решений)

Если функция y_i(x) является решением ЛНДУ

(3) y⁽ⁿ⁾ + P₁y^(n-1) + … + P_ny = f_i(x) то функция = α₁y₁ + α₂y₂ + … + α_ny_n , то это функция является решением y⁽ⁿ⁾ + P₁y^(n-1) + … + P_ny = α₁ f₁(x) + α₂ f₂(x) + … + α_n f_n(x) (4)

Док-во: для n=2

y = α₁y₁ + α₂y₂

y’ = α₁y₁’ + α₂y₂’

y’’ = α₁y₁’’ + α₂y₂’’

Подставим y, y’, y”, в (4) , учитываем что y₁ y₂ решение соответственного уравнения (3)

α₁y₁” + α₂y₂” + P₁(x)[ α₁y₁’+ α₂y₂’] + P₂(x)[ α₁y₁+ α₂y₂] =

= [α₁y₁” + P₁(x)α₁y’₁ + P₂(x)α₁y₁] + [α₂y₂” + P₁(x)α₂y’₂ + P₂(x)α₂y₂] = α₁f₁(x) + α₂f₂(x)

16. Метод вариации произвольных постоянных – метод Лагранжа

Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.

ДУ 2-го порядка. Пусть y”+P₁(x)y’+P₂(x)y=f(x) (1) пусть y₁(x) и y₂(x) - ФСР ЛОДУ

y”+P₁(x)y’+P₂(x)y=0 (x)= C₁y₁(x)+C₂y₂(x) (2). Частное решение y*(x) в виде (14) считая при этом C₁ и C₂ не постоянными, а неизвестными функциями от x.

y*= C(x)y(x)+C(x)y(x), y*= C’(x)y(x)+C(x)y’(x)+C’(x)y(x)+ C(x)y’(x)

Пусть C(x) и C(x)C’(x)y(x)+ C’(x)y(x)=0 /справедливое равенство (3), тогда y* ’= C(x)y’(x)+ C(x)y’(x); y* ”= C(x)y’(x)+ C(x)y”(x)+ C’(x)y’(x)+ C(x)y”(x).

Подставим y*, y* ’, y* ” в (1): C(x)[ y”(x) + P(x)y’(x) + P(x) y(x)] + C(x)[ y”(x) + P(x)y’(x) + P(x) y(x)] + C’(x)y’(x)+ C’(x)y’(x)=f(x). Т.к. y(x), y(x) решения ОДУ, то выражения []=0C’(x)y’(x) + C’(x)y’(x)=0.

Объясним два условия и (3):

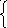C’₁(x)y₁(x)+ C’₂(x)y₂(x)=0

C’₁(x)y’₁(x)+ C’₂(x)y’₂(x)=f(x) (4)

Неопределённые функции C’₁(x) и C’₂(x).

Определитель этой системы: W[y₁, y₂]=0решая эту систему, мы получим C(x)=(x), C(x)=(x) проинтегрируем и получим решениеC₁(x) и C₂(x) найдены. Подставим в y*.

Для ЛНДУ n-го порядка ф-ии C_i(x) определяются из системы:

C’(x)y+ C’(x)y+…+ C’(x)y=0

C’(x)y’+ C’(x)y’+…+ C’(x)y’=0

……………………………………………

C’(x)y+ C’(x)y+…+ C’(x)y=0

C’(x)y+ C’(x)y+…+ C’(x)y=f(x)