5. Спектр колебаний с флуктуирующей частотой

Рассмотрим узкополосный процесс вида (5.7) с постоянной огибающей A₀:

.

(5.19)

Пусть величина , которую называютдевиацией мгновенной частоты, является стационарным случайным процессом, а начальная фаза₀, представляет собой случайную величину, распределенную равномерно на интервале [0, 2]. Выберем₀так, чтобыи запишем функцию автокорреляции величины(t):

.

Запишем случайный набег фазы на интервале [t,t+]

и вычислим его средний квадрат

(5.20)

Таким образом, средний квадрат набега фазы определяется спектральной плотностью интенсивности флуктуаций частоты.

Пусть теперь девиация мгновенной частоты (t), а значит – и случайный набег фазы_(t), распределены нормально. Поскольку <_(t)> = 0, а дисперсия определена выражением (5.20), функция плотности вероятности_(x) имеет вид

.

Рассмотрим произведение (t)(t+) и затем усредним его:

.

Второй косинус в этой сумме зависит от времени, а функция автокорреляции нашего стационарного процесса от времени зависеть не должна, поэтому его среднее должно дать ноль. Усреднение первого косинуса дает

.

Теперь можно записать выражение для односторонней спектральной плотности интенсивности, пользуясь выражениями (4.6):

.

Второй интеграл, содержащий быстроосциллирующий косинус можно отбросить, поскольку на суммарной частоте экспонента сильно затухает, и записать

.

(5.21)

Подставляя в это выражение значение D_() из формулы (5.20), получим окончательный результат. Однако, получить аналитические соотношения дляв общем случае не удается, поэтому мы рассмотрим два предельных случая, для чего введем интервал корреляции_процесса(t) так, чтобы. (проиллюстрировать это!)

1) Медленные и большие флуктуации частоты:. При таком условии для<<_разложим множитель (1 –cos()) в выражении (5.20) в ряд и получим:

Подставляя этот результат в (5.21), получим:

.

Экспонента выделяет в подынтегральном выражении времена , что и оправдывает разложение множителя (1 –cos()). Вычисляя интеграл, получим

–

гауссов спектр. Примером такого случая может служить доплеровское уширение спектральных линий.

2) Малые и быстрые флуктуации частоты:. В этом случае в выражении (5.20) существенны только те значения, которые находятся вблизи главного максимума функции {1 –cos()}/², то есть в диапазоне частот [0,…, 1/]. Поэтому еслии>>_, из (5.20) получим:

.

(5.22)

Теперь выражение (5.21) дает

.

Очевидно, здесь в интеграл вносят вклад времена < 1/C, что совмещается с нашим предположением>>_, если. Если функциядостаточно монотонно убывает с ростом частоты, можно положить, тогда предположение_<< 1/C, будет выполняться в силу исходного. В этом случае спектральная плотность интенсивности случайного процесса (5.20) примет вид

,

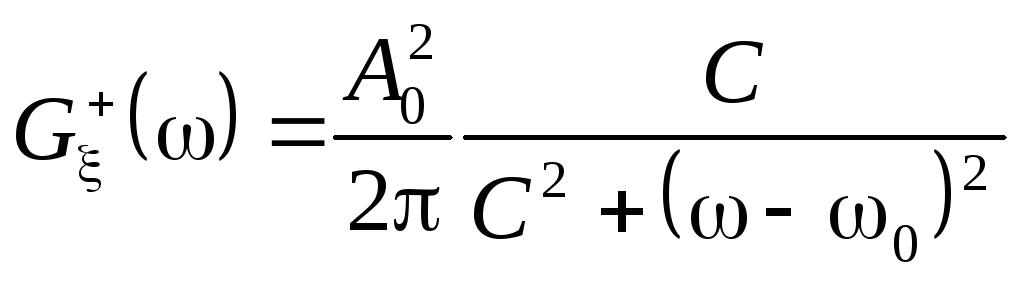соответствующий лоренцевой форме. Ее, в частности, имеют спектральные линии, уширенные вследствие столкновений.

6. Спектральное оценивание

На практике при измерении статистических характеристик физических величин возможно усреднение только по конечному числу реализаций, либо на ограниченном временном интервале [0, T]. Полученные таким образом характеристики называютсяоценкамии сами являются случайными величинами, имеющими некоторые среднее и дисперсию. Рассмотрим автокорреляционную функциюB_T() и спектральную плотность интенсивностиG_T() некоторого эргодического случайного процесса, усредняемого на интервале [0,T].

Оценка G_T() называется несмещенной, если

(5.23)

и состоятельной, если

.

(5.24)

Аналогичные определения существуют и для оценки автокорреляционной функции B_T().

Рассмотрим оценивание спектральной плотности интенсивности методом фильтрации, когда в течение времени Tусредняется квадрат напряжения на выходе идеального узкополосного фильтра, на вход которого подан случайный процесс(t). Пусть частотная характеристика фильтра имеет вид

Если полоса фильтра 2достаточно мала, в ее пределах можно считатьG(j) =G(j₀) =const. Тогда с учетом выражений (4.5), (5.1) и (5.3) получим:

.

Заметим, что эргодичность исследуемого процесса (t) вообще говоря не означает эргодичности произведения(t–₁)^*(t–₂), однако множество реальных процессов удовлетворяют условию

.

(5.25)

Такие процессы называются корреляционно-эргодическими. Доказано, что нормальный эргодический процесс является и корреляционно-эргодическим, а в силу теоремы о нормализации процесс на выходе нашего фильтра является нормальным. Поэтому для него на основе (4.4) мы можем продолжить вычисления:

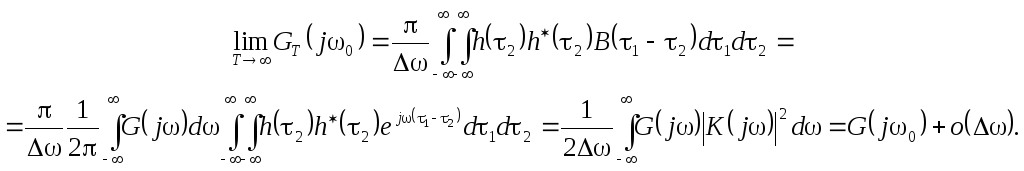
Таким образом, при конечной ширине полосы пропускания фильтра оценкаG_T(j) оказывается смещенной. Однако ее можно считать асимптотически несмещенной поскольку она стремится кG(j) при0. Можно показать (без вывода), что при достаточно малых значенияхдисперсия оценкиG_T(j) определяется приближенным выражением

,

что в соответствии с определением (5.23) позволяет говорить о ее состоятельности при T.

Обсудим возможные методы оценивания автокорреляционной функции и спектральной плотности интенсивности. На практике обычно приходится иметь дело с одной реализацией случайного процесса, поэтому вычисление автокорреляционной функции путем усреднения по ансамблю невозможно. При таких обстоятельствах единственно возможной операцией является ее расчет на конечном временном интервале в предположении, что наблюдаемый процесс является эргодическим. Если в распоряжении наблюдателя имеется реализация x(t) процесса(t) на интервале [0,T], за оценку автокорреляционной функции обычно принимают следующую величину:

.

(5.26)

Ясно, что эта функция сама является случайной величиной. Время усреднения в этом выражении (T–) уменьшается по мере увеличения сдвига, поскольку имеющаяся реализация ограничена интервалом наблюдения [0,T].

На практике математическое выражение для x(t) неизвестно, поэтому приходится оперировать выборкой отсчетов реализации, взятых в моменты времениnt(n= 0, .. ,N – 1) а вместо интеграла в выражении (5.25) использовать сумму:

,

(5.27)

причем B_T[–m] =B_T[m] . Оценка (5.27) является несмещенной оценкой автокорреляционной последовательности, поскольку ее усреднение дает истинное значениеB[m] =B(mt):

.

Можно показать, что для гауссовых случайных процессов при малых m<<Nдисперсия этой оценки составляет

.

Поскольку при больших временных сдвигах усреднение ведется по небольшому числу отсчетов, дисперсия несмещенной оценки АКП растет с увеличением m. С другой стороны видно, чтоD{B_T[m]}приN, что означает состоятельность оценки (5.27).

Альтернативной и применяемой чаще является следующая оценка автокорреляционной последовательности:

.

(5.28)

Она легко выражается через несмещенную оценку:

,

откуда следует

.

Однако при Nсмещенная оценка (5.28) сходится к истинной последовательностиB[m] и поэтому является асимптотически несмещенной. Для гауссовых случайных процессов при малыхm<<Nдисперсия этой оценки может оцениваться выражением

,

которое позволяет сделать вывод о состоятельности смещенной оценки .

На основе рассчитанных по формулам (5.27) или (5.28) оценки автокорреляционной последовательности можно получить так называемые коррелограммныеоценки спектральной плотности интенсивности, которые определяются выражениями

.

(5.29)

Вычислим среднее оценки спектральной плотности интенсивности, полученной по несмещенной оценке автокорреляционной последовательности:

.

Здесь W() – спектр прямоугольногокорреляционного окна, которое определяется выражением

Таким образом, оценка G_T(j) смещена, хотя и построена на основе несмещенной оценки АКП. Очевидно, смещена и вторая оценка:

,

где W₁() – спектр треугольного корреляционного окна вида

Для уменьшения эффекта просачивания боковых лепестков спектра при вычислении оценки спектра можно использовать корреляционные окна, однако необходимо помнить, что спектр используемого окна не должен иметь отрицательных значений, в противном случае появятся отрицательные значения у найденной спектральной плотности интенсивности, что противоречит ее физической сути. Таким образом, прямоугольное корреляционное окно не следует применять при реализации коррелограммного метода. В общем виде коррелограммная оценка спектральной плотности интенсивности может быть записана в виде:

,

где w[m] – какое-либо корреляционное окно, аB_T[m] – одна из оценок автокорреляционной последовательности (5.27) или (5.28). При выборе последней следует знать, что хотя обе они сохраняют мощность исследуемого процесса, несмещенная оценка может дать нереальные значения, когдаB_T[m] >B_T[0] (примером может служить последовательность {1, 1.1, 1}). Обычно оценка спектра вычисляется на сетке изKэквидистантных частот с шагом:

,

(5.30)

причем для лучшей детализации спектра обычно берут K >>M.

Периодограммнаяоценка спектральной плотности интенсивности основана на получении спектров реализаций случайного процесса с их последующим усреднением, как это следует из выражения (4.7). Если в распоряжении исследователя имеетсяNотсчетов реализации случайного процесса, оценка выборочного спектра (периодограмма) может быть записана в виде

,

(5.31)

однако такая оценка является статистически несостоятельной. Для получения статистически значимой оценки необходимо применить операцию усреднения периодограмм по ансамблю. Существуют три основных способа это сделать. При усреднении выборочного спектра по соседним частотам получим периодограмму Даньелла:

.

Периодограмма Бартлетаоснована на создании и последующем усреднении псевдоансамбля периодограмм вида (5.31), каждая из которых вычислена по одному из неперекрывающихся сегментов данных, содержащемуLотсчетов. Обобщением периодограммы Бартлета являетсяпериодограмма Уэлча, в которой предусмотрено частичное перекрытие сегментов. При использовании периодограммы Уэлча на основе исходной реализацииx[n] (n= 0,…,N– 1) формируются сегменты данных в виде

,

где R– количество перекрывающихся отсчетов. Оценка выборочного спектра, рассчитанная по сегменту с номеромqравна

,

а полный вид периодограммы Уэлча записывается как среднее значение периодограмм сегментов:

.

При необходимости каждый сегмент перед вычислением выборочного спектра может взвешиваться какой-либо оконной последовательностью.