7. Марковские процессы 70

7. Марковские процессы

Эти процессы являются частным случаем случайных процессов, однако многие физические явления хорошо описываются с помощью аппарата марковских процессов.

1. Процессы без последействия

Рассмотрим случайный процесс (t), все конечномерные распределения которого известны. В соответствии с выражением (3.4), его n-мерную функцию распределения _n можно выразить через n–1-мерную _n–1 и одномерную условную :

.

(7.1)

Произведение (t_n, x_n| t₁, x₁,…, t_n–1, x_n–1)dx_n дает условную вероятность того, что x_n < (t_n) < x_n + dx_n, при условии, что (t_i) = x_i. Таким образом, условная вероятность для момента времени t_n определяется множеством предыдущих состояний в моменты времени t₁, …, t_n–1. Говорят, что случайный процесс испытывает вероятностное последействие со стороны своих прошлых значений. Частным случаем является процесс без последействия, когда

(t_n, x_n| t₁, x₁,…, t_n–1, x_n–1) = (t_n, x_n| t_n–1, x_n–1),

а выражение (7.1) принимает вид

.

(7.2)

Случайные процессы, функции плотности вероятности которых удовлетворяют соотношению (7.2), называют марковскими процессами первого порядка. Применяя выражение (7.2) последовательно n раз, получим

.

(7.3)

Таким образом, для полного задания функции _n марковского процесса необходимо знать только две функции плотности вероятности – _n(t₁, x₁) и (t_n, x_n| t_n–1, x_n–1). Условная функция распределения (t_n, x_n| t_n–1, x_n–1) называется вероятностью перехода из состояния t_n–1, x_n–1 в состояние t_n, x_n.

Для стационарного марковского процесса на основе выражения (3.2) можно записать

,

поэтому в силу условия согласования (3.1) получим

.

(7.4)

Если в качестве случайного процесса рассматривается случайная последовательность x_n = x(t_n), то для нее марковость означает, что существует вероятность перехода от любого x_i при l-м испытании к любому x_k при n-м испытании:

.

(7.5)

Если при этом случайная величина _n принимает конечное множество возможных значений, то последовательность называют простой цепью Маркова. Ясно, что для стационарной марковской последовательности вероятность перехода вида (7.5) зависит только от сдвига индекса m = n – l, то есть от числа шагов между состояниями:

.

Если при дискретном времени t_n значения x случайной величины _n = (t_n) образуют непрерывное множество, то марковость процесса означает, что существуют вероятности переходов

,

а условие стационарности имеет вид:

.

2. Уравнение Смолуховского

В этом параграфе мы рассмотрим связь между вероятностями перехода для трех моментов времени t₁ < t₂ < t₃. Используя условие согласования (3.2) и определение марковского процесса (7.2) для момента времени t₃ запишем:

.

Если известно, что (t₁) = x₁, то

.

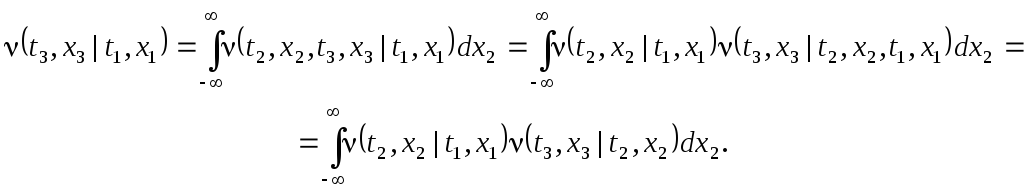Мы получили уравнение Смолуховского:

.

(7.6)

Для дискретного множества значений x уравнение (7.6) принимает вид

.

(7.7)

Для случайной последовательности момент времени t_n надо заменить на номер шага n:

.

Для стационарного случайного процесса уравнение Смолуховского (7.6) несколько упрощается:

.