4. Основы корреляционной теории случайных процессов 42

4. Основы корреляционной теории случайных процессов

Как уже упоминалось в п. 3.2, одной из важнейших характеристик случайного процесса является его корреляционная функция. В данном разделе для изучения свойств случайных процессов мы будем пользоваться именно корреляционными функциями, то есть смешанными моментами второго порядка.

1. Функция автокорреляции

Рассмотрим комплексную случайную функцию вида (t) = (t) + j(t), которую можно рассматривать как двумерную случайную функцию, либо как комбинацию из двух действительных случайных функций. Как уже упоминалось в п.. 3.2, функцией автокорреляции называется смешанный момент второго порядка вида

.

(4.1)

Здесь введены обозначения _i = (t_i) и _i =  (t_i). Естественно, B(t, t) является действительной положительной величиной:

.

(4.2)

Из определения функции автокорреляции комплексного процесса (4.1) следует также ее эрмитовость:

,

что для процессов, стационарных в широком смысле, дает . Из выражения (4.2) следует, что дисперсия функции (t) может быть вычислена как

.

Ограничим класс рассматриваемых нами случайных функций непрерывными в среднеквадратичном смысле функциями второго порядка, то есть имеющими ограниченный и непрерывный в любой момент времени средний квадрат модуля. Представим функцию автокорреляции в показательной форме B(t₁,t₂) = |B(t₁,t₂)|exp{(t₁,t₂)} и рассмотрим при произвольном a величину

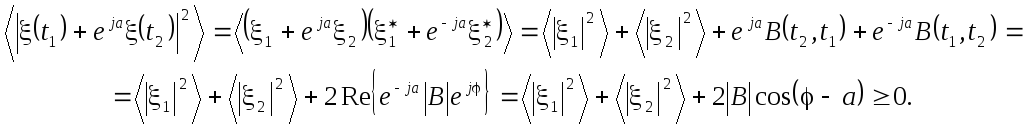
Поскольку среднее от квадрата модуля любой величины неотрицательно, а |cos( – a)|  1,

получаем

,

то есть функция автокорреляции ограничена по модулю. Очевидно, для стационарного случайного процесса |B()|  <|(t)|²> = B(0). Кроме того, функция автокорреляции непрерывной в среднеквадратичном смысли случайной функции равномерно непрерывна на плоскости (t₁, t₂).

Для того, чтобы производная случайной функции (t) существовала и была случайной функцией второго порядка, непрерывной в среднеквадратичном смысле, необходимо и достаточно, чтобы существовала непрерывная в любые моменты времени смешанная производная . Тогда

.

Для стационарного случайного процесса

.

Аналогично можно показать, что

, ,

а для стационарных процессов

.

2. Спектральные характеристики случайных процессов

Рассмотрим стационарный в широком смысле непрерывный в среднеквадратичном смысле случайный процесс второго порядка (t). Как было показано в предыдущем параграфе, функция автокорреляции B() такого процесса ограничена и непрерывна для любого , а это означает, что существует ее преобразование Фурье:

.

(4.3)

Функция G(j) называется спектральной плотностью интенсивности случайного процесса. Для электрических сигналов эта функция имеет смысл спектральной плотности мощности. Соответственно, существует и обратное преобразование

.

(4.4)

Соотношение (4.4) носит название теоремы Винера-Хинчина.

Положив в выражении (4.4)  = 0 и учитывая соотношение (4.2), получим:

.

(4.5)

Если стационарный случайный процесс (t) – вещественный, то его функция автокорреляции B() также вещественная и четная; тогда и спектральная плотность интенсивности G(j) тоже будет вещественной и четной функцией частоты. Поэтому имеет смысл изменить пределы интегрирования в теореме Винера-Хинчина и ввести другую спектральную функцию:

.

Здесь

и G⁺(f) = 2G⁺(2f). Выражения для спектральных интенсивностей G⁺(f) и G⁺() легко получить из формулы (4.3):

.

(4.6)

Если все реализации случайного процесса (t) – финитные функции, для любой из этих реализаций s(t) можно построить ее спектр S(j):

,

который, очевидно, будет являться случайной функцией частоты. Если случайный процесс стационарен, то, используя спектр реализации процесса и теорему Винера-Хинчина (4.4), мы можем записать:

Полученное равенство может выполняться только в случае, когда

.

(4.7)

Именно это соотношение часто принимают за определение спектральной интенсивности случайного процесса; в этом случае выражение (4.4) действительно имеет смысл теоремы.

Рассмотрим случайный процесс с нулевым средним ₁ (t) = (t) – <(t)>. Легко показать, что для его спектральной плотности интенсивности справедливо

.

Введем среднюю частоту , среднее время корреляции , ширину полосы  и интервал корреляции , которые определяются следующими выражениями

, ,

, ,

если существуют соответствующие интегралы. Из теории интегралов Фурье известно, что для произведения квадратов ширины полосы и интервала корреляции справедливо соотношение неопределенностей:

.

(4.8)

В квантовой механике энергия , поэтому из выражения (4.8) следует

–

классическое соотношение неопределенности Гайзенберга. Доказано, что равенство в выражении (4.8) реализуется только для гауссовых функции корреляции и спектральной плотности интенсивности:

, .

(4.9)

В качестве примера найдем спектральную плотность интенсивности пуассоновского импульсного процесса вида (2.3), рассмотрев сначала процесс с нулевым срелним (t) = (t) – <(t)>. По аналогии с выводом соотношения (2.10) выразим B() через условные моменты и, учитывая, что < (t)> = 0, получим:

.

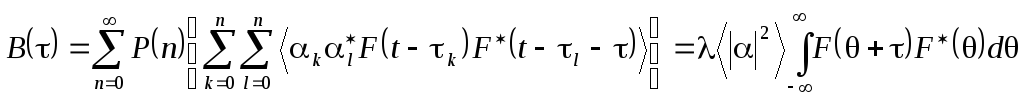Применив теорему о спектре свертки, запишем спектральную плотность интенсивности:

,

где

–

спектр импульса F(t). Таким образом, форма спектральной плотности интенсивности пуассоновского импульсного процесса полностью определяется формой спектра импульсов F(t), а их средняя частота следования и амплитуда влияют только на общий уровень шума.

В задаче о дробовом эффекте мы полагали импульс F(t) прямоугольным c единичной высотой и длительностью ₀. Соответствующий такому импульсу спектр равен

;

соответственно, спектральная плотность интенсивности дробового шума с учетом выражений и равна

.

(4.10)

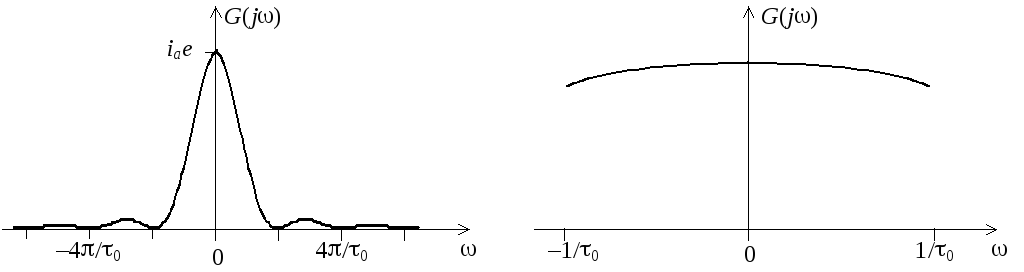
Вид этой функции показан на рис. 4.1. Видно, что при ₀ << 1 ее можно считать практически постоянной и равной G₀ = i_аe.

Случайный процесс, спектральная плотность интенсивности которого постоянна G(j) = G₀, называется белым шумом. Ясно, что такого шума в природе быть не может, поскольку в соответствии с выражением (4.5) для него . Однако эта абстрактная модель может применяться в случаях, когда спектральная плотность интенсивности реального процесса постоянна в некотором частотном диапазоне. Рассмотрим случайный процесс, функция автокорреляции которого локализована на интервале –₀ <  < ₀, то есть B() = 0 при || > ₀. Тогда на частотах  << 1/₀ спектральная плотность интенсивности равна

Рис. 4.1. Спектральная плотность интенсивности дробового шума

,

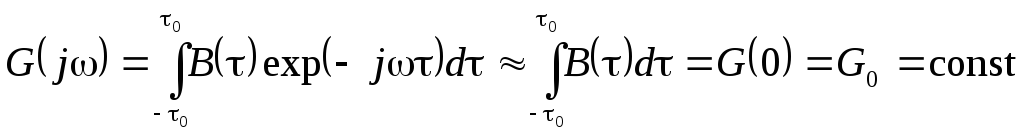то есть шум можно считать белым. В пределе при ₀  0 так, чтобы интеграл от функции автокорреляции оставался постоянным, получим белый шум во всем частотном диапазоне G(j) = G₀, которому соответствует автокорреляционная функция

.

(4.11)

По этой причине белый шум часто называют дельта-коррелированным процессом.
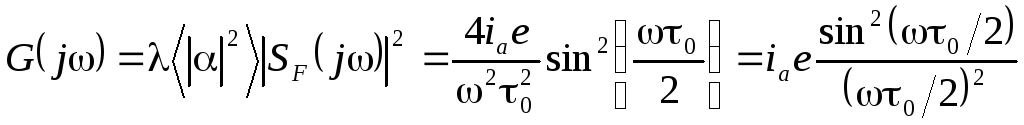