Downloads / А.В. Никитин - Статистическая радиофизика / srf_2

2. Случайный импульсный процесс 26

2. Случайный импульсный процесс

При решении основных задач статистической радиофизики приходится оперировать понятием случайной функции, которое мы дадим в п. 3. Однако случайный импульсный процесс является классическим примером задачи, при решении которой достаточно серьезные результаты можно получить, не вводя понятия случайной функции, а пользуясь только понятием функции случайной величины.

1. Функция случайной величины

Под функцией случайной величины (ФСВ) мы будем понимать детерминированную функцию, зависящую от какого-либо параметра (от времени, координаты и т. д.) и конечного числа случайных величин. Например

–

функция случайной величины, зависящая от времени.

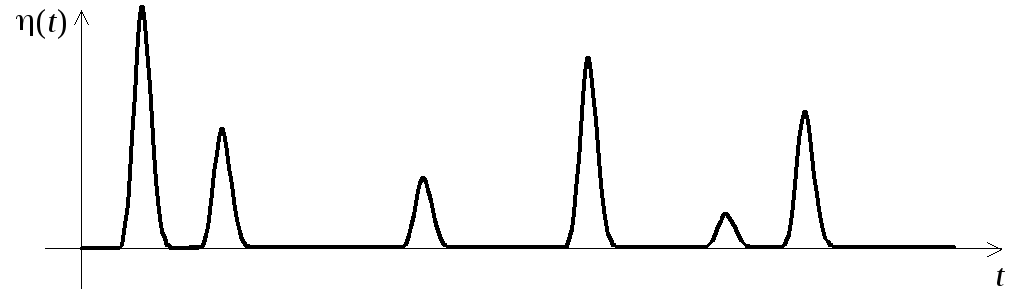
Рис. 2.1. Случайная импульсная последовательность

Классическим примером ФСВ является последовательность возникающих в случайные моменты времени импульсов одинаковой формы со случайной высотой (рис. 2.1), которая может быть описана в виде

.

Сформулируем общую задачу, которая ставится при описании процесса с помощью ФСВ. Пусть задано совместное распределение вероятностей _N(x₁,…,x_N) совокупности случайных величин ₁,…, _N и задана совокупность M однозначных непрерывных функций N переменных вида

Необходимо найти совместное распределение вероятностей W_N(y₁,…,y_N) случайных величин ₁,…, _M. В одномерном случае задача сводится к нахождению распределения W₁(y) случайной величины  = f(), если известно распределение ₁(x).

Рассмотрим одномерную задачу и предположим, что функция f(x) дифференцируема и существует обратная функция x = g(y), то есть связь величин  и  взаимно однозначна. Тогда, очевидно, при df/dx > 0 вероятность P{  y} = P{  x = g(y)}, а при df/dx < 0 вероятность P{  y} = P{  x = g(y)}. Используя определение функции плотности вероятности (1.6), получим:

Объединяя эти равенства, получим

.

(2.1)

В качестве примера рассмотрим линейную зависимость  = f() = a + b, где в качестве случайного выступает гауссов процесс с нулевым средним и дисперсией ² вида (1.12). Согласно (2.1) получим:

.

Рассмотрим случай, когда функция y = f(x) такова, что обратная ей функция x = g(y) неоднозначна, то есть одному значению y соответствует несколько значений g(y) – x₁, x₂ и т. д.. В этом случае событию y    y + dy соответствует одно из взаимоисключающих событий: x₁    x₁ + dx₁, x₂    x₂ + dx₂ и т. д., а вместо выражения (2.1) можно записать

.

(2.2)

Примером такого случая может служить квадратичное преобразование  = ², того же гауссова процесса с нулевым средним. Функция плотности вероятности процесса  будет иметь вид:

.

Еще один вариант реализуется, когда из одной случайной величины получаются две – ₁ = f₁() и ₂ = f₂(), причем существует обратная функция  = g₁(₁). Тогда ₂ = f₂(g₁(₁)) = F(₁), а условное распределение имеет вид

,

что с учетом (1.20) дает возможность записать

.

Аналогично, если известна двумерная функция плотности вероятности (x₁, x₂) и зависимости ₁ = f₁(₁, ₂) и ₂ = f₂(₁, ₂) при наличии обратных функций (не обязательно однозначных) ₁ = g₁(₁, ₂) и ₂ = g₂(₁, ₂), двумерная функция W₂(y₁, y₂) может быть записана в виде

.

(2.3)

Здесь индекс k определяет номер неоднозначности обратных функций, а величина

–

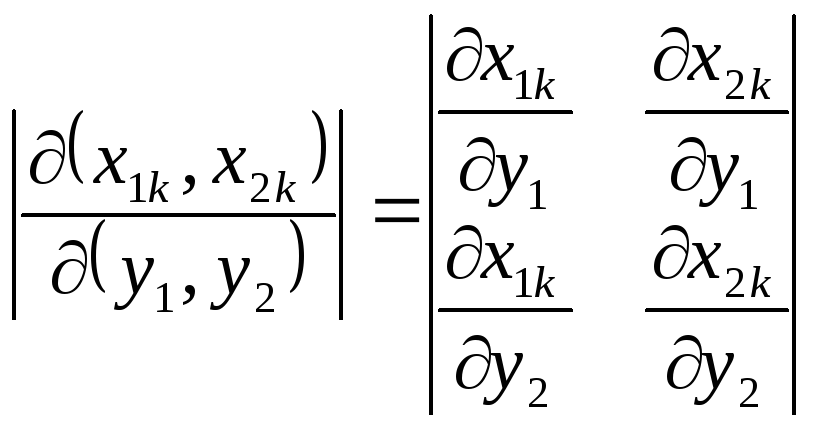якобиан преобразования. Естественно, при однозначных преобразованиях в этом выражении будет только один член.

Используя предыдущее соотношение и выражения (1.17), нетрудно найти распределение одной случайной величины, являющейся функцией двух других, то есть  = ₂ = f₂(₁, ₂), положив ₁ = ₁. Тогда

.

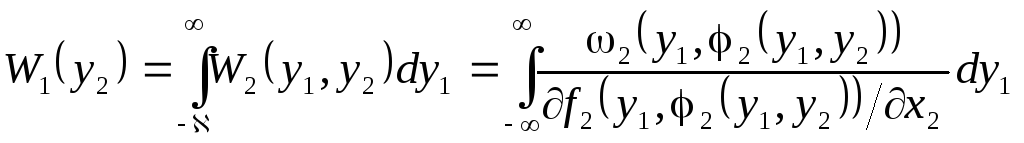2. Пуассоновский импульсный процесс

Рассмотрим импульсный процесс вида

,

(2.4)

являющийся функцией случайных величин _i,  _i и  и сделаем ряд предположений:

1. Предположим, что функция F(t) затухает достаточно быстро, то есть .

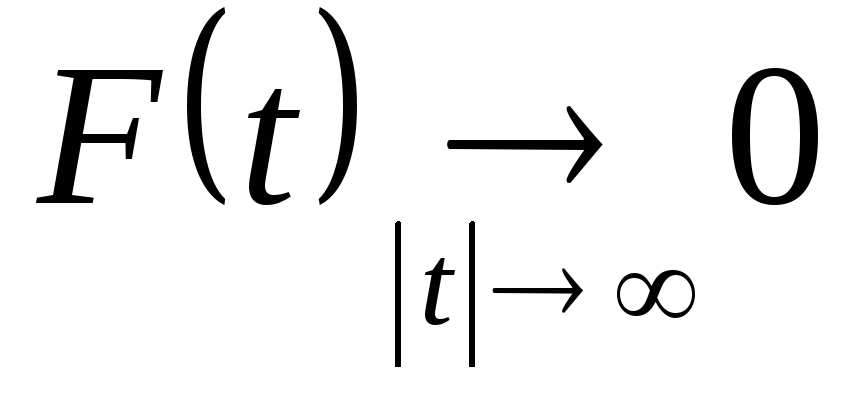2. Будем считать, что величины _i и _i статистически независимы между собой и их распределения не зависят от номера i. Фактически это означает, что 2-мерная функция распределения этих величин распадается на множители:

.

3. Пусть вероятность появления импульса в интервале [t, t + dt] не зависит от времени t и количества предшествующих импульсов и пропорциональна длине интервала dt:

dP = dt,  = const.

(2.5)

Заметим, что последнее предположение в принципе может быть справедливо только на малых интервалах dt, поскольку dP  1.

Вычислим вероятность появления n импульсов на временном интервале [0, t] P(n, t). Эту вероятность можно представить как сумму вероятностей двух несовместных событий:

1. появление n импульсов на интервале [0, t – dt] и ни одного на интервале [t – dt, t];

2. появление n – 1 импульса на интервале [0, t – dt] и одного на интервале [t – dt, t].

Остальными вариантами можно пренебречь, учитывая соотношение (2.5) и малость интервала [t – dt, t]. Таким образом

P(n, t) = P(n, t – dt)(1 – dt) + P(n – 1, t – dt)dt.

Полагая

,

при dt  0 получим:

или

.

Введем производящую функцию вида

и преобразуем полученное выражение, домножив его на sⁿ и суммируя по всем n:

.

Учитывая, что

,

получим уравнение для производящей функции:

.

Решение этого уравнения имеет вид

.

Поскольку P(0, 0) = 1 и P(n  1, 0) = 0, получаем G(s, 0) = 1, поэтому

.

Таким образом, мы показали, что распределение вероятностей совпадает с распределением Пуассона (1.10)

,

(2.6)

причем величина t = <n>. Кстати, это означает, что среднее число импульсов, появившихся на интервале [0, t] пропорционально длительности этого интервала.

Поскольку вероятность того, что на интервале [0, t] не появилось ни одного импульса, равна P(0, t) = e^–t, вероятность того, что интервал между двумя соседними импульсами  лежит в диапазоне [t, t + dt] можно найти как произведение вероятностей двух независимых событий – того, что за время t ни одного импульса не появилось и того, что на интервале [t, t + dt] появился один импульс:

.

Поскольку по определению P{t    t + dt} = (t)dt, легко записать вид функции плотности вероятности:

.

Теперь можно вычислить средний интервал между импульсами:

.

Таким образом, параметр распределения  имеет смысл средней частоты следования импульсов.

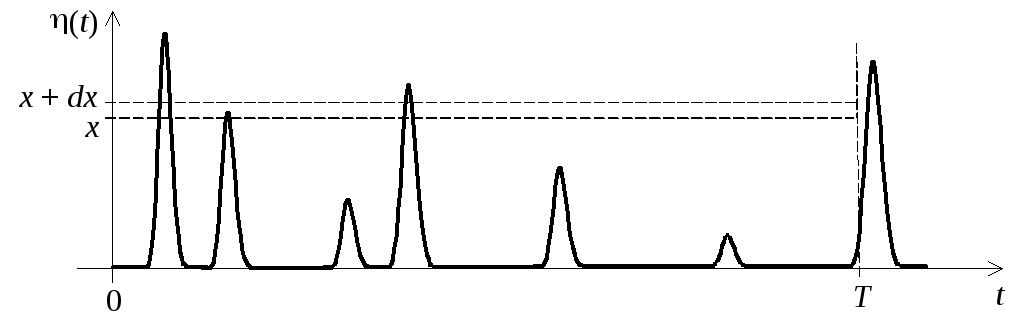
Выберем интервал наблюдения 0  t  T много большим как величины 1/, так и длительности одного импульса (то есть F(T) = 0). Тогда импульсы, появившиеся за пределами данного интервала, не будут вносить значительный вклад в функцию (t) и можно пренебречь краевыми эффектами, то есть влиянием тех импульсов, которые попадают в интервал частично. Найдем распределение (x) случайной величины (t) вида (2.6), то есть вероятность события A, заключающегося в том, что x  (t)  x + dx:

.

Очевидно, событие A (рис. 2.2) может реализоваться в результате появления за интервал наблюдения любого количества импульсов, поэтому используя формулу полной вероятности (1.4), мы можем записать

.

(2.7)

Рис. 2.2. Распределение случайной величины (t)

Здесь (x|n) – условная функция плотности вероятности величины (t) при условии, что за время T появилось n импульсов. Следовательно, моменты случайной величины (t) равны

,

(2.8)

где m_k(|n) – условные моменты величины (t) при условии появления n импульсов за интервал [0, T]. Вычислим первый условный момент, основываясь на определении (t) (2.4) и на предположении 2 о независимости случайных амплитуд _i и моментов появления _i:

.

Здесь

–

среднее значение _i, не зависящее от i.

Теперь рассмотрим среднее <F(t – t_i)>; для его определения необходимо задать функцию плотности вероятности _(t_i). Будем считать, что момент появления i-го импульса распределен равномерно на интервале [0, T], то есть _(t_i) = 1/T. Тогда

.

(2.9)

Здесь мы воспользовались локализованностью функции F(t). Подставляя полученное выражение (2.9) в формулу (2.8), запишем

.

Учитывая, что входящая в это выражение вероятность P(n) определяется распределением Пуассона (2.6) при t = T, то есть P(n) = P(n, T), получим

.

(2.10)

Совершенно аналогично найдем второй условный момент

.

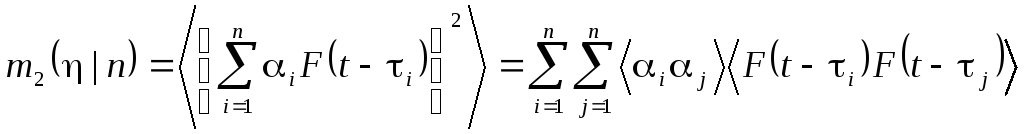Поскольку согласно нашим предположениям величины _i и _I независимы, получим:

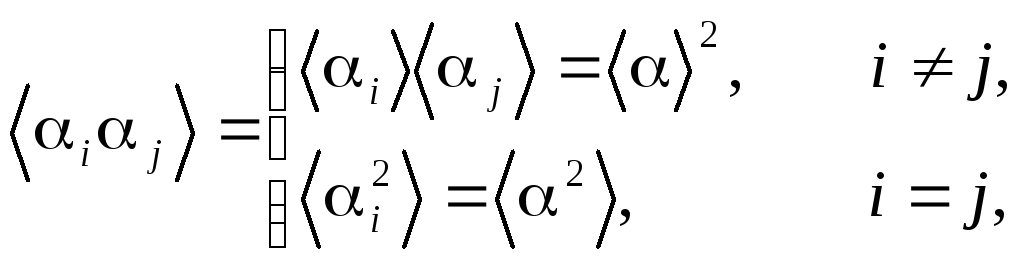
Таким образом, второй условный момент равен

.

Подставляя это выражение в формулу (2.8) с k = 2, получим

.

Учитывая, что для распределения Пуассона <n²> = <n>² + <n>, применяя соотношение (2.10), а также учитывая, что средняя частота следования импульсов  = <n>/T, запишем

.

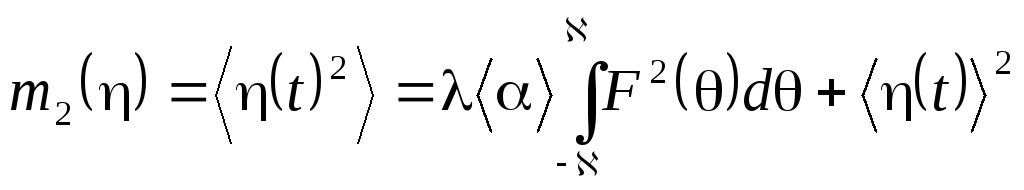Таким образом, дисперсия процесса определяется выражением

.

(2.11)

В частном случае, если импульсы имеют одинаковую высоту, то есть _i = a, на основе (2.10) и (2.11) получаем

.

(2.12)

Эта пара соотношений называется теоремой Кэмпбелла.

Рис. 2.3. Электронная лампа и ее анодный ток

На основе полученных результатов рассмотрим конкретный физический процесс – дробовой шум в электронной лампе. За счет термоэлектронной эмиссии электроны вылетают из нагретого катода независимо друг от друга и под действием электрического поля летят к аноду. Каждый пришедший к аноду электрон порождает в цепи импульс анодного тока, который мы обозначим F(t). Будем считать импульс F(t) прямоугольным c единичной высотой и длительностью ₀ (время пролета электрона через лампу). Полагая, что вероятность вылета электрона из катода за малое время dt пропорциональна этому времени, то есть dP = dt, получим пуассоновский импульсный процесс вида (2.4), где _i = I₀ = e/₀ (рис. 2.3):

.

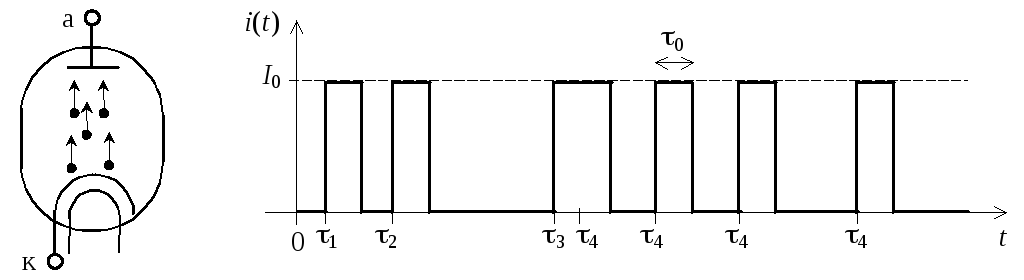
Учитывая, что

,

на основе теоремы Кэмпбелла (2.12) запишем

.

(2.13)

Однако любой амперметр регистрирует ток, усредненный на некотором временном интервале T >> ₀. Выполним усреднение, разбив интервал T на участки длительностью ₀ и суммируя значения i(t), взятые в точках t = k₀. Пусть K – количество участков ₀, полностью укладывающихся в интервале [0, T], тогда усредненный ток i_T(t) может быть записан в виде

.

Как видно из полученного выражения . Соответственно, дисперсия процесса равна

.

(2.14)

Мы получили известную формулу дробового эффекта.

Выясним, когда распределение величины (t) вида (2.4) близко к нормальному, для чего найдем характеристическую функцию процесса и семиинварианты. В п. 1.5 мы показали, что у нормального распределения все семиинварианты, начиная с третьего, равны нулю. Поскольку в рамках наших предположений о процессе все слагаемые в сумме (2.4) статистически независимы, условная характеристическая функция величины (t) при условии, что на интервале [0, T] появилось n импульсов, равна произведению характеристических функций слагаемых:

.

(2.15)

Здесь мы по-прежнему считаем, что момент появления каждого импульса распределен равномерно на интервале [0, T], то есть _(t) = 1/T.

Взяв преобразование Фурье от выражения (2.7), получим:

.

Подставляя сюда условную характеристическую функцию (2.15), вычислим _(u):

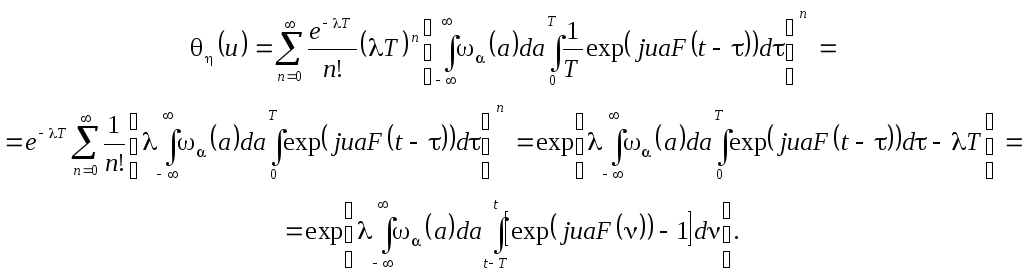
Пользуясь опять локализованностью функции F() и устремляя T  , получим:

Теперь можно вычислить семиинварианты, взяв ln{_(u)}:

.

Таким образом, семиинварианты характеристической функции определяются выражением

.

Теперь можно найти условия, при которых все _m, начиная с m = 3, малы – в этом случае распределение величины (t) вида (2.4) будет близко к нормальному. Запишем отношение модулей

.

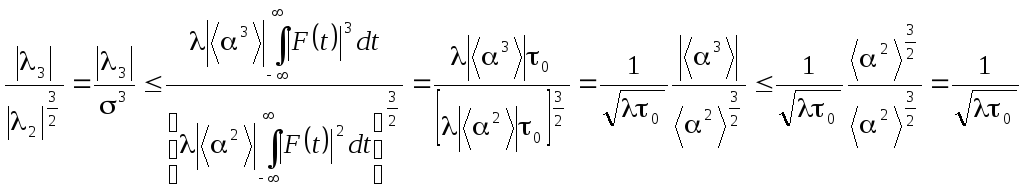Таким образом, при ₀ >> 1 |₃| << ³ и все семиинварианты, начиная с третьего, малы, а распределение величины (t) близко к нормальному вида (1.12). При этом среднее и дисперсия (t) определяются выражениями (2.10) и (2.11). Поскольку величина  является средней частотой следования импульсов, а ₀ – их длительностью, полученное условие означает, что импульсы густо перекрываются.
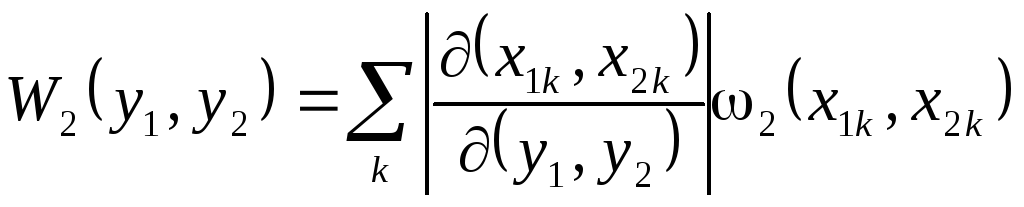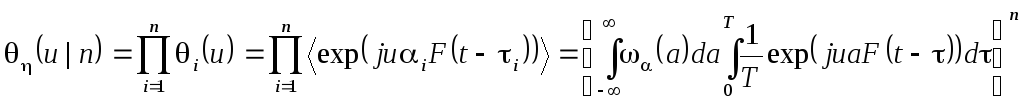