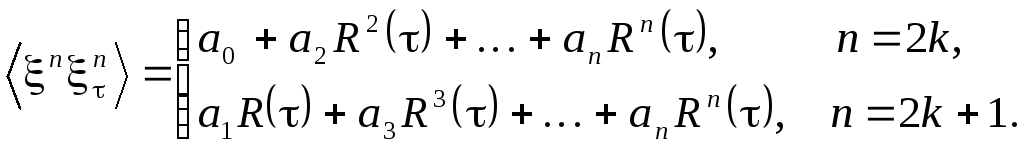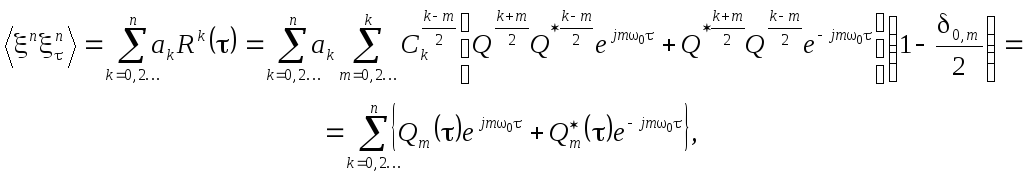6. Нелинейные преобразования случайных процессов 62

6. Нелинейные преобразования случайных процессов

В данном разделе мы рассмотрим спектральные и корреляционные характеристики процесса на выходе умножителя частоты, который является одним из примеров нелинейной безинерциальной системы.

1. Нелинейное безинерциальное преобразование

Рассмотрим безинерциальную систему, связь между процессами на входе и выходе которой дается чисто алгебраическим выражением вида

.

(6.1)

Далеко не все реальные нелинейные системы можно считать безинерциальными, однока в большинстве случаев их можно представить в виде последовательного соединения нелинейного безинерциального звена, описываемого выражением (6.1), и линейного фильтра с частотной характеристикой K(j).

Рассмотрим прохождение узкополосного случайного процесса вида (5.7) или (5.9)

(6.2)

через генератор гармоник (или умножитель частоты), нелинейное звено которого работает в соответствии с выражением

,

(6.3)

а линейная часть представляет собой полосовой фильтр, настроенный на частоту m₀ и имеющий полосу пропускания  << ₀, то есть выделяющий из сигнала только гармонику с номером m. Подставляя (6.2) в (6.3), получим:

.

(6.4)

Видно, что при четном n генерируются только четные гармоники, а при нечетном n – только нечетные. Гармоника с номером m описывается выражением

,

Средняя интенсивность этого процесса равна

,

(6.5)

где

.

На основе полученного выражения можно сделать вывод, что относительное распределение интенсивности процесса (t) по гармоникам (то есть – его спектр) уменьшается с ростом m, а его форма не зависит от характеристик входного процесса (6.2). Величина же КПД генерации гармоники существенно зависит от распределения огибающей (t) входного процесса. Обозначив дисперсию входного процесса ², на основе выражений (5.10) и (5.13) получим . При чисто гармоническом входном сигнале ((t) = const, (t) = const), получим , а при входном процессе, соответствующем стационарному гауссову шуму с рэлеевским распределением ампдитуды вида (5.18), найдем . Таким образом, КПД генератора гармоник (по любой гармонике) при гауссовом возбуждении в n! раз больше, чем при гармоническом.

2. Корреляционные функции на выходе генератора гармоник

Рассмотрим спектральную плотность G_m(j) гармоники с номером m сигнала на выходе генератора гармоник. В соответствии с выражениями (4.5) и (6.5) получим:

.

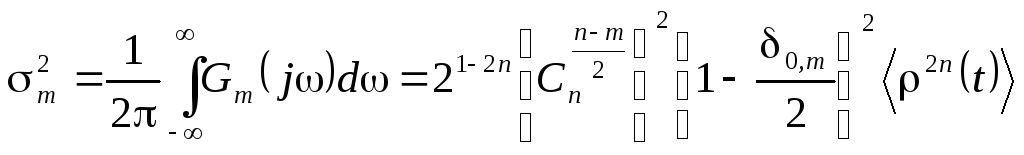Если входной процесс (6.2) является узкополосным, стационарным и гауссовым с корреляционной функцией B() = ²R(), то корреляционная функция выходного процесса B_() = <_> может быть представлена в виде ряда по степеням R():

(6.6)

Здесь

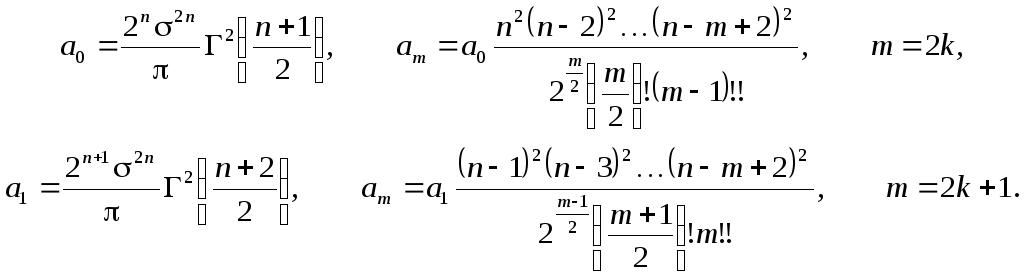
В соответствии с выражением (5.14), коэффициент корреляции узкополосного случайного процесса можно представить в виде

.

(6.7)

Используя выражение (6.4) при четном k можно записать:

.

Подставляя это выражение в формулу (6.6), получим

(6.8)

где

.

Для нечетных степеней k получается выражение, аналогичное (6.8), только суммы в нем ведутся по m = 1, 3, … , n. Сравнивая выражения (6.7) и (6.8), можно сделать вывод, что автокорреляционная функция гармоники с номером m определяется формулой

.

(6.9)

Взяв преобразование Фурье от полученного выражения, можно найти спектральную плотность интенсивности гармоники с номером m. Если спектр входного процесса симметричен относительно частоты ₀, второй множитель в выражении (6.7) равен нулю q() = 0. Тогда Q() = p()/2 – вещественная функция, входящая в формулу (6.8) величина

,

а функция Q_m() – вещественная и четная (поскольку p() = p(–)). Таким образом, спектральная плотность интенсивности m-й гармоники также симметрична относительно частоты m₀.

В качестве примера рассмотрим генерацию высшей гармоники n₀ (m = n), считая спектр входного процесса симметричным относительно ₀. В этом случае в сумме (6.8) останется только один член, а из выражения (6.9) следует:

.

Поскольку автокрреляционная функция процесса (6.2) с симметричным спектром определяется выражением (5.16), для спектральной плотности входного процесса и высшей гармоники получаем

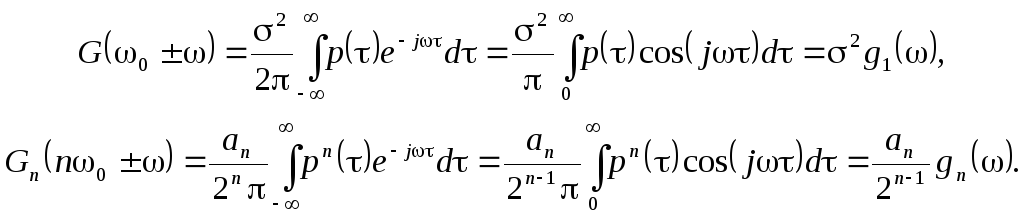
Введенные здесь функции g_i() определяются выражением:

.

Например, если функция p() имеет вид

,

получим

.

Таким образом, если спектральная плотность интенсивности процесса на входе генератора гармоник имеет форму лоренцевой кривой, спектр высшей гармоники также будет иметь лоренцеву форму, но в n раз шире.

Аналогично при

,

получим

.

Видно, что если спектр входного процесса гауссов, то спектр высшей гармоники тоже гауссов, но в данном случае уширение составляет раз.