3. Случайные функции 34

3. Случайные функции

Понятие случайной функции является обобщением понятий случайной величины и функции случайной величины. Случайной функцией (t) с параметром t называется функция, значение которой _i = (t_i) при любом значении параметра t = t_i является случайной величиной. Если параметр t имеет смысл времени, случайная функция называется случайным процессом, если координаты – случайным полем.

1. Задание случайной функции

В первом разделе мы вводили понятие случайной величины как результата некоторого эксперимента, который не воспроизводится при повторении этого эксперимента в тех же условиях. Однако, существует и другой подход, который заключается в представлении совокупности множества абсолютно идентичных систем, находящихся в абсолютно одинаковых условиях. Тогда при регистрации какой-либо характеристики системы одинаковыми способами получаемые значения (реализации) будут различными. Совокупность всех возможных реализаций называют статистическим ансамблем или ансамблем реализаций; соответственно, совокупность систем называют ансамблем систем.

Согласно данному нами в начале этого раздела определению случайной функции, функция случайной величины является случайной функцией; однако понятие случайной функции гораздо шире. Значения случайной функции (t) могут быть как непрерывными, так и дискретными; параметр t также может быть дискретным – в этом случае величина [n] = (t = t_n) называется случайной последовательностью.

Если параметр случайной функции принимает конечное число значений t₁,…, t_n, случайная функция эквивалентна совокупности случайных величин [1] = (t₁),…, [n] = (t_n), которая может быть описана n-мерной совместной функцией плотности вероятности (x₁,…, x_n). Однако, ситуация существенно осложняется, если количество значений аргумента бесконечно, либо аргумент непрерывен – в этом случае уже нельзя задать какую-либо функцию распределения и необходимо определить, как понимать задание случайной функции.

Если случайная функция (t) задана как статистический ансамбль своих реализаций, можно задать распределение вероятностей этих реализаций. Так, например, для счетного набора реализаций x⁽ⁱ⁾(t) можно ввести вероятности p_i каждой реализации и определить среднее по статистическому ансамблю:

.

Однако, обычно удобнее другой подход, основанный на представлении случайной функции (t) в произвольный момент времени в виде случайной величины, которая может быть задана с помощью одномерного распределения, зависящего от времени:

.

Тогда среднее по ансамблю находится как

.

Однако, следует понимать, что такое распределение никак не учитывает взаимосвязь значений (t) в разные моменты времени. Если задать n моментов времени t₁,…, t_n, можно ввести n-мерное распределение

.

Для конечной случайной последовательности такое описание будет полным. В общем случае говорят, что случайная функция задана, если ее конечномерное распределение _n(t₁,x₁,…, t_n,x_n) известно для любого числа n произвольно выбранных моментов времени t₁,…,t_n. Очевидно, функция плотности вероятности _n(t₁,x₁,…, t_n,x_n) должна быть симметричной относительно перестановок пар аргументов (t_i,x_i). Кроме того, должно выполняться условие согласования, аналогичное (1.17):

.

(3.1)

Введенные в п. 1 понятия сходимости последовательности случайной величины позволяют ввести понятие непрерывности случайной функции. Случайная функция называется непрерывной в среднеквадратичном смысле, если

.

Этот предел часто обозначают следующим образом:

.

Случайная функция называется непрерывной по вероятности, если ее среднее арифметическое сходится к математическому ожиданию в каждый момент времени:

.

Наконец, случайная функция называется непрерывной почти наверняка, если

.

Существует сокращенное обозначение этого равенства:

.

Следует помнить, что непрерывность случайной функции (t) по вероятности не означает непрерывности ее значений x(t). Так, например, в рассмотренной в п. 2.2 задаче о дробовом шуме заряд, пришедший на анод, является дискретной величиной, но случайная функция q(t) непрерывна по вероятности, так как в силу наших предположений вероятность прихода на анод одного электрона за время dt непрерывно уменьшается при уменьшении dt. Это означает, что

для любых  и . Это и означает непрерывность по вероятности.

По аналогии с понятием непрерывности определяется и дифференцируемость случайной функции – как существование в каком-либо смысле предела приращения функции к приращению аргумента

.

Интегрируемость случайной функции определяется как существование в каком-либо смысле предела частичных сумм

.

Случайная функция называется стационарной или однородной по времени, если для всех ее конечномерных распределений и для любого  выполняется равенство

.

(3.2)

Из этого определения, в частности, следует, что одномерная функция распределения стационарной случайной функции вообще не зависит от t, а n-мерная – зависит от n – 1 момента времени.

2. Моменты случайных функций

Моменты случайной функции определяются так же, как и моменты случайной величины. Например, момент n-го порядка определяется как

.

Смешанные моменты случайной функции могут быть построены но основе самых различных комбинаций ее значений, взятых в различные моменты времени. Например:

,

.

Смешанный момент второго порядка носит название корреляционной функции и имеет вид

.

(3.3)

Очевидно, при t₁ = t₂ = t B(t,t) = <²(t)>.

Центральный смешанный момент второго порядка

при t₁ = t₂ = t равен дисперсии случайной функции (t,t) = D[(t)]. Нормируя его, получим коэффициент корреляции:

.

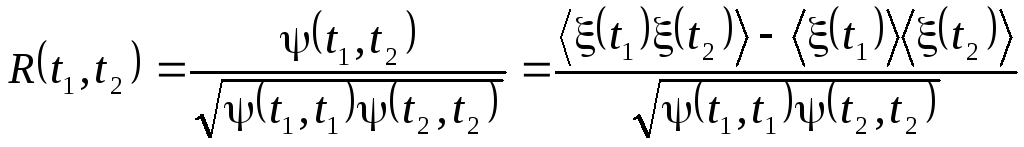Легко показать, что |R(t₁,t₂)|  R(t,t) = 1, а если значения (t₁) и (t₂) статистически независимы, то R(t₁,t₂) = 0.

Для случайных функций, так же, как и для случайных величин, можно ввести условную функцию распределения, например

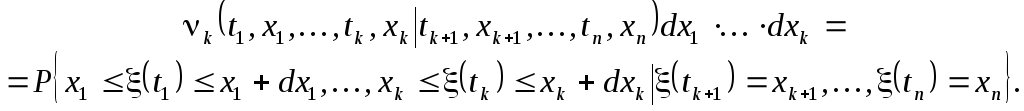
Тогда по аналогии с выражением (1.18) можно записать:

.

(3.4)

Для случайной функции можно ввести и условные моменты, например, условное среднее:

.

(3.5)

Пользуясь выражениями (3.4) и (3.5) корреляционную функцию (3.3) можно записать в виде

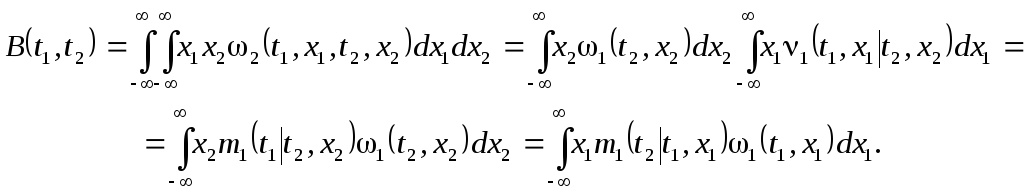
Следует отметить, что корреляционная функция является одной из важнейших характеристик случайного процесса. Существует даже корреляционная теория случайных процессов, которая оперирует моментами и функциями распределения только первого и второго порядков.

Поскольку для стационарных случайных процессов одномерная функция плотности вероятности не должна зависеть от времени, моменты n-го порядка таких процессов являются постоянными величинами:

.

Соответственно, функция корреляции стационарного случайного процесса зависит только от временного сдвига:

.

Ясно также, что и функция корреляции, и центральный смешанный момент второго порядка (), и нормированный коэффициент корреляции R() должны быть четными функциями временного сдвига, то есть

.

В рамках корреляционной теории обычно используют более широкое определение стационарности, по сравнению с данным нами определением в конце п. 3.1. на основе равенства (3.2). Стационарной в широком смысле или стационарной по Хинчину называют случайную функцию, функция корреляции которой зависит только от временного сдвига  = t₂ – t₁ и конечна при  = 0.

3. Эргодические случайные процессы

Введенные нами в начале данного раздела функции плотности вероятности (t,x), а также различные моменты определяются как средние по ансамблю. Однако на практике, обычно, приходится иметь дело с одной системой, которую можно наблюдать в течение какого-либо времени. При этом можно найти среднее по времени

,

которое, в свою очередь, также является случайной величиной. При этом

.

Предположим, что (t) – стационарный случайный процесс. Тогда средние величин (t) и совпадают и равны некоторой постоянной величине:

.

Найдем дисперсию среднего по времени:

Рис. 3.1. Замена переменных при вычислении дисперсии среднего

Осуществим в последнем интеграле замену переменных ₁ = ₂ – ₁ и ₂ = ₂ + ₁, эквивалентную повороту осей ₁ и ₂ на угол /4 (при этом, очевидно, ₁ = (₂ – ₁)/2 и ₂ = (₂ + ₁)/2). Разобьем площадь, на которой осуществляется интегрирование, на два треугольника, как это показано на рис. 3.1. Получим:

.

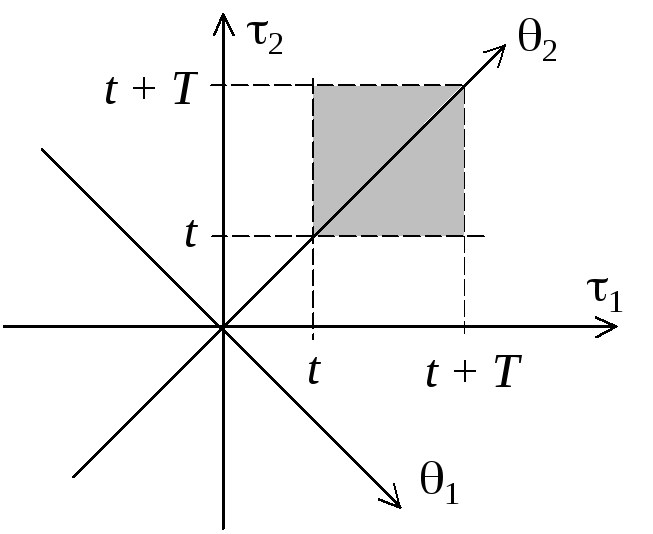
(3.6)

Теперь запишем неравенство Чебышева (1.13) для случайной величины :

.

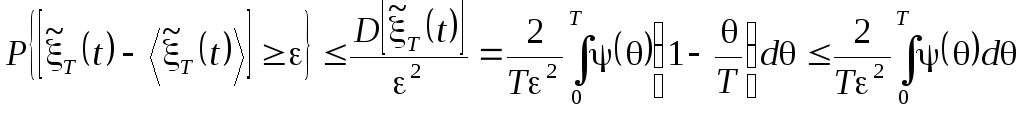Таким образом, если выполняется условие

,

(3.7)

то величина сходится по вероятности к статистическому среднему при T  , то есть

.

(3.8)

Условие (3.7) называется условием эргодичности Слуцкого для стационарных случайных процессов, а удовлетворяющие ему или выражению (3.8) случайные процессы называют эргодическими.
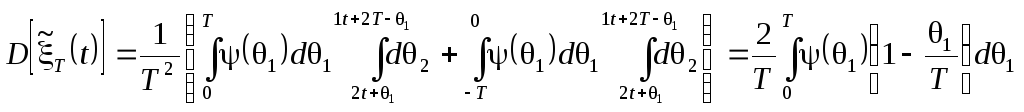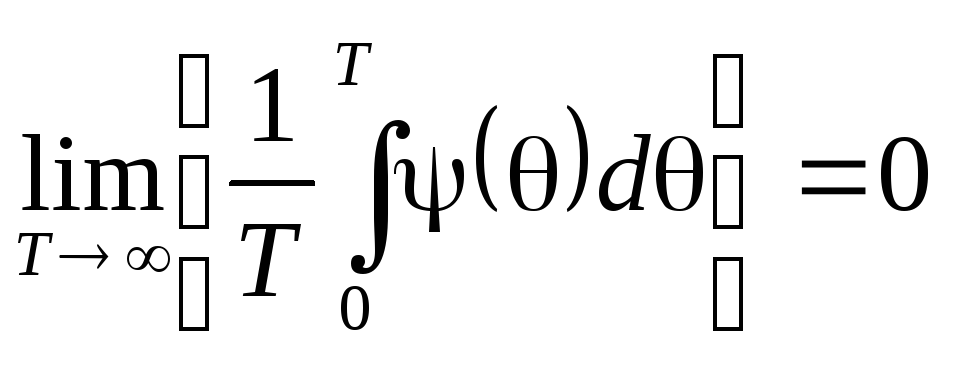