1. Основы теории вероятностей 18

1. Основы теории вероятностей

Предметом теории вероятностей являются массовые явления – длинные серии экспериментов при определенном комплексе условий. Если при воспроизведении данного комплекса условий результаты экспериментов также воспроизводятся, процесс называют детерминированным. В противном случае процесс являетсяслучайным. Вопрос о том, можно ли путем учета и воспроизведения всех условий превратить случайный процесс в детерминированный тесно связан с квантовомеханическим соотношением неопределенности и до сих пор является открытым.

1. Понятие вероятности. Аксиома измерений

Каждому результату эксперимента можно поставить в соответствие некоторую величину илисобытие. Так, например, при измерении напряжения некоторого источника величиной является измеренное напряжение, а событием – попадание этого напряжения в некоторый заранее заданный интервал.

Если в серии из Nэкспериментов, выполняющихся при определенном комплексе условий, событиеAпроизошлоnраз, то=n/N–частота появлениясобытияAвNэкспериментах. Ясно, что тот факт, что приNэкспериментахnраз произойдет событиеA, также является случайным событием, а частота появления– случайной величиной. Однако в любой достаточно длинной серии экспериментов частота появления является устойчивой величиной, которая приNстремится к некоторому значению₀. Этот факт является статистической закономерностью; именно такие закономерности и являются предметом изучения теории вероятностей и статистической радиофизики.

Введем вероятность случайного события Aкак величину, мало отличающуюся отпри большихN. Утверждение, заключающееся в том, что для каждого случайного событияAсуществует его определенная вероятностьp=P{A} означает, что в любых достаточно длинных сериях экспериментов частоты появления событияAбудут приблизительно одинаковы и близки к величинеp. Само по себе существование величиныpдля широкого класса массовых явления подтверждается практикой и является основой теории вероятностей. Предположение

(1.1)

называется аксиомой измерения. Ясно, что 0P{A}1.

Для двух взаимосвязанных событий можно ввести условную вероятность P{A|B}, то есть вероятность возникновения событияAпри условии, что произошло событиеB. Из частотного определения вероятности следует, что

P{A|B} =P{AB}/P{B},P{B|A} =P{AB}/P{A}

(1.2)

Отсюда

.

(1.3)

Безусловные вероятности P{A} часто называютаприорными, а условныеP{A|B} –апостериорными. Если событияAиBнезависимы, то в соответствии с (1.2)P{A|B} =P{A},P{B|A} =P{B}, то есть

P{AB} =P{A}P{B}.

Если есть Kвзаимно независимых событийA₁…A_K, причем вероятностьP{A₁+A₂+ … +A_K} = 1, то есть имеется полная группа изKгипотез, то

.

(1.4)

Мы получили формулу полной вероятности. На ее основе с использованием выражения (1.3) можно записатьформулу Байеса:

.

(1.5)

2. Случайные величины. Распределение вероятностей

Рассмотрим непрерывную или дискретную случайную величину как результат некоторого эксперимента и поставим ей в соответствие множество случайных событий, заключающихся в том, что=x_i (для дискретной величины) илиx<<x+x(для непрерывной величины). Закон по которому каждому значениюx_i(или интервалуx) ставится в соответствие вероятность того, чтопримет это значение (попадет в этот интервал), называютзаконом распределениявероятности случайной величины. Аналитическим выражением закона распределения являетсяфункция распределения. Введеминтегральную функцию распределениякакF(x) =P{x} и сформулируем ряд ее очевидных свойств:F(–) = 0,F() = 1,F(x₁)F(x₂) еслиx₁x₂.

Если интегральная функция распределения случайной величины непрерывна и дифференцируема, то случайную величину называют непрерывной, а производную интегральной функции распределения

(1.6)

называют функцией плотности вероятности. Ясно, что

.

Можно ввести функцию плотности вероятности и для дискретной случайной величины. Если p_i=P{=x_i}, то

.

Определим среднее значение произвольной функции случайной величины f() как

для непрерывной величины и

для дискретной. Для любой случайной величины можно ввести моментыn-го порядка, которые определяются как среднее отⁿ. Для непрерывной и дискретной случайных величин моментn-го порядка равен соответственно

.

(1.7)

Среднее или первый момент случайной величины называется математическим ожиданием:.

В статистической радиофизике используют также центральные моменты:

.

Центральный момент второго порядка называется дисперсией:

.

.

(1.8)

Рассмотрим ряд примеров распределений случайных величин. Пусть эксперимент может иметь только два исхода – либо происходит событие Aс вероятностьюP{A} =p, либо событиеBс вероятностьюP{B}=q= 1 –p. Тогда вероятность того, что приNиспытанияхnраз произойдет событиеAопределяетсябиноминальным законом распределения:

.

(1.9)

Найдем моменты этого распределения:

Теперь можно найти первый и второй моменты:

,

,

а также дисперсию, пользуясь выражением (1.8):

.

Вид биноминального закона распределения (1.9) при p= 0,1 и различных значенияхNпоказан на рис. 1.1.

Будем увеличивать число испытаний Nтак, чтобы произведениеNp=m₁= <n> оставалось постоянным (вероятностьpпри этом будет уменьшаться). Сделаем ряд преобразований выражения (1.9):

Поскольку известно, что

,

Рис. 1.1. Биноминальный закон распределения

получим

–

(1.10)

распределение Пуассона(рис. 1.2). Вычисление моментов этого распределения дает:

Рис. 1.2. Распределение Пуассона

.

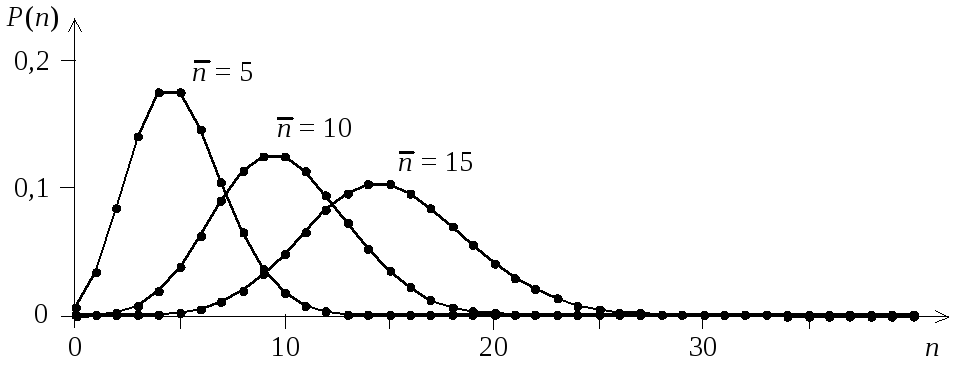
Формулы для первых двух моментов и дисперсии распределения Пуассона имеют вид:

,

,

.

Рис. 1.3. Распределение Муавра-Лапласа

Совершенно аналогично рассмотрим другой предельный переход распределения (1.9) – устремим Nк бесконечности при постоянной вероятностиp=const(p0 иp1). Получим

–

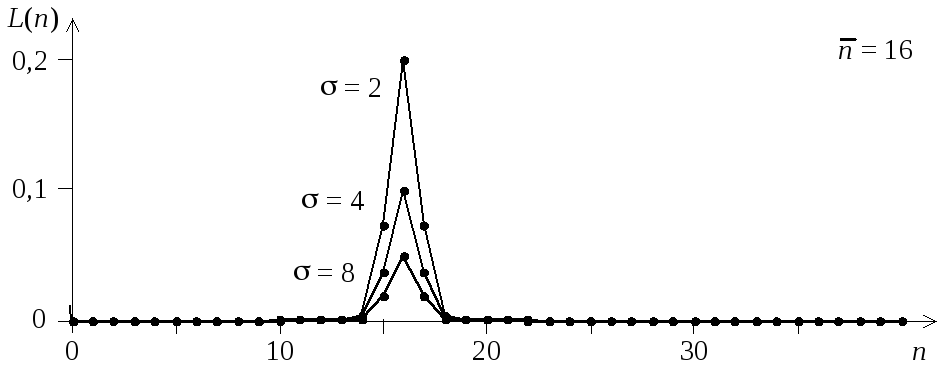
(1.11)

распределение Муавра-Лапласа(рис. 1.3), где,. При больших значенияхnможно пренебречь дискретностью и отnперейти к непрерывной величинес функцией плотности вероятности вида

.

(1.12)

Эта функция описывает нормальное распределение(распределение Гаусса), для которого,. Вид распределения Гаусса показан на рис. 1.4.

3. З

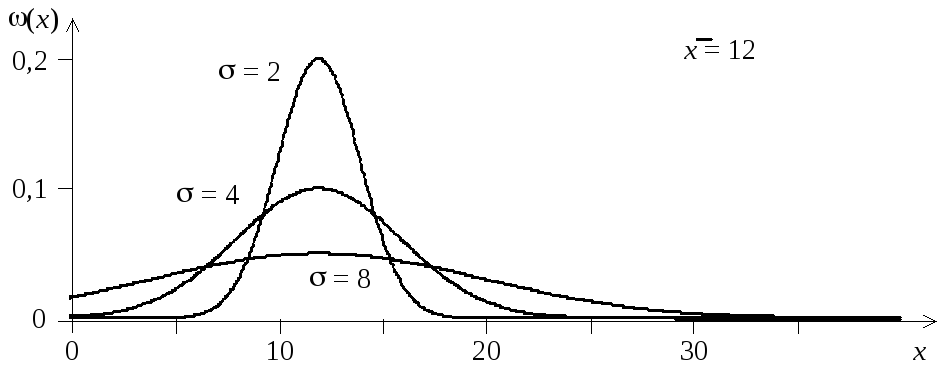
Рис. 1.4. Распределение Гаусса