5. Воздействие случайных процессов на линейные системы 55

5. Воздействие случайных процессов на линейные системы

В данном разделе мы рассмотрим прохождение случайного процесса через линейную систему и получим выражения, связывающие спектральные характеристики процессов на входе и выходе системы, а также найдем распределение вероятностей на выходе. Здесь же будет рассмотрено прохождение через систему узкополосного гауссового процесса.

1. Спектр процесса на выходе линейной системы

Рассмотрим систему, связь между входным x(t) и выходнымy(t) сигналами которой описывается линейным дифференциальным уравнением вида

.

Известно, что реакция такой системы на произвольное входное воздействие может быть найдена с помощью интеграла Дюамеля:

.

Здесь h(t) – импульсная характеристика системы, равная нулю при t< 0,x(t) – начавшийся в момент времениt = 0 входной сигнал. Для входного сигнала, начавшегося бесконечно давно, выражение (5.1) примет вид

.

(5.1)

Рассмотрим в качестве входного сигнала стационарный случайный процесс ₁(t). Поскольку любая физически реализуемая цепь имеет конечное время установления (релаксации)_р, можно считать, чтоh(>_р) = 0 и записать выражение для средних значений процессов на входе₁(t) и выходе₂(t) системы:

.

(5.2)

Таким образом, выходной случайный процесс ₂(t) также стационарен. Найдем его функцию автокорреляцииB₂():

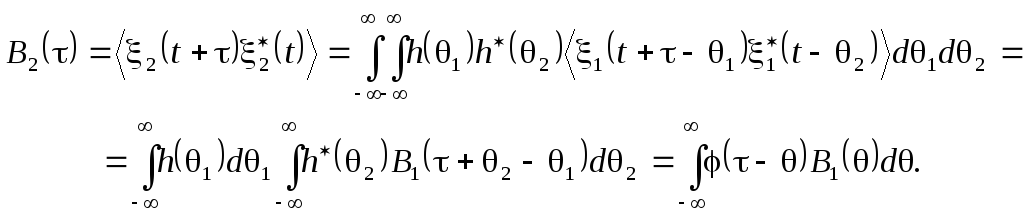
Здесь введены обозначения

.

Используя выражения (4.3) и (4.4), получим выражение для спектральной плотности интенсивности процесса на выходе:

Осуществляя в интеграле по dзамену–=и подставляя явный вид функции(), получим:

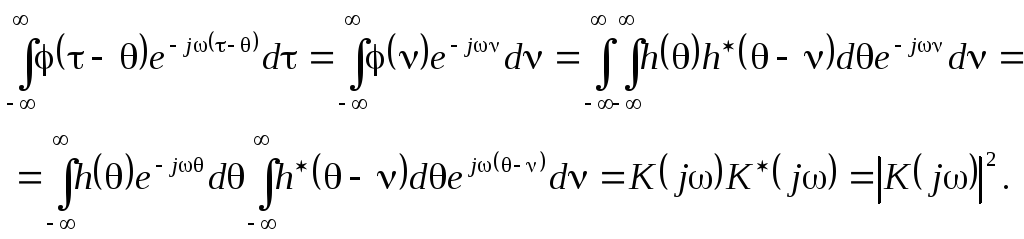
Здесь

–

частотная характеристика системы. Подставляя полученный результат в выражение для G₂(j) и учитывая, что

,

получим:

.

Мы нашли связь между спектральными плотностями интенсивности входного и выходного процессов:

.

(5.3)

Полученное выражение (5.3) позволяет не только найти спектральную плотность интенсивности процесса на выходе линейной системы, но и определить физический смысл этой функции. Рассмотрим в качестве системы узкополосный фильтр, частотная характеристика которого имеет вид

причем будем считать, что ширина полосы пропускания фильтра настолько мала, что в ее пределах можно считатьG₁(j) =G₁(j₀) =const. Тогда средний квадрат шума на выходе фильтра равен

.

Таким образом, спектральная плотность интенсивности процесса на частоте ₀– это энергия данного процесса, приходящаяся на единичную полосу частот вблизи₀.

Вместе с теоремой Винера-Хинчина (4.4) выражение (5.3) позволяет записать функцию автокорреляции процесса на выходе системы:

.

(5.4)

2. Р

3. 5.2 Распределение вероятностей на выходе линейной системы

Рассмотрим линейную систему, на вход которой подан стационарный гауссов процесс, представимый в виде , причем, то есть. Поскольку все моменты стационарного процесса постоянны, его двумерное совместное распределение можно записать в виде (1.21):

,

(5.5)

где

.

Естественно, любое одномерное распределение гауссова процесса должно удовлетворять нормальному закону:

.

(5.6)

Случайный процесс на выходе нашей системы можно записать в виде интеграла Дюамеля (5.1):

.

Поскольку в этой сумме все слагаемые ₁(nt) имеют нормальное распределение вида (5.6), их сумма, взятая с любыми весами, (то есть₂(t)) также будет распределена нормально, но с другими моментами. С учетом выражений (5.2) и (5.4), запишем:

, ,.

Таким образом, распределение случайного процесса на выходе является нормальным, но с другими параметрами.

Рассмотрим другой случай – процесс на входе системы не является нормальным, однако для него система может считаться узкополосной, то есть <<_G, где– полоса пропускания системы, а_G– полоса частот, гдеG₁(j)0. На основе соотношения неопределенности (4.8) можно утверждать, что при таких условиях интервал корреляции входного процесса₁будет существенно меньше времени релаксации системы_р:₁<<_р. Выберем временной интервалтак, чтобы выполнялось условие₁<<<<_ри перепишем интеграл Дюамеля (5.1) в виде

,

где ,,N=_р/>> 1. Поскольку>>₁, можно считать, что величины_nнекоррелированы, а выходной процесс₂(t) является суммой большого числа некоррелированных случайных величин; тогда в силу центральной предельной теоремы он является нормальным процессом. Таким образом, при прохождении через узкополосную систему любой стационарный случайный процесс нормализуется – в этом состоит суть так называемойтеоремы о нормализации.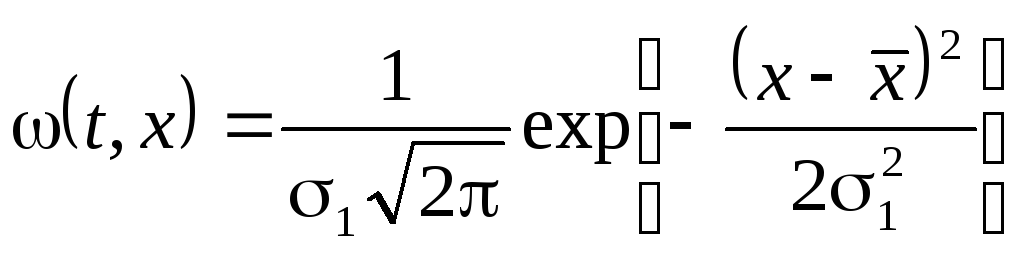